На рынке обращаются различные рисковые активы, такие как акции, облигации, паевые инвестиционные фонды и другие, с помощью которых можно создать такой портфель из финансовых активов, который будет приносить максимальную доходность при минимальном риске. Неопределенность, характерная для финансовых рынков, требует от инвестора рационального подхода при построении стратегии управления портфелем и умения управлением риском. Одним из средств уменьшения риска является диверсификация портфеля. Широкое применение в этой области нашли модели финансовых рынков, состоящих из рисковых и безрисковых активов. Одной из таких моделей является модель САРМ.
Модель САРМ (модель оценки доходности финансового актива) позволяет связать доходность актива с его риском. Вычислив ожидаемую доходность актива, можно рассчитать его внутреннюю стоимость. Поэтому модель САРМ называют также моделью ценообразования финансовых активов [4].
Модель CAPM описывается двумя уравнениями:
1. Первое исходное уравнение CAPM представляет зависимость между ожидаемой доходностью вложений инвестора и риском, т. е.
μV= i + (μМ — i)* σV/σM,
где μV — это ожидаемая доходность вложений инвестора; σV — стандартное отклонение вложений инвестора; μМ — это ожидаемая доходность рыночного портфеля М; σM- стандартное отклонение рыночного портфеля М.
Оно представляет собой линию CML (CapitalMarketLine — линия рынка капитала). На этой линии располагаются только эффективные портфели, неэффективные портфели располагаются ниже линии СML. Линия CML используется на практике только для широко диверсифицированных портфелей.
2. Второе уравнение модели определяет зависимость между ожидаемой доходностью отдельного рискового актива и коэффициентом его рыночного риска, т. е. μFи βF.
μF= i + (μM — i)* βF,
где μF — ожидаемая доходность отдельного рискового актива F;βF — коэффициент чувствительности к рыночному портфелю.
На линии SML располагаются абсолютно все активы, как эффективные портфели, так и неэффективные портфели, и отдельные рисковые активы.
Угол наклона линии SML показывает, сколько премии за рыночный риск приходится на единицу коэффициента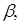
т. е. в какой степени рынок компенсирует инвестору величину рыночного риска отдельного актива. Величина компенсации зависит от общих условий рыночной конъюнктуры. При благоприятной рыночной обстановке угол наклона меньше, т. е. линия SML более пологая.
Сформировав широко диверсифицированный портфель, инвестор может снизить общий риск до уровня рыночного риска. В соответствии с допущениями модели CAPM (отсутствие трансакционных издержек), диверсификация портфеля должна осуществляться без увеличения затрат на формирование портфеля. Поэтому в модели CAPM компенсируется только рыночный риск, т. к. нерыночный риск можно снизить за счет диверсификации.
Модель CAPM имеет много ограничений:
1) наличие эффективного рынка — это рынок, на котором нет препятствий для распространения информации;
2) активы обладают достаточно высокой ликвидностью и однородностью;
3) отсутствие трансакционных издержек;
4) инвесторы являются рационально действующими и имеют одинаковые ожидания относительно характеристик рынка;
5) инвесторы имеют возможность заимствовать и предоставлять свои средства по безрисковой ставке;
6) рассматривают короткий период действия модели (модель одного временного периода).
Таким образом, модель САРМ имеет много допущений не выполнимых в действительности. Однако, несмотря на недостатки модели САРМ, ее широко применяют на практике. Например, с помощью нее инвестиционные компании рассчитывают аналитические коэффициенты Трейнора и Шарпа, а также показатель «альфа» — для определения недооцененных финансовых активов.
Согласно САРМ цена актива будет изменяться до тех пор, пока он не окажется на линии SML. Фонды размещаются в координатах «бета — средняя доходность», далее проводится прямая, проходящая через точки, соответствующие безрисковой доходности и доходности рынка. В качестве показателя рынка берутся индексы. Фонды, лежащие над прямой, более эффективны, чем рынок, под прямой — менее эффективны.
На практике можно обнаружить активы, которые неверно оценены рынком относительно равновесной ожидаемой доходности. Если актив неверно оценен рынком, т. е. его оценка не соответствует реальному инвестиционному качеству актива, то в следующий момент рынок заметит это и изменит свою оценку в направлении более объективной оценки. В результате мнение рынка будет стремиться к некоторому равновесному уровню доходности. В этом случае актив окажется на линии SML [1, c. 81].
Из САРМ следует, что рыночный портфель М, объединяющий рисковые активы, является эффективным (лежит на линии CML). Тогда для получения эффективного портфеля, лежащего на линии CML, можно использовать стратегию индексирования, то есть создать портфель, включающий в себя ценные бумаги в таких же пропорциях, как и рыночный портфель М [1, c. 82].
Рассмотрим следующую практическую задачу, позволяющую, используя модель САРМ, превзойти рынок [2].
На фондовом рынке РФ обращается недооцененный (α>0 по линии SML) актив — ОПИФ акций «Сбербанк — Финансовый сектор» [3], который не является эффективным (лежит ниже линии CML). В этом случае данный актив следует объединить с рыночным портфелем. В качестве рыночного портфеля можно рассмотреть индексный фонд — «Солид — Индекс ММВБ» [3], который хорошо отражает структуру рыночного индекса, т. е. приближен к рыночному индексу. Полученный портфель следует объединить с безрисковыми бумагами. На самом деле каждая из ценных бумаг обладает определенным риском, однако некоторые из них имеют незначительный риск. Показатель доходности по таким бумагам будем использовать для оценки безрисковой доходности. В этих целях воспользуемся доходностью ОПИФ «Сбербанк — Фонд денежного рынка» [3]. Данная стратегия позволит превзойти рынок, т. е. можно получить такие комбинации, которые лежат выше линии CML, и, тем самым, сформировать эффективный комбинированный продукт на фондовом рынке РФ.
Исходные данные: Рассматриваются ежедневные данные цен финансовых активов ОПИФ акций «Сбербанк — Финансовый сектор» (обозначим F), «Солид — Индекс ММВБ» (обозначим M) за временной промежуток с 5 ноября 2014 г. по 30 апреля 2015 г. В качестве источника данных о котировках финансовых инструментов был использован информационный портал «Investfunds» [3]. На основе информации о ценах рассчитываются доходности финансовых инструментов (ОПИФ акций «Сбербанк — Финансовый сектор», «Солид — Индекс ММВБ») по формуле:
,
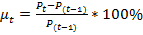где Pt–цена в нынешний период; P(t-1)- цена за предыдущий период,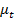
.– доходность в момент времени t.
Затем была рассчитана средняя доходность «Солид — Индекс ММВБ» по формуле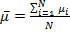 
,
и стандартные отклонения доходностей «Сбербанк — Финансовый сектор», «Солид — Индекс ММВБ» по следующей формуле:
,
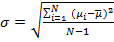где σ — стандартное отклонение доходности актива; µi–фактическая доходность актива в момент времени i;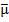 
– средняя доходность актива; N –количество наблюдений.
Далее рассчитывается коэффициент корреляции между доходностями ОПИФ акций «Сбербанк — Финансовый сектор» (F) и «Солид — Индекс ММВБ» (M) по формуле:
,
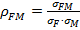где ρFM– коэффициент корреляции;σFM– ковариация доходностей активов F и M; σF, σM — стандартные отклонения доходностей активов F и M соответственно.
Далее вычисляется показатель «бета» по следующей формуле:
,
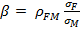где ρFM– корреляция доходностей активов F и M; σF– стандартное отклонение доходности актива F; σM- стандартное отклонение доходности актива M.
Затем рассматривается годовая доходность ОПИФ «Сбербанк — Фонд денежного рынка» [3]. На основе эквивалентности процентных ставок рассчитывается ежедневная доходность ОПИФ «Сбербанк — Фонд денежного рынка» по следующей формуле:
1+ j = (1+ j365/365)365,
где j — годовая процентная ставка, начисляемая один раз в год, j365– годовая процентная ставка, начисляемая каждый день, i= j365/365 — ежедневная доходность.
Далее вычисляется показатель «альфа» для ОПИФ акций «Сбербанк — Финансовый сектор» по формуле:
α = µф — µт,
где µф - фактическая средняя доходность актива; µт- теоретическая ожидаемая доходность актива.
В итоге имеем следующие исходные данные, на основании которых будет показана стратегия, как превзойти рынок.
Таблица 1
Исходные данные
|
Показатель |
Обозначение |
Значение показателя |
|
Безрисковая ставка (% за день) |
i |
0,0229 |
|
Стандартное отклонение доходности «Солид — Индекс ММВБ» (% за день) |
σм |
1,6994 |
|
Стандартное отклонение доходности «Сбербанк — Финансовый сектор» (% за день) |
σF |
1,8915 |
|
Средняя доходность «Солид — Индекс ММВБ» |
μM |
0,1279 |
|
альфа (% за день) |
α |
0,0381 |
|
коэффициент корреляции между доходностями «Сбербанк — Финансовый сектор» и «Солид — Индекс ММВБ» |
ρ |
0,5147 |
|
бета |
β |
0,5729 |
На основе исходных данных построим линии SML и СML.
На рисунке 1 изображен недооцененный пай — «Сбербанк — Финансовый сектор», который располагается над линией SML.
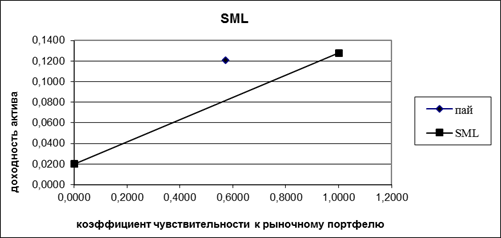
Рис. 1. Линия SML и недооцененный пай
При построении линии рынка капитала CML мы видим, что данный пай расположен под линией (см. рис. 2).
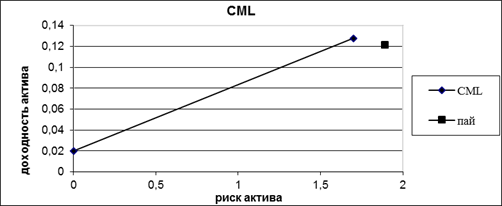
Рис. 2. Линия рынка капитала
Объединяем рыночный портфель и пай в один портфель P. На рисунке 3 изображены различные комбинации портфеля P(дуга) с учетом коэффициента корреляции.
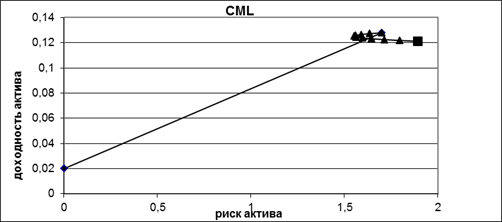
Рис.3. Объединение рыночного портфеля и пая
Проводим касательную к портфелю P(к дуге) из безрисковой ставки (см. рис. 4).
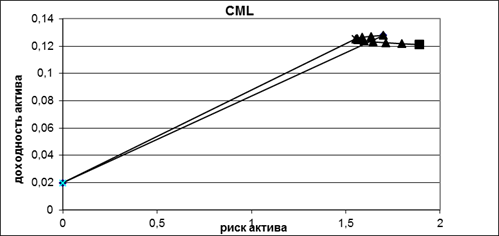
Рис. 4. Объединение пая с рыночным портфелем и безрисковой ставкой
На касательной находятся портфели, которые рекомендуются инвестору. Для определения структуры портфеля необходимо воспользоваться следующей математической моделью.
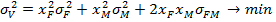
при следующих ограничениях:
xF+ xM+ xi= 1,
xi ≥ 0, xF≥ 0, xM≥ 0,
μV=xFµF+ xMµM+ xii≥ R,
где xF, xM, xi– доли активов «Сбербанк — Финансовый сектор», «Солид — Индекс ММВБ» и «Сбербанк — Фонд денежного рынка» соответственно в общем объеме вложений инвестора, μV — ожидаемая доходность вложений инвестора,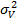 
— риск всех вложений инвестора, 
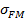– ковариация между доходностями активов «Сбербанк — Финансовый сектор» и«Солид — Индекс ММВБ», R — фиксированный уровень доходности (задается в зависимости от предпочтений инвестораотносительно доходности и риска).
Данная математическая модель показывает, что при заданном уровне доходности, инвестор стремится минимизировать свои риски.
Итак, объединив недооцененный (α>0 по линии SML) актив — ОПИФ акций «Сбербанк — Финансовый сектор» (лежащий ниже линии CML) с индексным фондом — «Солид — Индекс ММВБ» и безрисковой ставкой ОПИФ «Сбербанк — Фонд денежного рынка», сформировали эффективные комбинированные продукты, лежащие выше линии CML. Таким образом, данная стратегия позволила превзойти рынок.
Литература:
1. Колясникова Е. Р. Прогнозирование показателей финансовых рынков: Учебно-практическое пособие. Уфа: РИЦ БашГУ, 2013. — 128 с.
2. Колясникова Е. Р., Козелова Т. А. Построение интегрированного продукта на фондовом рынке РФ // Молодой ученый. — 2014. — № 4 (63). — С. 537–539.
3. Информационное агентство «Cbonds.ru» [Электронный ресурс]. Электр.текстовые и графические дан.– М.: «Investfunds». Режим доступа: http://www.investfunds.ru/, свободный.
4. Студопедия [Электронный ресурс]. Модель САРМ. Режим доступа: http://studopedia.net/9_41033_v-model-sarm.html, свободный.
