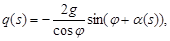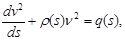Применение прямой задачи динамики к определению рабочей поверхности рыхлительной лапы

Закон движения почвенной частицы по рабочей поверхности рыхлительной лапы имеет вид s=f(t);                                                                                                                                         (1)

здесь f(t)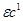, причем f(t) строго возрастает. Отсюда следует, что равенство (1) разрешимо относительно t,т. е. t=g(s),                                                                                                      (2)

где g—обратная к f функция; при этом 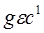                                                         (3)

на основании теоремы о дифференцируемоети обратной функции. В силу (2) соотношение v — v(t) преобразуется следующим образом:

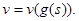                        (4)

Отсюда вытекает, что линейная скорость v почвенного комка при его движении по рабочей поверхности представима и в виде функции криволинейной абсциссы s. Там, где это не может стать причиной неясности, будем писать v(s) вместо правой части (3) и под v подразумевать v(s), если аргументом служит s. Из (5), (3), (4) и теоремы о производной сложной функции следует, что 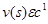, причем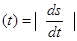

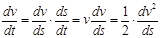                                                                                               (5)

на основании (5) система дифференциальное уравнение равносильна

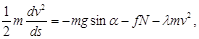                                                                                     (6)

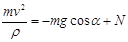                                                                                                       (7)

где аргументом каждой функции служит s. В случае прямой задач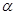и и 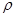заданы, следовательно, неизвестными в системе (6)... (7) являются v и N. Образуя линейную комбинацию уравнений (6) и (7) с коэффициентами 1 и f, получим дифференциальное уравнение первого порядка

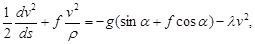                                                                       (8)

содержащее только искомую функцию v. Чтобы привести ого к нормальной форме, введем угол трения почвы о рабочую поверхность рыхлительной лапы. Обозначим его величину через 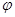. Тогда 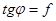.                                                                                                                                    (9)

В силу (9)

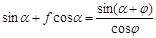.                                                                                               (10)

На основании (10) уравнение (8) примет вид

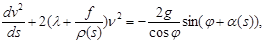                                                                     (11)

В уравнение (11) входят, помимо 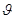, только функци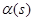и ) и 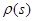, однозначно определяемые заданием направляющей лини; оно содержит также, кроме g, лишь постоянные f, 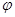=arctg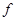и 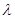, с помощью которых описываются силы сопротивления перемещению комков почвы. Отсюда следует, что распределение линейных скоростей почвенны частиц, перемещающихся по рабочей поверхности рыхлительной лапы во время выполняемого ею рабочего процесса, зависит только от формы этой поверхности, и параметров, характеризующих диссипацию энергии движущихся частиц.

Соотношение (1) — линейное относительно 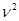 дифференциальное уравнение первого порядка. Для упрощения записей положим

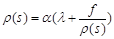                                                                                                          (12)

                                                                                            (13)

Тогда равенство (11) примет форму

                                                                                                        (14)

Чтобы установить начальное условие, которому удовлетворяет функция v(s) при s=0, примем во внимание следующее из условий квазистационарности следует, что до соударения с поверхностью S скорость почвенной частицы в системе координат К равна -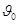; вектор v₀ компланарен плоскости направляющей L. При столкновении комка с рабочей поверхностью S нормальная к S составляющая его скорости относительно лапы обращается в нуль, а касательная к S и, следовательно, к линии L составляющая сохраняется, становясь начальной скоростью ого дальнейшего движения. Поэтому

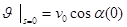                                                                                                       (15)

следовательно, ввиду неотрицательности обеих частей (15)

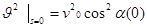.                                                                                                 (16)

Решение линейного дифференциального уравнения

Y'+p(x)y = q(x)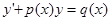,                                                                                  (17)

удовлетворяющее начальному условию

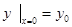                                                                                                                     (18)

И вытекает следующая общая формула для вычисления нормального давления почвы на рабочего поверхность рыхлительной лапы во время рабочего процесса

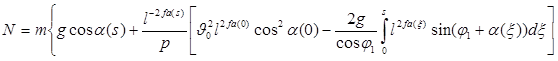  (19)

Литература:

1.         Байметов Р. И., Флайшер Н. М. Оптимизация параметров рабочих органов почвообрабатывающих машин. Тошкент 1991 г.