В статье разработан алгоритм и реализована программа решения задачи оптимального управления на основе метода вариаций. Реализованный алгоритм был апробирован на тестовых примерах.
Ключевые слова: метод вариаций, оптимальное управление, численное решение.
Введение. Задачи оптимального управления встречаются в различных сферах человеческой деятельности. Каждое разумное действие является в определенном смысле и оптимальным, ибо оно, как правило, выбирается после сравнения с другими вариантами. Интерес к задачам наилучшего выбора был высоким всегда, но особенно возрос в последние годы в связи с интенсивным развитием науки и техники. В связи с этим возникает проблема выбора из множества вариантов решения задачи того, который обеспечивает наилучшее или наиболее эффективное распределение ресурсов. Этот наилучший вариант и называется оптимальным. Выбор оптимального варианта определяется каким-либо показателем, который называется критерием оптимизации.
Постановка задачи. Пусть управляемый процесс представлен системой дифференциальных уравнений:
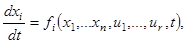 (1)
(1)
где 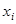 — фазовые переменные, а
— фазовые переменные, а 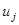 — переменные управления,
— переменные управления, 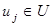 .
.
При 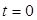 заданы все начальные значения фазовых переменных
заданы все начальные значения фазовых переменных 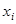 :
:
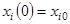 ,
, 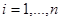 . (2)
. (2)
На управление и фазовые переменные наложены ограничения типа:
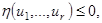
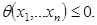 (3)
(3)
Область, ограниченную неравенством для управлений в пространстве переменных 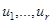 , будем называть допустимой областью
, будем называть допустимой областью 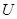 .
.
Критерий оптимизации пусть задан в терминальном виде:
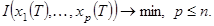 (4)
(4)
Требуется найти такое управление 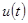 , удовлетворяющее условиям (3), чтобы величина
, удовлетворяющее условиям (3), чтобы величина 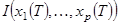 приняла минимальное значение.
приняла минимальное значение.
Для численного решения данной задачи был составлен алгоритм метода вариации в пространстве управлений:
1. Интегрируя систему (1) при 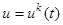 с начальными условиями (2) в интервале
с начальными условиями (2) в интервале 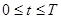 , вычисляем значение критерия I. Запоминаем значение критерия и управление в достаточном числе точек.
, вычисляем значение критерия I. Запоминаем значение критерия и управление в достаточном числе точек.
2. Варьируем управление по направлениям 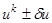 в точке
в точке 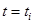 . Интегрируем систему (1) при
. Интегрируем систему (1) при 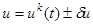 с начальными условиями (2) в интервале
с начальными условиями (2) в интервале 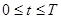 , вычисляем значение критерия I. Если критерий улучшился, и при этом выполняются условие (3), то запоминаем это значение критерия и управление в достаточном числе точек.
, вычисляем значение критерия I. Если критерий улучшился, и при этом выполняются условие (3), то запоминаем это значение критерия и управление в достаточном числе точек.
3. Переходим к следующей точке 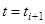 и выполняем п.2 со «старым» приближением
и выполняем п.2 со «старым» приближением 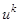 . После того, как пробежим все точки отрезка
. После того, как пробежим все точки отрезка 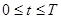 , переходим к
, переходим к 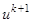 . Повторяем цикл до тех пор, пока не выполнится условие
. Повторяем цикл до тех пор, пока не выполнится условие 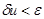 . Если критерий на отрезке
. Если критерий на отрезке 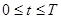 не улучшился, то уменьшаем вариацию вдвое, т. е.
не улучшился, то уменьшаем вариацию вдвое, т. е. 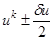 .
.
Тестирование алгоритма. На основе созданного алгоритма реализована программа. Рассмотрим работу полученного алгоритма на следующих примерах. Для вычисления погрешностей будем использовать евклидову норму:
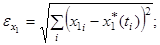
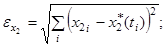
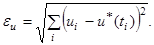
Пример 1. Допустим, что некоторый процесс описывается системой дифференциальных уравнений:
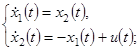 (5)
(5)
с начальными условиями:
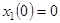 ,
, 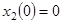 (6)
(6)
и следующими ограничениями на переменную времени:
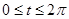 (7)
(7)
и на управление:
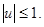 (8)
(8)
Критерий оптимизации имеет вид
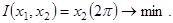 (9)
(9)
Требуется найти оптимальное программное управление 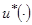 и соответствующую ему траекторию
и соответствующую ему траекторию 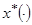 , которые удовлетворяют уравнениям (5)-(6), ограничениям (7)-(8) и условию (9).
, которые удовлетворяют уравнениям (5)-(6), ограничениям (7)-(8) и условию (9).
Аналитическое решение данной задачи представлено в [2].
На рис. 1 — рис. 2 изображено численное решение данной задачи, при начальном приближении 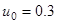 .
.
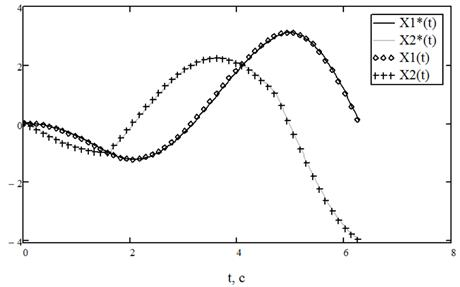
Рис. 1. Графики оптимальных траекторий для примера 1
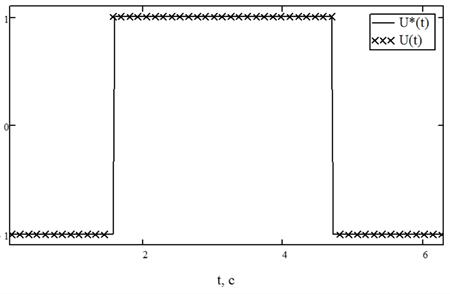
Рис. 2. График оптимального управления для примера 1
Сравнивая полученные численные и аналитические значения, вычислим погрешности для управления и траекторий.
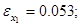
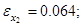
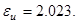
Пример 2. Пусть управляемый процесс описывается системой дифференциальных уравнений:
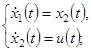 (10)
(10)
с начальными условиями:
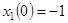 ,
,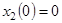 (11)
(11)
и следующими ограничениями на переменную времени:
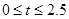 (12)
(12)
и на управление, фазовые переменные:
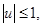
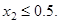 (13)
(13)
Критерий оптимизации имеет вид
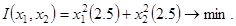 (14)
(14)
Требуется найти оптимальное программное управление 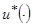 и соответствующую ему траекторию
и соответствующую ему траекторию 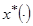 , которые удовлетворяют уравнениям (10)-(11), ограничениям (12)-(13) и условию (14).
, которые удовлетворяют уравнениям (10)-(11), ограничениям (12)-(13) и условию (14).
Аналитическое решение данной задачи представлено в [1].
На рис. 3 — рис. 4 изображено численное решение данной задачи, при начальном приближении 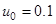 .
.
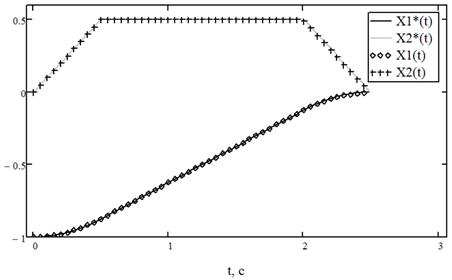
Рис. 3. Графики оптимальных траекторий для примера 2
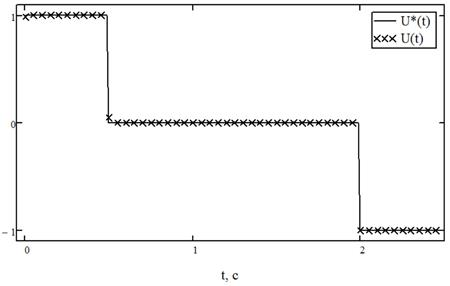
Рис. 4. График оптимального управления для примера 2
Сравнивая полученные численные и аналитические значения, вычислим погрешности для управления и траекторий.
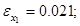
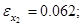
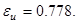
Пример 3. Пусть управляемый процесс описывается системой дифференциальных уравнений:
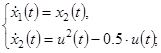 (15)
(15)
с начальными условиями:
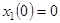 ,
,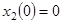 (16)
(16)
и следующими ограничениями на переменную времени:
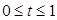 (17)
(17)
и на управление:
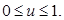 (18)
(18)
Критерий оптимизации имеет вид
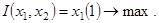 (19)
(19)
Требуется найти оптимальное программное управление 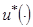 и соответствующую ему траекторию
и соответствующую ему траекторию 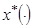 , которые удовлетворяют уравнениям (15)-(16), ограничениям (17)-(18) и условию (19).
, которые удовлетворяют уравнениям (15)-(16), ограничениям (17)-(18) и условию (19).
Аналитическое решение данной задачи представлено в [1].
На рис. 5 изображено численное решение данной задачи, при начальном приближении 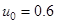 .
.
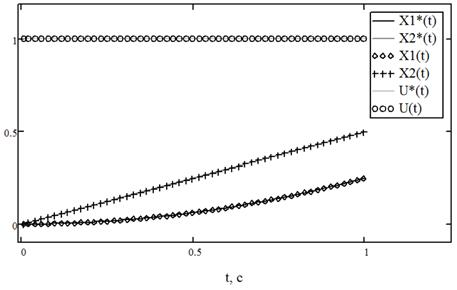
Рис. 5. Графики численного решения примера 3
Сравнивая полученные численные и аналитические значения, вычислим погрешности для управления и траекторий.
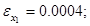
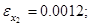
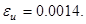
Выполненный сравнительный анализ приближенного и аналитического решения задач показал их удовлетворительное согласование между собой.
Литература:
1. Островский Г. М., Волин Ю. М. Методы оптимизации сложных химико-технологических схем. — М.: Химия. 1970. 328 с.
2. Понтрягин Л. С. Математическая теория оптимальных процессов. — М.: Наука. 1976. 392 с.
3. Мустафина C. А., Валиева Ю. А., Давлетшин Р. С., Балаев А. В., Спивак С. И. Оптимальные технологические решения для каталитических процессов и реакторов // Кинетика и катализ. 2005. Т. 46. № 5. С. 749–756.
4. Мустафина С. А., Балаев А. В., Смирнов Д. Ю., Спивак С. И. Моделирование каталитического процесса дегидрирования метилбутенов // Системы управления и информационные технологии. 2006. Т. 23. № 1. С. 10–14.
5. Федоренко Р. П. Приближенное решение задач оптимального управления. — М.: Наука. 1978. 488 с.







