Основная цель высшего образования заключается в повышении качества обучения студентов. Поэтому в процесс обучения во многих вузах вводится модульно-рейтинговая технология, предусматривающая дифференцированный подход к обучению студентов.
Модульно-рейтинговая система обучения позволяет отслеживать сформированность действий, адекватных программе изучаемого курса и уровень их усвоения, тем самым улучшается уровень подготовки студентов. Об этом свидетельствуют результаты проведенного нами педагогического эксперимента. Для его осуществления обучение в экспериментальной группе (ЭГ) было построено на основе модульно-рейтинговой технологии, и была проведена проверка их знаний после изучения темы «Обыкновенные дифференциальные уравнения». Результаты выполнения заданий приведены в таблице 1.
Таблица 1
|
Количество выполненных заданий |
Число студентов, справившихся с ними |
То же в % |
|
5 |
10 |
40 % |
|
4 |
11 |
44 % |
|
3 |
2 |
8 % |
|
2 |
1 |
4 % |
|
1 |
1 |
4 % |
|
ни одного |
- |
0 % |
|
Всего 25 студентов | ||
Анализируя таблицу, видим, что большинство студентов (21 из 25; 84 %) справились с заданиями успешно, выполнив 4–5 заданий из пяти. В литературе принято считать, что обучаемый обладает высоким уровнем овладения умением, если он правильно выполнил не менее 80 % заданий (в нашем случае 4–5 заданий), средним, если он выполнил правильно не менее 50 %, но меньше 80 % (в нашем случае 3 задания) и низким, если меньше 50 % (1–2 задания или ни одного). Это означает, что у 2 из 25 студентов (8 %) действия, адекватные учебному материалу, сформированы на репродуктивном уровне, у 2 из 25 (8 %) — на репродуктивно-преобразующем и у 21 из 25 (84 %) на преобразующем.
Заметим, что задания 1 и 2 контрольной работы были ориентированы на применение знаний в стандартной ситуации. Они соответствуют первому (репродуктивному) уровню усвоения учебного материала темы. Задания 3 и 4 направлены на применение знаний в видоизмененной ситуации и соответствуют второму (репродуктивно-преобразующему уровню) усвоения учебного материала. Пятое задание соответствует третьему (творческому) уровню усвоения учебного материала, так как необходимо применить знания в нестандартной ситуации.
По критерию правильности результаты отражены в таблице 2.
Таблица 2
|
Уровни |
Число студентов (всего 25 человек) |
То же в % |
|
Преобразующий |
21 |
84 % |
|
Репродуктивно-преобразующий |
2 |
8 % |
|
Репродуктивный |
2 |
8 % |
Для сравнения полученных результатов аналогичная контрольная работа была проведена контрольной группе (КГ), в которой обучение проводилось в традиционной форме. Результаты выполнения заданий в контрольной группе видны из таблицы 3.
Таблица 3
|
Количество выполненных заданий |
Число студентов, справившихся с ними |
То же в % |
|
5 |
2 |
8,7 % |
|
4 |
5 |
21,7 % |
|
3 |
10 |
43,5 % |
|
2 |
3 |
13 % |
|
1 |
2 |
8,7 % |
|
ни одного |
1 |
4,4 % |
|
Всего 23 студента | ||
Из таблицы 4 видно, что в контрольной группе выполнили верно 4–5 заданий всего 7 из 23 студентов (30,4 %). Это означает, что у 7 из 23 обучаемых (30,4 %) действия, адекватные учебному материалу, сформированы на преобразующем уровне, у 10 из 23 (43,5 %) — на репродуктивно-преобразующем уровне и у 6 из 23 (26,1 %) на репродуктивном уровне.
Таблица 4
|
Количество выполненных заданий |
Число студентов, справившихся с заданиями | |||
|
ЭГ (всего 25) |
КГ (всего 23) | |||
|
5 |
10 |
40 % |
2 |
8,7 % |
|
4 |
11 |
44 % |
5 |
21,7 % |
|
3 |
2 |
8 % |
10 |
43,5 % |
|
2 |
1 |
4 % |
3 |
13 % |
|
1 |
1 |
4 % |
2 |
8,7 % |
|
ни одного |
- |
0 % |
1 |
4,4 % |
Таблица 5
|
Уровни |
ЭГ (всего 25 студентов) |
КГ (всего 23 студента) | ||
|
Число студентов |
То же в % |
Число студентов |
То же в % | |
|
Преобразующий |
21 |
84 % |
7 |
30,4 % |
|
Репродуктивно-преобразующий |
2 |
8 % |
10 |
43,5 % |
|
Репродуктивный |
2 |
8 % |
6 |
26,1 % |
Таблица 6
|
Номер задания |
Число студентов, выполнивших задания | |||||||
|
ЭГ (всего 25) |
КГ (всего 23) | |||||||
|
верно |
в % |
неверно |
в % |
верно |
в % |
неверно |
в % | |
|
1 |
23 |
92 % |
2 |
8 % |
16 |
69,6 % |
7 |
30,4 % |
|
2 |
21 |
84 % |
4 |
16 % |
14 |
60,9 % |
9 |
39,1 % |
|
3 |
21 |
84 % |
4 |
16 % |
15 |
65,2 % |
8 |
34,8 % |
|
4 |
20 |
80 % |
5 |
20 % |
11 |
47,8 % |
12 |
52,2 % |
|
5 |
18 |
72 % |
7 |
28 % |
12 |
52,2 % |
11 |
47,8 % |
|
Всего |
103 |
82,4 % |
22 |
17,6 % |
68 |
59,1 % |
47 |
40,9 % |
Из таблицы 6 видно, что процент верных ответов в экспериментальной группе значительно выше, чем в контрольной. Проверим достоверность этого вывода средствами статистики, используя критерий согласия Т. В экспериментальной группе выполнено 103 задания из 125 (n2=125), что составляет 82,4 % (Р2=82,4 %). В контрольной группе всего выполнено 68 заданий из 115 (n1=115), что составляет 59,1 % (Р1=59,1 %).
Формула для Т имеет вид:
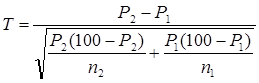 (1),
(1),
подставляя соответствующие значения, получаем:
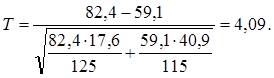
При значении Т ≥ 3 различия в результатах считаются существенными, обусловленными влиянием отдельного факта, в нашем случае таким фактом является методика обучения. Следовательно, более высокий процент правильно выполненных заданий студентами экспериментальной группы не случаен, а является результатом применения модульно-рейтинговой системы обучения.
Для большей объективности выводов проверим их достоверность, используя медианный критерий. В нашем случае n1= 25, n2= 23. Выборки X и Y являются упорядоченными множествами полученных баллов за выполнение заданий в ЭГ и КГ.
X: 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 2, 1;
Y: 5, 5, 4, 4, 4, 4, 4, 4, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 2, 2, 1, 1, 0.
Обе серии наблюдений объединяем в одну выборку, объем которой равен n1+n2 и обозначаем N. Для нахождения медианы измерения баллы записываем в ряд по возрастанию значений. Имеем N=48. Объединенная выборка в порядке возрастания равна:
0, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5.
Медиана численно равна среднему арифметическому значений балов, стоящих на 24 и 25 местах. Получаем: m=(4+4):2=4.
Гипотезы. Предположим, что законы распределения случайных величин X и Y одинаковы. Тогда выполняется и такое равенство: медиана значений хi равна медиане уj значений. Справедливость этого равенства проверяется с помощью медианного критерия. Таким образом, нулевая гипотеза Н0 имеет вид: обе совокупности, из которых взяты выборки, имеют одну и ту же медиану. В качестве альтернативной гипотезы выбирается гипотеза Н1: совокупности имеют разные медианы.
Если гипотеза Н1 справедлива, то отсюда следует, что законы распределения изучаемого свойства различны, т. е. состояние изучаемого свойства в рассматриваемых совокупностях существенно различно.
Таблица 7
|
|
ЭК (n1=25) |
КК (n2=23) |
|
Число оценок, больших m |
10 (A=11) |
2 (B=2) |
|
Число оценок, меньших или равных m |
15 (C=15) |
21 (D=21) |
Статистика критерия. Для проверки гипотез с помощью медианного критерия на основе наблюдений, записанных в таблице 7, подсчет ведется по формуле:
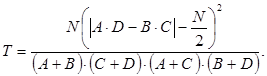
Подставляя значения в формулу статистики медианного критерия, получим:
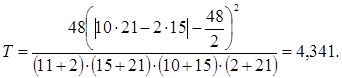
Правило принятия решения. Гипотеза Н0 отклоняется на данном уроне значимости α, если наблюдаемое значение Т>Хα, где Хα определяется по таблице для выбранного α. В нашем случае Т=4,341>3,841 при α=0,05. Следовательно, принимается альтернативная гипотеза Н1, с достоверностью 95 %, а значит, законы распределения изучаемого свойства различны, т. е. уровень усвоения учебного материала у студентов ЭГ и КГ существенно различны.
Таким образом, статистическая обработка данных по критерию согласия и медианному критерию показала, что в контрольной и экспериментальной группах различия в уровнях усвоения учебного материала является существенным, что обусловлено применением модульно-рейтинговой технологии обучения, направленной на управление учебной деятельностью студентов на занятиях математики.
Литература:
1. Вальчук Е. В., Ячинова С. Н. Тесты в модульно-рейтинговой системе обучения // Молодой ученый. — 2015. — № 8. — С.889–891.
2. Гудкова В. С., Ячинова С. Н. Пути повышения качества обучения математике студентов технических вузов // Молодой ученый. — 2015. — № 3 (83). — С. 755–758.
3. Гудкова В. С., Ячинова С. Н. Модульно-рейтинговая система как средство повышения качества обучения // Молодой ученый. — 2015. — № 8. — С. 910–912.
4. Крымская Ю. А., Ячинова С. Н. Пути повышения качества и мотивации обучения при профессиональной подготовке студентов в вузах // Молодой ученый. — 2014. — № 19. — С. 565–567.
5. Ячинова С. Н. Цели обучения как средство управления учебной деятельностью на уроке математики // Дис. канд. пед наук — Пенза, 2003. — 165с.

