Модифицированное уравнение Беллмана для эргодических марковских цепей с доходами

Управляемые марковские цепи с одним эргодическим классом и, возможно, с невозвратными состояниями изучаются с помощью операторов сжатия. Строится модифицированное уравнение Беллмана, позволяющее найти оптимальные стратегии не только на конечном, но и бесконечном горизонте. Представляется IB_m-метод динамического программирования, охватывающий как частный случай модифицированного уравнения Беллмана и итерационного алгоритма Ховарда. На его основе разрабатываются эффективные итерационные алгоритмы нахождения оптимальных стратегий на бесконечном горизонте.

 

Введение

Пусть задана управляемая марковская цепь с критерием средних доходов за единицу времени, удовлетворяющая условиям:

1)      любая стационарная стратегия задает марковскую цепь с одним эргодическим классом и, возможно, с невозвратными состояниями;

2)      каждый эргодический класс не имеет циклических подклассов.

Такую управляемую марковскую цепь назовем регулярной марковской моделью и обозначим RMM. Этот случай, по существу, является основным, заслуживающим внимания с точки зрения задач, встречающихся на практике.

В [1, 2] RMM рассматривается как частный случай общего марковского процесса принятия решений (структура цепи может меняться в зависимости от стратегии).

В настоящей работе, опираясь на одно замечательное свойство неотрицательно регулярной цепи Маркова (теорема 1), строятся операторы сжатия, неподвижные точки которых определяют оптимальное значение критерия качества стратегий RMM. С их помощью:

1)        строится модифицированное уравнение Беллмана, позволяющее найти оптимальные стратегии RMM не только на конечном, но и бесконечном горизонте управления,

2)        изучается вопрос существования стационарной оптимальной стратегии RMM,

3)        определятся оптимизационная схема последовательных приближений, которая порождает целый класс итерационных алгоритмов, позволяющих решать задачи оптимизации достаточно больших размерностей.

Аналогичная схема оптимизации использована в работах [3–6], применительно к управляемым марковским цепям с поглощением, марковским играм с переоценкой, рекурсивным играм, регулярным марковским играм.

Из результатов данной работы получается утвердительный ответ на вопрос, поставленный в книге [7, c. 25]: можно ли схему оптимизации, основанной на принципе сжатых отображений, эффективно распространить на модель динамического программирования со средним доходом за единицу времени.

1. Постановка задачи

Пусть имеется управляемая марковская цепь с конечным множеством состояний S = {1, 2, …, N} и конечными множествами решений U_i = {1, 2, …, k_i} (iÎS).

Элемент f = [u_i] (iÎS) из пространства F = U₁ × U₂ × … × U_N, где u_i ÎU_i, называется решающей функцией. Последовательность решающих функций p = (𝑓₁, 𝑓₂, …, 𝑓_n, …) называется марковской стратегией, где 𝑓_n — решающая функция, применяемая на n-м шаге, а u_i(n) (i-й элемент вектора 𝑓_n) является решением, принимаемым в состоянии i. Стратегия вида 𝑓^¥ = (𝑓, 𝑓, …, 𝑓, …) называется стационарной. Для каждой решающей функции 𝑓ÎF заданы матрица вероятностей переходов 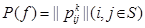 размера (N×N) и (N×1)-мерный вектор доходов 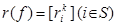, где k = u_iÎU_i. Обозначим: P — множество марковских стратегий, F ^¥ — множество стационарных стратегий.

Для управляемых марковских цепей с конечным горизонтом n цель управления состоит в максимизации (N×1)-мерного вектора суммарных средних доходов за n шагов

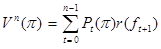                                                                                                (1)

в множестве стратегий P = {π}, где P_t(p) = P(f₁)P(f₂)…P(f_t), P₀(p) = I (I — единичная матрица размера N×N); i-й элемент 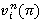 вектора  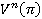отвечает начальному состоянию процесса iÎS.

В случае, когда горизонт управления бесконечен, в качестве критерия оптимальности выбирается вектор средних доходов за единицу времени

𝛤(π) = 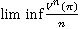 при n →∞.                                                                                   (2)

Здесь начальному состоянию iÎS отвечает i-й элемент 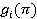 вектора 𝛤(p).

Стратегия π^*ÎP оптимальна, если 𝛤(π^*) ≥ 𝛤(π) для всех πÎP.           

Наша цель — решить задачу оптимального управления регулярных марковских моделей с вектором средних доходов за единицу времени Г(π) с помощью принципа сжатых отображений и функционального уравнения Беллмана, и разработать эффективные методы нахождения оптимальных решений (π^*, 𝛤(π^*)) таких моделей.

3. Вспомогательные результаты

Обозначим 𝕍^N множество N-мерных вектор столбцов. Вектор из 𝕍^N, все элементы которого равны единице, обозначим 1 (векторная единица).

При фиксированной стационарной стратегии 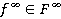 RMM характеризуется положительной или неотрицательной регулярной цепью Маркова с матрицей вероятностей перехода 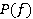. Согласно теории цепей Маркова [8] в этом случае существует предельная матрица 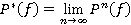, состоящая из одинаковых строк α(𝑓) = [α_i(𝑓)](iÎS)Î𝕍^N. Иначе говоря, P^*(𝑓) = 1α(𝑓). Вектор α(𝑓) есть финальное распределение вероятностей, удовлетворяющий уравнению α(𝑓) = α(𝑓)P(𝑓) при условии α(𝑓)1 = 1. Отсюда и из (2) следует, что

𝛤(𝑓) = P^*(𝑓)r(𝑓) = 1α(𝑓)r(𝑓) = 𝑔(𝑓)1,                                                                     (3)

где 𝑔(𝑓) — скалярная величина (называется прибыль).

Таким образом, для RMM в множестве стационарных стратегий F^∞ предельный средний доход не зависит от начального состояния iÎS, т. е. 𝑔_i (𝑓) = 𝑔(𝑓) для всех iÎS.

Лемма 1. Для RMM справедливо равенство Vⁿ(𝑓^¥) = n𝑔(𝑓)1 + 𝑣(𝑓) + ε_n(𝑓), n ≥ 1, где ε_n(𝑓) → 0 при n → ∞ и 𝑣(𝑓) =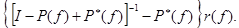

Д о к а з а т е л ь с т в о (см. [2], c. 42).

Элементы 𝑣_i(𝑓), iÎS вектора 𝑣(𝑓) называются весами, а величины 𝑣_i(𝑓) — 𝑣_s(𝑓), iÎS \{s}, где s произвольный элемент S — относительными весами.

В [1, 2] RMM рассматривается как частный случай общего марковского процесса принятия решений (при фиксированной стратегии 𝑓^¥ множество состояний разбивается на несколько эргодических множеств и невозвратное множество, которые могут меняться в зависимости от стратегии 𝑓^¥). В этом случае итерационный алгоритм Ховарда приобретает такой вид (см. [2, c. 82]):

1.      Для выбранной решающей функции f = [u_i] (iÎS) Î F решить систему уравнений

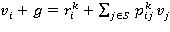, iÎS                                                                                     (4)

относительно весов 𝑣_i = 𝑣_i(𝑓), iÎS и прибыли 𝑔 = 𝑔(𝑓) полагая 𝑣_s = 0 для некоторого эргодического состояния sÎS, где k = u_i.

2.      Используя найденные значения 𝑔 и 𝑣_i, iÎS, найти при каждом iÎS решение

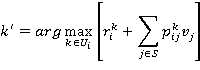
и принять его за новое решение в состоянии i. Здесь следует соблюдать правило выбора решения: если старое решение в i-м состоянии приносит величине критерия столь же большое значение, как и любое другое решение, необходимо оставить старое решение неизменным. Процедура заканчивается, когда в двух последовательных итерациях будут получены одинаковые решающие функции, в противном случае можно перейти к пункту 1.

Решающую роль в изучении RMM играет следующая

Теорема 1 [6, 9]. Пусть марковская цепь, задаваемая матрицей 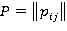 (1 ≤ i, j ≤ N), положительно или неотрицательно регулярна. Пусть Q_s — матрица размера (N–1)×(N–1), полученная из матрицы P вычитанием произвольной s-ой строки из оставшихся N–1 строк и вычеркиванием s-ой строки s-го столбца. Тогда спектральный радиус ρ(Q_s) матрицы Q_s меньше единицы.

4. RMM в стационарном режиме

Приведем некоторые свойства RMM в множестве стационарных стратегий F^¥. Поскольку в данном разделе рассматривается конкретная стационарная стратегия 𝑓^¥ÎF^¥, для краткости, соответствующие ей вектор доходов r(𝑓) и матрицу вероятностей переходов P(𝑓) будем обозначать через r и P соответственно, а их элементов 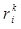 и 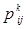 писать без верхнего индекса k.

Пусть величина 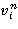 представляет собой суммарный средний доход, полученный к моменту n при стационарной стратегии 𝑓^¥ÎF^¥. Тогда в силу (1) имеет место рекуррентное соотношение

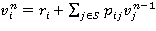 , iÎS.                                                                                      (5)

Лемма 2. Для RMM при любом sÎS справедливо равенство

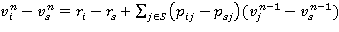                                                  (6)

для всех iÎS_s и n ≥ 1 при произвольном 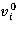, jÎS_s, где S_s = S \ {s}.

Положим

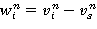, iÎS_s, 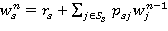.                                                         (7)

Теперь равенство (6) может быть записано в виде

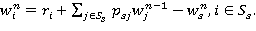                                                                       (8)

Величины 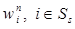 называются относительными оценками.

Введем величину σ_ij (i, jÎS) такую, что σ_ij = 1, если i ¹ j и σ_ii = 0. Заметим, что σ_ij = 1 — δ_ij, где δ_ij — символ Кронекера.

Лемма 3. Для RMM при любом sÎS существуют конечные пределы 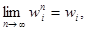 iÎS_s. При этом имеет место равенство w_s = 𝑔(𝑓) и разложение

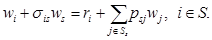                                                                                  (9)

Предложение 1. Для RMM величины 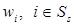 представляют собой относитель-ные весы.

Предложение 2. Для RMM система уравнений (9) имеет единственное решение, такое, что

w_s = 𝑔(𝑓), w_i = 𝑣_i(𝑓) — v_s(𝑓), iÎS_s.                                                                           (10)

Предложение 3. Для RMM, прежде чем решать соответствующую систему уравнений Ховарда (4), можно приравнивать к нулю любое из весов v_i, iÎS.

Таким образом, в случае неотрицательной регулярной цепи, вопреки утверждению в [2], нет необходимости отыскивать (при большом N это достаточно сложно) некоторое существенное состояние s, чтобы положить v_s = 0. Здесь, так же как в положительно регулярной цепи, можно положить v_N = 0.

5. Построение операторов сжатия для RMM

Перейдем теперь к изучению RMM с помощью операторов сжатия.

Рассмотрим оператор L(𝑓), отображающий пространство 𝕍^N–1 в себя, определяемый равенством

L(f) (w)_s = [L_i(u_i) (w)_s — L_s(u_s) (w)_s] (iÎS_s),

где (w)_s = [w₁, …, w_s–1, w_s+1, …, w_N]^T Î 𝕍^{N –1},

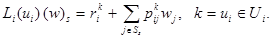
Теорема 2. Для RMM при любой 𝑓ÎF оператор L(𝑓) является на 𝕍^{N –1} сжатием. При этом L(𝑓) имеет в 𝕍^N–1 единственную неподвижную точку (w(𝑓))_s и последова-тельные приближения

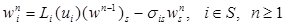                                                                (11)

сходится к (w(𝑓))_s = [𝑣_i(𝑓) — 𝑣_s(𝑓)] (iÎS_s), начиная с любого (w⁰)_sÎ𝕍^N–1, причем 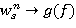 при n → ∞.

Данная теорема показывает, что задача нахождения предельного среднего дохода g и относительных весов w_i, iÎS_s может быть сведена к эффективной рекуррентной процедуре последовательных приближений (7)−(8) с геометрической скоростью сходимости. Рекуррентные соотношения (7)−(8) по существу представляют собой метод простой итерации [10] и могут найти приложения даже в случае, когда число состояний N велико и применение метода Гаусса для решения системы уравнений Ховарда (4) невозможно.

Следует заметить ещё одно достоинство рекуррентной процедуры (7)−(8), состоящее в том, что при ее реализации можно прекратить вычисление на любом шаге итерации и использовать приближенные значения wⁿ для улучшения решения и принять wⁿ в качестве начального приближения для нового решения. Далее будет обсужден вопрос о возможности такого подхода в нахождении стационарной оптимальной стратегии RMM.

Рассмотрим теперь оператор Λ, отображающий пространство 𝕍^N–1 в себя, определяемый равенством

Λ(w)_s = [Λ_i (w)_s] (iÎS_s), (w)_s Î 𝕍^{N –1},                                                                            (12)

где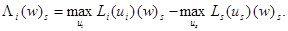

Поскольку 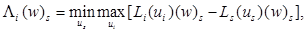 оператор Λ может быть пред-ставлен в виде 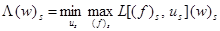, (w)_sÎ𝕍^{N –1}, где (𝑓)_s = (u₁, …, u_s–1, u_s+1, …, u_N). Ясно, что 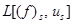есть L(𝑓).

Теорема 3. Для RMM оператор Λ является на 𝕍^N–1 сжатием. При этом Λ имеет в 𝕍^N–1 единственную неподвижную точку (w)_s и последовательные приближения

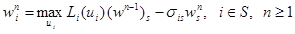                                                             (13)

сходится к (w)_s, начиная с любого (w⁰)_s Î 𝕍^N–1.

6. Модифицированное уравнение Беллмана

Рассмотрим RMM с конечным горизонтом n. Критерий оптимальности в этом случае характеризуется величиной 𝑉ⁿ(π) — (N×1)-мерным вектором суммарных средних доходов (1). Здесь стратегия π определяется как последовательность (…, f_n, f_n–1, …, f₁) элементов множества F, где f_n — решающая функция, применяемая за n шагов до окончания процесса принятия решений. Множество таких «восточных» стратегий обозначим 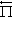. При восточной стратегии π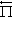Πдля вектора суммарных доходов имеет место рекуррентное соотношение

𝑉ⁿ(π) = r(𝑓_n) + P(𝑓_n)𝑉^n–1(π), n ≥ 1,

где 𝑉⁰(π) = 0 (нулевой вектор столбец).

Определение 1. Стратегия π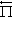^*Πравномерно оптимальна, если для любой стратегии π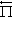Πи любого n ≥ 1 выполняется неравенство 𝑉ⁿ(π^*) ≥ 𝑉ⁿ(π).         

Заметим, что если стратегия π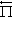^*Πравномерно оптимальна, то она также оптимальна, но обратное утверждение неверно.

Равномерно оптимальная стратегия π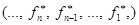^* =  произвольной управ-ляемой марковской цепи с конечным числом шагов определяется с помощью метода динамического программирования — функционального уравнения Беллмана [2]:

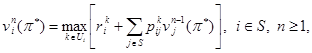                                                         (14)

при начальном условии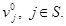

Определение 2. Стратегия π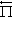Πквазистационарна, если, начиная с некоторого n′ < ∞, имеет место равенство f_n = f для всех n ≥ n′.

Напишем рекуррентное соотношение (13) в развернутом виде

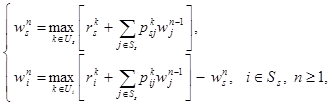                                                   (15)

где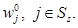

Рекуррентные соотношения (15) назовем модифицированным уравнением Беллмана.

Поскольку для RMM в (15) wⁿ → w при n → ∞, то справедливо

Следствие 1. Для RMM стратегия πÎ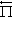, порожденная модифицированным уравнением Беллмана (15) с соблюдением правила выбора решения, квазистационарна.

Теорема 4. Пусть для RMM в функциональном уравнении Беллмана (14)начатом 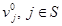 и в модифицированном уравнении Беллмана (15) начатом  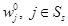соблюдено правило выбора решения. Тогда, решающие функции {𝑓_n} и 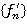, порожденные рекуррентными соотношениями (14) и (15) соответственно, являются идентичными, т. е.

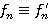 для всех n = 1, 2, …. (16)

Следствие 2. Для RMM стратегия πÎ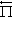, порожденная модифицированным уравнением Беллмана (15), равномерно оптимальна.

Следствие 3. Для RMM стратегия π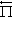Πпорожденная функциональным уравнением Беллмана (14) с соблюдением правила выбора решения, квазистационарна.

Например, в задаче водителя такси [1, 2] решающая функция 𝑓₃ = [2, 2, 2]^T, полученная методом динамического программирования, начинает повторяться уже с третьего шага итерации; 𝑓₃ = 𝑓₄ = 𝑓₅ = ….

Теорема 5. Для RMM стратегия π^*Î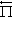, порожденная модифицированным уравнением Беллмана (15)начатом  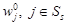доставит критерию оптимальности 𝛤(π) максимальное значение, причем все компоненты  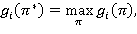i∊S вектора 𝛤(π^*) равны между собой.

Следствие 4. Для RMM существует стационарная оптимальная стратегия, максимизирующая средний доход за единицу времени.

Следствие 5. Для RMM последовательность решающих функций {𝑓_n, n = 1, 2, …}, порожденная модифицированным уравнением Беллмана (15) с соблюдением правила выбора решения при любом начальном приближении 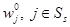 сходится к пределу 𝑓^*ÎF такому, что 𝑓^*∞ — оптимальная стратегия, причем  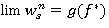и 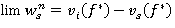, iÎS_s при n → ∞.

Следствие 6. Для RMM система функциональных уравнений

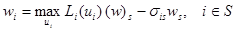
имеет единственное решение (w)_s = (w(f ^*))_s такое, что w_i = 𝑣_i(𝑓^*) — 𝑣_s(𝑓^*), jÎS_s, причем w_s = 𝑔(𝑓^*), а 𝑓^*∞ — стационарная оптимальная стратегия.

Таким образом, модифицированное уравнение Беллмана (15) позволяет решать задачу оптимизации RMM как на конечном, так и бесконечном горизонтах. При этом, в случае бесконечного управления, итерационный алгоритм (15) выгодно отличается от итерационного алгоритма Ховарда отсутствием необходимости решения систем линейных алгебраических уравнений в каждой итерации, а в случае конечного управления, выгодно отличается от функционального уравнения Беллмана (14) отсутствием проблемы переполнения памяти ЭВМ за счет значения суммарных средних доходов 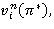i∊S, которые при чрезмерно большом n могут превышать возможности запоминающего устройства ЭВМ.

7. IB_m-метод динамического программирования

Положив L¹(f) ≡ L(f), Λ¹ ≡ Λ введем на 𝕍^N–1 операторы вида

L^m(f)(w)_s = L(f)L^m–1(f)(w)_s, m = 2, 3, …, (w)_s Î 𝕍^N–1;                                                    (17)

Λ^m(w)_s = L^m(f ^*)(w)_s, m = 2, 3, …, (w)_s Î 𝕍^N–1,                                                             (18)

где элементы 𝑓^* определяются равенством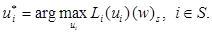

Теорема 6. Для RMM оператор Λ^m при любом m ≥ 1 на 𝕍^N–1 является сжатием. При этом Λ^m при любом m ≥ 1 имеет в 𝕍^N–1 единственную неподвижную точку (w)_s = (w(f ^*))_s такую, что w_i = 𝑣_i(𝑓^*) — 𝑣_s(𝑓^*), iÎS_s, причем w_s = 𝑔(𝑓^*), а 𝑓^*∞ — оптимальная стратегия.

В соответствии с (17) и (18) и принципа сжимающих отображений для заданного m ≥ 1 образуем, так называемое, m-уравнение преобразование относительных оценок

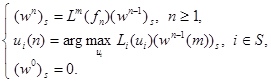
Эти соотношения могут быть записаны в развернутом виде

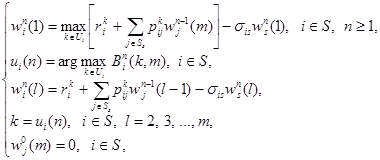                                        (19)

где  означает выражения, стоящего в квадратных скобках.

Метод последовательных приближений, определенный рекуррентными соотношениями (19) назовем IB_m-методом динамического программирования. Заметим, что IB₁-метод представляет собой модифицированное уравнение Беллмана (15), а IB_∞-метод — итерационный алгоритм Ховарда, изложенного в разделе 3.

Введем отношение ⋝ на множестве 𝕍^N следующим образом: a ⋝ b, если a_i ≥ b_i для всех 1 ≤ i ≤ N и a ¹ b (a, bÎ 𝕍^N).

Лемма 4. Для RMM если при некотором 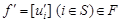 выполнено неравенство

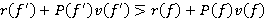,                                                                    (20)

то 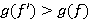, где 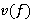 — вектор весов.

Следствие 7. Для RMM если при некотором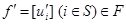 выполнены неравен-ства

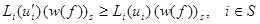                                                                      (21)

и хотя бы для одного iÎS неравенства (21) строго больше, то 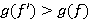 где (w(𝑓))_s = (𝑣(𝑓) — 𝑣_s(𝑓)1)_s — вектор относительных весов.

Теорема 7. Для RMM при любом конечном или бесконечном m последовательность решающих функций {f_n, n = 1, 2, …}, порожденная IB_m-методом (19) с соблюдением правила выбора решения при любых 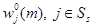 сходится к пределу 𝑓^*ÎF такому, что 𝑓^*¥ — оптимальная стратегия, причем  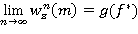и 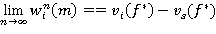, iÎS_s.

Следствие 8. Для RMM для любого конечного или бесконечного m существует конечное число k_m ≥ 1 такое, что стратегия 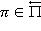, порожденная IB_m-методом (19) с соблюдением правила выбора решения, квазистационарна такая, что 𝑓_n = 𝑓^* для всех n ≥ k_m, где 𝑓^*¥ — оптимальная стратегия.

Теорема 8. Для RMM найдется конечное число m_IB ≥ 1 такое, что стратегия 𝑓^*¥, полученная из соотношения IB_m-метода (19)

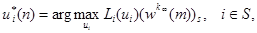
будет оптимальна при любых m ≥ m_IB.

Следствие 9. Для RMM скорость сходимости IB_m-метода (19) возрастает с возрастанием m и максимальна при m ≥ m_IB.

Полученные результаты определяют оптимизационную схему последовательных приближений, которая порождает целый класс итерационных алгоритмов, зависящих от параметра m.

Итерационный алгоритм 1:

1.      Задать ε > 0, sÎS и m ≥ 1. Выбрать произвольное (w⁰(m))_s Î 𝕍^N–1.

2.      C помощью (19), соблюдая правило выбора решения, вычислить wⁿ(m) до тех пор, пока не будет выполнено условие 𝑓_n = 𝑓_n–1.

3.      Если || (wⁿ(m))_s — (w^n–1(m))_s || ≤ ε, то 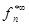— оптимальная стратегия, а величина  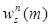— равна среднему доходу за единицу времени с точностью ε. В противном случае

4.      Положив (w⁰)_s = (wⁿ(m))_s с помощью рекуррентного соотношения (11) вычислить вектор относительных весов (w(f_n))_s с точностью ε. Затем, положив (wⁿ(m))_s = (w(f_n))_s перейти к пункту 2.

При значении параметра m = m_IB итерационный алгоритм 1 достигает свою наибольшую эффективность. В этом случае первая появившаяся субоптимальная решающая функция (решающая функция, остававшаяся неизменной на следующем шаге) будет оптимальной. Однако число m_IB заранее неизвестно. В идеальном случае m_IB = 1, при котором объем вычислений будет наименьшим. В связи с этим вычисления целесообразно начинать со значения m = 1. Если при этом, субоптимальная стратегия окажется неоптимальной, то на следующем шаге итерации m увеличивается на одну единицу. Эти соображения приводят к следующему варианту оптимизационной процедуры с переменным параметром m.

Итерационный алгоритм 2:

Этот алгоритм отличается от итерационного алгоритма 1 тем, что в пункте 1 полагается m = 1, а в пункте 4 — m = m + 1.

Заключение

Отправной точкой анализа RMM послужило утверждение теоремы 1. Опираясь на него, построен оператор сжатия (13), определяющий алгоритм итерации решающих функций — модифицированное уравнение Беллмана (15), которое при конечном горизонте порождает оптимальную марковскую стратегию, а при бесконечном горизонте сходится к решению RMM в стационарном режиме. Модифицированное уравнение Беллмана (15) позволило установить существование стационарной оптимальной стратегии (следствие 4) и выявить одно замечательное свойство функционального уравнения Беллмана (14) (следствие 3).

Для RMM построен IB_m-метод динамического программирования (19), который при m = 1 представляет собой модифицированное уравнение Беллмана, а при m = ∞ — итерационный алгоритм Ховарда для управляемой марковской цепи с одним эргодическим классом и, возможно, с невозвратными состояниями. Тем самым он является одновременно их обобщением и развитием. Следует отметить, что IB_m-метод динамического программирования при любом m (1 ≤ m < ∞) выгодно отличается от итерационного алгоритма Ховарда отсутствием необходимости решения системы линейных алгебраических уравнений в каждой итерации. Такое положение позволяет решать задачи оптимизации управляемых марковских цепей достаточно больших размерностей при критерии средних доходов за единицу времени.

Вопрос о применимости метода Зейделя для ускорения сходимости модифицированного уравнения Беллмана остается открытым.

ПРИЛОЖЕНИЕ

Леммы 2–3, предложение 2, теоремы 2–4, теорема 5 и ее следствия 4–6 представлены и доказаны в рамках регулярных марковских игр (см. [6]). Заметим, что когда один из двух игроков пассивен (не имеет возможности выбора стратегии), регулярная марковская игра представляет собой RMM.

Доказательство теоремы 6. Как показано в [6] для матрицы Q_s(𝑓) из теоремы 1 существует матричная норма 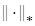 такая, что 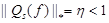. Число η является коэффициентом сжатия оператора L(𝑓), что следует из соотношения L(𝑓)(w)_s = d(𝑓) + Q_s(𝑓)(w)_s, где d(𝑓) = 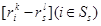Î𝕍^N–1, k = u_iÎU_i, l = u_sÎU_s. Сжимаемость оператора L^m(𝑓) вытекает из равенства  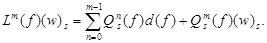Именно, для произвольных (w′)_s и (w′′)_s из 𝕍^N–1

|| L^m(f)(w′)_s — L^m(f)(w′′)_s || = 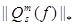|| (w′)_s — (w′′)_s || = η^m|| (w′)_s — (w′′)_s ||

и, следовательно, L^m(𝑓) есть оператор сжатия. Рассуждения, аналогичные использованными при доказательстве теоремы 3 (см. [6], теорема 3), приводят к тому, что || Λ^m(w′)_s — Λ^m(w′′)_s || ≤ ρ^m||(w′)_s — (w′′)_s ||, 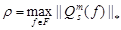, т. е. оператор Λ^m есть сжатия.

Пусть (w)_s — единственная неподвижная точка оператора Λ^m. Тогда справедливы равенства (w)_s = Λ^m(w)_s = L^m(𝑓^*)(w)_s = L(𝑓^*)(w)_s, где элементы 𝑓^* определяются равенством 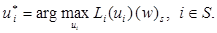 С другой стороны

Λ^mL(𝑓^*)(w)_s = L(𝑓^*)Λ^m(w)_s = L(𝑓^*)(w)_s.

Это значит, что L(𝑓^*)(w)_s также является неподвижной точкой оператора Λ^m. Но Λ^m имеет на 𝕍^N–1 единственную неподвижную точку и, следовательно, L(𝑓^*)(w)_s = (w)_s. Отсюда и из теоремы 2 и следствия 6 следует утверждение теоремы. Теорема 6 доказана.

Доказательство леммы 4. Пусть γ — (N×1)-мерный вектор такой, что γ = r(𝑓′) + + P(𝑓′)𝑣(𝑓) − r(𝑓) − P(𝑓)𝑣(𝑓) ⋝ 0. Для двух решающих функций 𝑓′ и 𝑓 из F согласно (4) имеем

𝑔(𝑓′)1 + 𝑣(𝑓′) = r(𝑓′) + P(𝑓′)𝑣(𝑓′),                                                                          (П.1)

𝑔(𝑓)1 + 𝑣(𝑓) = r(𝑓) + P(𝑓)𝑣(𝑓).                                                                               (П.2)

Вычитая (П.2) из (П.1) и полагая Δ𝑔 = 𝑔(𝑓′) — 𝑔(𝑓), Δ𝑣 = 𝑣(𝑓′) — 𝑣(𝑓), получим Δ𝑔1 + Δ𝑣 = γ + P(𝑓′)Δ𝑣. Умножая обе части этого равенства слева на предельный вектор α(𝑓′), получим Δ𝑔 = α(𝑓′)Δ𝑔1 = α(𝑓′)γ ≥ 0, поскольку α_j(𝑓′) ≥ 0 при всех jÎS в силу предположения неотрицательно регулярности цепи Маркова. Далее достаточно доказать, что Δ𝑔¹ 0. Предположим противное, т. е., что Δ𝑔 = 0. Тогда 𝑔(𝑓′) = 𝑔(𝑓) и условие (21) эквивалентно неравенстве r(𝑓′) + P(𝑓′)𝑣(𝑓) ⋝ 𝑔(𝑓′)1 + 𝑣(𝑓). Умножая обе части этого неравенства слева на предельную матрицу P^*(𝑓′), получим P(𝑓′)𝑣(𝑓) ⋝ P(𝑓′)𝑣(𝑓). Это противоречие доказывает лемму.

Доказательство теоремы 7. Согласно теореме 6 последовательность {(wⁿ(m))_s, n ≥ 1} при любом конечном m сходится к (w)_s — единственной неподвижной точке оператора Λ^m. Значит, если будет соблюдено правило выбора решения, стратегия π = 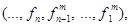где f ^m = (f, f, …, f) — последовательность, состоящая из m однотипных элементов вида f, порожденная IB_m-методом является квазистационарной, т. е. найдется конечное число k_m такое, что 𝑓_n = 𝑓^* для всех n ≥ k_m, где 𝑓^*¥ — оптимальная стратегия.

В случае m = ∞ на каждом шаге итерации n имеем решающую функцию 𝑓_n, которая является либо искомой (случай, когда 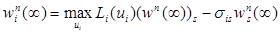 для всех iÎS), либо имеет стационарное улучшение 𝑓_n+1 (случай, когда  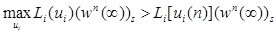хотя бы для одного iÎS); тогда согласно следствию 7 𝑔(𝑓_n+1) > 𝑔(𝑓_n). Поскольку существует лишь конечное число стационарных стратегий, то за конечное число итераций k_∞ найдется решающая функция 𝑓_n = 𝑓^*, которая не имеет стационарных улучшений. Следовательно, она должно быть искомой, образующая оптимальную стационарную стратегию 𝑓^*¥. Теорема доказана.

Доказательство теоремы 8. Поскольку для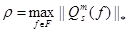

|| (w(f ^*))_s — (wⁿ(m))_s || = || Λ^m(w(f ^*))_s — Λ^m(w^{n — 1}(m))_s || ≤

≤ ρ^m|| (w(f ^*))_s — (w^{n — 1}(m))_s ||, где (w(f ^*))_s = (𝑣(𝑓^*) — 𝑣_s(𝑓^*)1)_s,

скорость сходимости IB_m-метода возрастает с возрастанием m. Следовательно, для целых чисел k_m, m ≥ 1 определенных выше, имеет место неравенство k_m ≥ k_m+1. С другой стороны, монотонно убывающая последовательность {k_m, m ≥ 1} ограничена снизу числом k_∞. Это значит, что найдется число m_IB < ∞ такое, что k_m = k^* для всех m ≥ m_IB. Ниже устанавливается, что k^* = k_∞.

Пусть 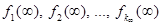 — решающие функции, найденные IB_∞-методом (итерационным алгоритмом Ховарда начатым со второго шага, изложенным в разделе 3). Покажем, что эти же решающие функции могут быть определены IB_m-методом, если положить m ≥ m_IB.

Из (19) следует, что при любом m ≥ 1 IB_m-метод вначале итерационного процесса определяет решающую функцию f₁(m) = f₁(∞). Далее с помощью третьего рекуррентного соотношения (19) вычисляются величины 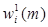, iÎS, которые согласно теореме 2 при m → ∞ стремятся к величинам 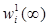, iÎS таким, что  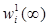= w_i(𝑓₁(∞)) = 𝑣_i(𝑓₁(∞)) — 𝑣_s(𝑓₁(∞)), iÎS_s, 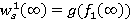. Отсюда видно, что величины 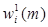, iÎS представляют собой решение системы уравнений Ховарда (4) для 𝑓₁(∞)ÎF. Следующей решающей функцией, определяемая IB_m-методом будет 𝑓₂(m)ÎF. Из сходимости 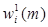→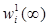, iÎS следует сходимость 𝑓₂(m) → 𝑓₂(∞), при m → ∞. Это значит, что найдется такое конечное число m₂, что 𝑓₂(m₂) = 𝑓₂(∞). Следовательно, если в IB_m-методе положить m = m₂, то после двух итераций получаются решающие функции 𝑓₁(∞) и 𝑓₂(∞).

Аналогичным образом можно установить существования конечных чисел m₃, m₄, …, 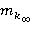 таких, что 𝑓_k(m_k) = 𝑓_k(∞), k = 3, 4, …, k_∞. Теперь, если положить m = max{m₃, m₄, …, 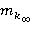} (m₁ = 1), то IB_m-метод за k_∞ итераций порождает решающих функций 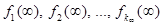. Отсюда можем заключить, что k^* = k_∞. Теорема 8 доказана.

 

Литература:

 

1.      Ховард Р. Динамическое программирование и марковские процессы. М.: Сов. Радио, 1964. 192 c.

2.      Майн Х., Осаки С. Марковские процессы принятия решений. М.: Наука, 1977. 176 c.

3.      Ибрагимов А. А. Об управляемых марковских процессах с поглощением // РАН. Автоматика и телемеханика. 1999. № 12. С. 80–89.

4.      Ибрагимов А. А. О существовании и единственности ситуации равновесия в марковских играх с переоценкой // НАН Украины. Кибернетика и системный анализ. 2000. № 6. С. 152–165.

5.      Ибрагимов А. А. Существование и нахождение значения и оптимальных стратегий в рекурсивных играх // Известия РАН. Теория и системы управления. 2001. № 4. С.102–109.

6.      Ибрагимов А. А. Существование и нахождение значения и оптимальных стратегий в регулярных марковских играх // Известия РАН. Теория системы управления. 2002. № 3. С. 29–40.

7.      Бертсекас Д., Шрив С. Стохастическое оптимальное управление: случай дискретного времени. M.: Наука, 1985. 208 c.

8.      Саримсаков Т. А. Основы теории процессов Маркова. Ташкент: Фан, 1988. 248 c.

9.      Ибрагимов А. А. Об одном свойстве регулярной цепи Маркова // Украинский математический журнал. 2002. Т 54. № 4. С. 466–471.

10.  Крылов В. И., Бобков В. В., Монастырный П. И. Вычислительные методы. Т. 1. М.: Наука, 1976. 304 с.