Основные виды кинетических процессов (набор прочности; изменение модуля упругости; контракция и усадка; нарастание внутренних напряжений; тепловыделение; изменение водопоглощения, водостойкости и химической стойкости и др.) формально описываются идентичными кинетическими уравнениями, а именно, решениями задачи Коши для обыкновенного дифференциального уравнения второго порядка [1…3]. Правда, как показывает практика, рассмотренные кинетические модели не всегда можно использовать для описания процессов в полидисперсных композиционных материалах. При их описании можно воспользоваться методами ретроспективной идентификации процессов по данным нормального функционирования (по синхронным измерениям фазовых координат в процессе нормальной эксплуатации).
Кинетические процессы второго порядка (увеличение порядка, не меняя сути, лишь усложняет техническую реализацию) можно описать уравнением вида:
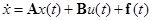 ,
, 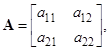
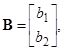
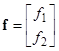 . (1)
. (1)
Если хотя бы одно из чисел 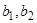 не равно нулю, то матрицу B можно записать виде
не равно нулю, то матрицу B можно записать виде 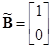 . Действительно, при
. Действительно, при 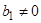 ,
, 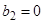 обозначим
обозначим 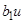 снова через u;если
снова через u;если 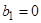 ,
, 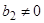 , то обозначим
, то обозначим 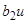 через u, перенумеруем уравнения и координаты
через u, перенумеруем уравнения и координаты 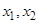 системы. Каноническим видом матрицы В будет вектор-столбец
системы. Каноническим видом матрицы В будет вектор-столбец 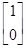 . Изменив масштаб, коэффициент усиления всегда можно привести к 1. Если ни одно из чисел
. Изменив масштаб, коэффициент усиления всегда можно привести к 1. Если ни одно из чисел 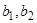 не является нулем, то каноническое по управлению представление можно получить, используя невырожденное линейное преобразование с матрицей С:
не является нулем, то каноническое по управлению представление можно получить, используя невырожденное линейное преобразование с матрицей С:
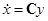 ,
, 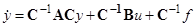 (2)
(2)
(из не вырожденности матрицы С следует наблюдаемость системы).
Вид матрицы 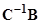 зависит от выбора матрицы С. В частности:
зависит от выбора матрицы С. В частности: 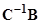 =
=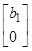 , если
, если
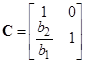 . Произведя масштабирование u, получим канонический вид
. Произведя масштабирование u, получим канонический вид 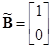 . При выборе матрицы С возможен некоторый произвол (два свободных параметра). В общем случае каноническое по управлению представление системы (1) будет иметь вид
. При выборе матрицы С возможен некоторый произвол (два свободных параметра). В общем случае каноническое по управлению представление системы (1) будет иметь вид
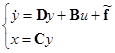 ,
,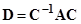 ,
, 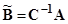 ,
, 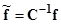 (3)
(3)
Собственные числа матриц А и D одинаковы (следует из общей теории линейных операторов: матрицы А и D — подобны). Здесь
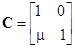 ,
,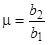 ;
;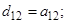
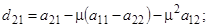
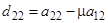 . (4)
. (4)
Возможны три принципиально различных случая.
1. 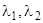 - вещественные собственные числа матрицы А и им соответствуют два линейно независимых вектора (в случае
- вещественные собственные числа матрицы А и им соответствуют два линейно независимых вектора (в случае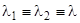 имеем
имеем 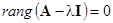 ).
).
Пусть 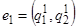 ,
, 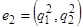 — собственные векторы;
— собственные векторы; 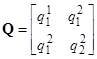 .
.
Заменой 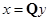 система (1) приведется к виду
система (1) приведется к виду
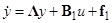 ,
,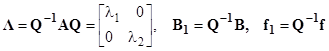 . (5)
. (5)
Возможны случаи:
1) 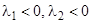 ; 2)
; 2) 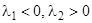 ; 3)
; 3) 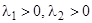 ;
;
4) 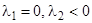 ; 5)
; 5) 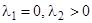 ; 6)
; 6) 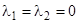
(учтена возможность перенумерации 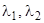 ).
).
2. Если 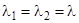 и
и 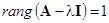 преобразование Q определится через собственный вектор
преобразование Q определится через собственный вектор 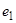 и присоединенный
и присоединенный 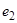 :
: 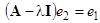 . При этом матрица (основная) системы преобразуется к виду
. При этом матрица (основная) системы преобразуется к виду 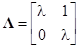 .
.
Качественно различных систем здесь три: 7) 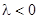 ; 8)
; 8) 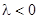 ; 9)
; 9) 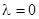 ; 6) и 9) отличаются структурой матрицы
; 6) и 9) отличаются структурой матрицы 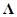 .
.
3. 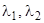 - комплексно сопряженные. Систему (1) можно записать в виде (5), но уже в комплексифицированном пространстве.
- комплексно сопряженные. Систему (1) можно записать в виде (5), но уже в комплексифицированном пространстве.
Качественно различных систем здесь три: 10) 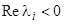 ; 11)
; 11) 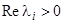 ; 12)
; 12) 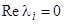 .
.
Если 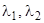 — вещественные (если
— вещественные (если 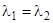 , то должно быть
, то должно быть 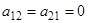 ), то:
), то:
1) 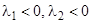 эквивалентно
эквивалентно
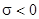 ,
, 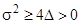 (
(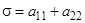 ,
, 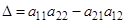 );
);
2) 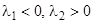 эквивалентно
эквивалентно
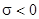 ,
, 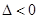 ;
;
3) 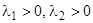 эквивалентно
эквивалентно
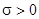 ,
, 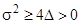 ;
;
4) 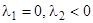 эквивалентно
эквивалентно
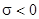 ,
, 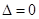 ;
;
5) 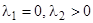 эквивалентно
эквивалентно
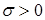 ,
, 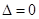 ;
;
6) 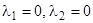 эквивалентно
эквивалентно
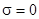 ,
, 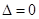 .
.
При 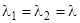 ;
; 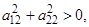
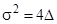 :
:
7) 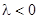 эквивалентно
эквивалентно 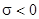 ; 8)
; 8) 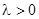 эквивалентно
эквивалентно 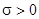 ; 9)
; 9) 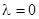 эквивалентно
эквивалентно 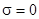 .
.
Наконец, если 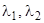 — комплексно-сопряженные,
— комплексно-сопряженные, 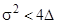 , то:
, то:
10) 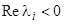 эквивалентно
эквивалентно 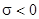 ; 11)
; 11) 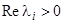 эквивалентно
эквивалентно 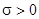 ; 12)
; 12) 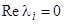 эквивалентно
эквивалентно 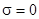 .
.
Приведенная классификация систем по матрице А хоть и грубая, но связана с устойчивостью и неустойчивостью нулевого решения (принципиальная и важная классификация) системы 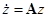 .
.
Не лишне указать алгоритм построения оптимальной матрицы обратной связи для системы уравнений второго порядка (аналогичной будет и общая схема построения таких матриц для произвольных конечномерных систем; технические трудности при этом, естественно, возрастают). После преобразования, канонического по управлению, система общего вида преобразуется к виду:
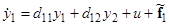
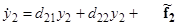 ;
;
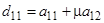 ;
;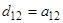 ;
; 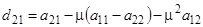 ;
;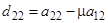 ;
; 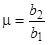 ,
,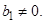
При 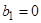 :
: 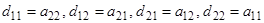 .
.
Параметры 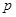 и
и 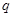 оптимальной матрицы обратной связи
оптимальной матрицы обратной связи 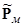
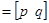 должны выбираться из условий минимума функционала
должны выбираться из условий минимума функционала 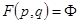 (
(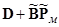 ) (собственные числа матрицы
) (собственные числа матрицы 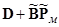 подставляются в функционал Ф [1], а затем p и q выбираются из условия минимума Ф). Имеем:
подставляются в функционал Ф [1], а затем p и q выбираются из условия минимума Ф). Имеем: 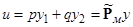 ,
, 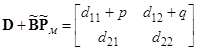 ;
;
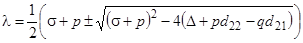 — собственные числа матрицы
— собственные числа матрицы 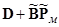 (
(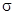 и
и 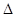 — след и определитель матрицы А совпадают со следом
— след и определитель матрицы А совпадают со следом 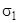 и определителем
и определителем 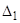 матрицы D, как инварианты при невырожденных преобразованиях координат).
матрицы D, как инварианты при невырожденных преобразованиях координат).
Пришли к задаче минимизации функции 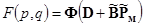 при ограничениях на координаты
при ограничениях на координаты 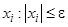 и энергию управляющих воздействий
и энергию управляющих воздействий 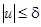 :
:
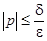 ,
, 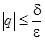 . (6)
. (6)
При выборе р и q величины 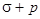 и
и 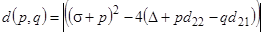 предполагаются наименьшими. Задача легко решается для систем, если коэффициент
предполагаются наименьшими. Задача легко решается для систем, если коэффициент 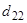 по абсолютной величине мал по сравнению с
по абсолютной величине мал по сравнению с 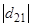 . Алгоритм минимизации функции
. Алгоритм минимизации функции 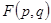 при условии (6) значительно упрощается:
при условии (6) значительно упрощается: 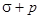 минимизируется при
минимизируется при 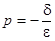 ; если при выбранном q значение
; если при выбранном q значение 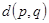 можно сделать равным нулю, то задача решена, если нет, то выбрав шаг
можно сделать равным нулю, то задача решена, если нет, то выбрав шаг 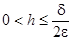 , следует минимизировать
, следует минимизировать 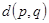 , осуществляя выбор q для значений
, осуществляя выбор q для значений 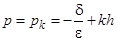 ; k=0,1,2,…, (
; k=0,1,2,…, (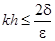 ).
).
Приведенные методики успешно использовались при разработке композиционных материалов специального назначения [4,5].
Литература:
1. A.Danilov, I.Garkina. Systems approach to the modeling and synthesis of building materials Contemporary Engineering Sciences, Vol. 8, 2015, no. 5, 219–225. http://dx.doi.org /10. 12988/ces.2015.517.
2. I.Garkina. Modeling of kinetic processes in composite materials. Contemporary Engineering Sciences, Vol. 8, 2015, no. 10, 421–425. http://dx.doi.org/10.12988/ces.2015.5258.
3. Данилов А. М., Гарькина И. А., Сорокин Д. С. Логико-методологические модели при синтезе композиционных материалов // Региональная архитектура и строительство. — 2015. — № 1(22). — С.23–28.
4. Данилов А. М., Гарькина И. А., Дулатов Р. Л. Ретроспективная идентификация сложных систем // Региональная архитектура и строительство. — 2015. — № 1(22). –С.130 -136.
5. Тюкалов Д. Е., Данилов А. М. Формирование критериев динамического подобия модели реальному объекту / Молодой ученый. — 2015. — № 4(84). — С.278–280.

