В данной работе на примере вязкоупругой пластины рассматриваются задачи динамики тонкостенных конструкций при аэродинамическом нагружении с учетом вязкоупругих свойств материала и геометрической нелинейности. Аэродинамическое давление определяется в соответствии с поршневой теорией А. А. Ильюшина. При помощи метода Бубнова-Галеркина математическая модель задачи сведены к исследованию системы обыкновенных интегро-дифференциальных уравнений (ИДУ). Решение ИДУ находится численным методом, основанным на использовании квадратурных формул. Определена критическая скорость флаттера вязкоупругих пластин при различных физических и геометрических параметрах.

Ключевые слова: теория Тимошенко, математическая модель, интегро-дифференциальные уравнения, метод Бубнова-Галеркина, пластина, флаттер, вязкоупругость.

In the present work the problem about flutter of viscoelastic plates on the basis of Timoshenko's theory taking into account geometrical and aerodynamic nonlinearity is considered. Aerodynamic pressure is defined by A. A. Ilyushin piston theory. By the Bubnov-Galerkin methods, the problems of mathematical model are reduced to investigation of a system of ordinary integro-differential equations (IDE). The IDEs are solved by a numerical method which is based on using the quadrature formulas. Critical speeds of flutter are defined at various physical and mechanical parameters of a viscoelastic plate.

Кey words: theory Timoshenko, mathematical model, integro-differential equations, Bubnov-Galyorkin method, plate, flutter, viscoelastic.

Пусть тонкостенная конструкция с вязкоупругими свойствами материала, радиусом кривизны срединной поверхности R и длиной L, опирающаяся на прямоугольный в плане контур, обтекает с одной стороны сверхзвуковым потоком газа с невозмущенной скоростью V, которая направлена параллельно оси Ох.

Математическая модель данной задачи на основе уточненной теории Тимошенко в геометрически нелинейной постановке, учитывающую деформацию сдвига и инерцию вращения, имеет следующий вид [1]

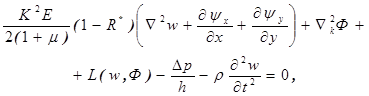                                           (1)

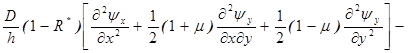
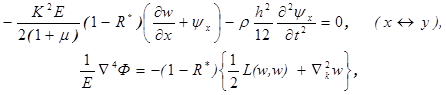
где Dp — избыточное давление.

Если рассматривается линеаризированное течение газа вдоль конструкции, по которой распространяются упругие волны, скорость J приобретает вид (2):

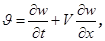
и, следовательно, избыточное давление Dp приобретает вид

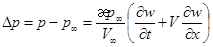.                                                                                 (2)

В случае, когда скорость J имеет нелинейный вид (2)

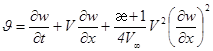,                                                                                 (3)

избыточное давление Dp приобретает вид

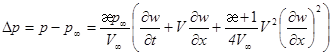,                                                   (4)

где 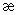 — показатель политропы газа.

Заметим, что система (1) достаточно общая. Она является системой нелинейных интегро-дифференциальных уравнений в частных производных типа Вольтерра. Из нее, в частном случае, можно получить математические модели различных задач.

Без учета радиуса кривизны срединной поверхности (k_x=k_y=0) и при избыточном давлении Dp вида (4) получим математическую модель задачи о флаттере вязкоупругой пластины по уточненной теории Тимошенко с учетом геометрической и аэродинамической нелинейности.

Полученная система решается с помощью метода Бубнова-Галеркина в сочетании с численным методом, основанным на использовании квадратурных формул (3). При расчетах использовалось слабо сингулярное ядро Колтунова-Ржаницына с тремя реологическими параметрами (А, b и a) вида (4)

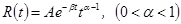                                                                                     (5)

Здесь в качестве критерия, определяющего значения критических скоростей, принимается та скорость, при которой конструкция совершает колебания типа гармонических. Очевидно, что при таких скоростях разложение Бубнова-Галеркина будет сходиться.

Таблица 1

В таблице приводятся численные значения критических скоростей потока газа, полученных без учета геометрической и аэродинамической нелинейностей, с учетом геометрической нелинейности и с учетом геометрической и аэродинамической нелинейностей при различных физических и геометрических параметрах пластины [5–9].

Анализ полученных результатов показывает, что геометрическая нелинейность имеет существенное значение по сравнению с аэродинамической нелинейностью. Согласно таблице результаты линейной и геометрически нелинейной задач отличаются на 25–85 %, в то время как результаты линейной и аэродинамически нелинейной задач во многих случаях почти совпадают. Здесь следует отметить, что влияние аэродинамической нелинейности существенно проявляется при уменьшении параметров d и М_Е.

Также из таблицы наглядно видно, что учет наследственных свойств материала тонкостенной конструкции оказывает существенное влияние на изменения критических скоростей. Надо отметить, что результаты, полученные для случаев без учета и с учетом вязкоупругих свойств материала, отличаются друг от друга на более чем 35–40 %. Заметим также, что увеличение реологического параметра A и уменьшение реологического параметра 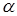 приводят к уменьшению значений критических скоростей. Изменение же третьего реологического параметра b, не оказывает существенного влияния на поведение пластины с вязкоупругими свойствами материала.

Изменение безразмерного параметра жесткости М_Е также играет важную роль в поведении тонкостенной конструкции с вязкоупругими свойствами материала. Как показывают исследования, увеличение этого параметра приводит к интенсивному увеличению критической скорости.

Безразмерный параметр давления М_р наряду с параметром М_Е также играет важную роль. Как и в случае упругой задачи, увеличение этого параметра приводит к интенсивному уменьшению критических скоростей.

Литература:

1.                  Кучаров О. Р. Разработка моделей и методов решения нелинейных задач аэродинамики, описываемых интегро-дифференциальными уравнениями // Узб. журнал «Проблемы информатики и энергетики». — Ташкент, 2010. — № 4. — С.12–16.

2.                  Болотин В. В. Неконсервативные задачи теории упругой устойчивости. — М.: Физматгиз, 1961. — 340 с.

3.                  Бадалов Ф. Б., Эшматов Х., Юсупов М. О некоторых методах решения систем интегро-дифференциальных уравнений, встречающихся в задачах вязкоупругости // Прикладная математика и механика. — Москва, 1981. — № 5 (51). — С. 867–871.

4.                  Колтунов М. А. Ползучесть и релаксация. — М.: Высшая школа, 1976. — 276 с.

5.                  Khudayarov B. A. The Investigation of Flutter of Viscoelastic of Orthotropic Plates. Proceedings of National Academy of Sciences of Armenia: Mechanics. 2010. 2. 63. P.67–77.

6.                  Khudayarov B. A. Numerical Study of the Dependence of the Critical Flutter Speed and Time of a Plate on Rheological Parameters. International Applied Mechanics [Translated from Prikladnaya Mekhanika], Vol.44, No.6, 2008.

7.                  Khudayarov B. A. Flutter of a Viscoelastic in a Supersonic Gas Flow. International Applied Mechanics [Translated from Prikladnaya Mekhanika], Vol.46, No.4, 2010.

8.                  Khudayarov B. A., Mathematical modelling of nonlinear flutter of viscoelastic elements and units of the flying device. Matem. Mod., 2010, Volume 22, Number 6, P. 111–131.

9.                  Khudayarov B. A. Numerical Analysis of the Nonlinear Flutter of Viscoelastic Plates. International Applied Mechanics 41:5, 538–542.