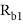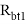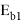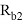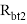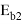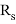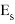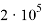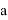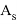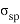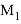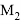Расчет сборно-монолитных железобетонных элементов по прочности на основе нелинейной деформационной модели



В статье автор описывает основы нелинейной деформационной модели железобетона, приводит результаты расчета прочности сборно-монолитной плиты на основе нелинейной деформационной модели и осуществляет сравнение с результатами расчета по методу предельных усилий.

Ключевые слова: нелинейная деформационная модель, сборно-монолитный элемент, предельный изгибающий момент.

Впервые термин «нелинейная деформационная модель» в отечественных нормах появляется в 2003 г. в СНиП 52–01–2003. Затем данное понятие продолжает свое развитие в СП 63.13330.2012 и в актуальном на данный момент СП 63.13330.2018. Кроме того, с 2018 г. был введен в действие СП 337.1325800.2017 «Конструкции железобетонные сборно-монолитные. Правила проектирования», развивающий положения теории применительно к сборно-монолитным железобетонным элементам.

Основой расчетов по нелинейной деформационной модели являются следующие положения [1]:

– выполняется гипотеза плоских сечений, то есть относительные деформации бетона и арматуры в сечении принимаются по линейному закону;

– связь между напряжениями и относительными деформациями бетона и арматуры принимаются в виде диаграмм состояния бетона и арматуры (двухлинейные и трехлинейные диаграммы);

– сопротивление бетона растянутой зоны допускается не учитывать, так как оно незначительно влияет на результаты расчета.

В качестве математических зависимостей, используемых для построения модели, используются:

– уравнения равновесия внешних сил и внутренних усилий в сечении;

– уравнения распределения деформаций по высоте сечения;

– зависимости между напряжениями и относительными деформациями;

– зависимости для построения кусочно-линейных диаграмм материалов.

Для расчета плиты (изгибаемый в одной плоскости элемент) сечение разбивается на отдельные полосы определенной высоты, в пределах которых напряжения принимаются равномерно распределенными.

Критерием прочности при расчете по нелинейной деформационной модели является достижение деформациями бетона или арматуры предельных значений, определяемых в соответствии с [1].

Построение нелинейной деформационной модели производится в программе Microsoft Excel. Преимущества данной программы в том, что она достаточно проста в работе и знакома каждому инженеру и студенту. Кроме того, она позволяет контролировать входные и выходные параметры, что часто бывает скрыто от глаз пользователя в расчетных комплексах.

Расчет будем производить для сборно-монолитной плиты перекрытия. Сечение рассматриваемой плиты состоит из сборного элемента размерами 320х200 мм из бетона B30 и предварительно напряженной арматуры 2ø28 А800, а также бетона омоноличивания толщиной 80 мм из бетона B15. Поперечное сечение плиты приведено на рис. 1.

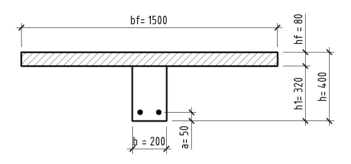
Рис. 1. Сечение рассчитываемой сборно-монолитной плиты

Исходные данные для построения нелинейной деформационной модели сборно-монолитной плиты представлены в таблице 1.

Таблица 1

Исходные данные для построения модели сборно-монолитного сечения по прочности

Показатель	Численное значение
Расчетное сопротивление бетона сборного элемента на сжатие , МПа	17
Расчетное сопротивление бетона сборного элемента на растяжение , МПа	1,15
Модуль упругости бетона сборного элемента , МПа	32500
Расчетное сопротивление бетона омоноличивания на сжатие , МПа	8,5
Расчетное сопротивление бетона омоноличивания на растяжение , МПа	0,75
Модуль упругости бетона омоноличивания , МПа	24000
Расчетное сопротивление арматуры на растяжение , МПа	695
Модуль упругости арматуры , МПа
Защитный слой бетона , мм	50
Площадь армирования , см 2	12,31
Величина предварительного напряжения, , МПа	520
Изгибающий момент на первой стадии , кНм	25
Изгибающий момент на второй стадии , кНм	263

Расчет сборно-монолитной плиты в соответствии с [2] ведется в две стадии. Поперечное сечение плиты разбиваем на слои высотой 2 мм.

Для построения модели используем двухлинейную диаграмму для бетона и трехлинейную диаграмму для арматуры.

Расчет для первой стадии работы

На первой стадии рассчитываем сборный элемент на действующий момент (от собственного веса сборного элемента и бетона омоноличивания). Целью расчета является определение относительных деформаций в бетоне и арматуре сборного элемента.

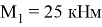
Вычисленные относительные деформации бетона и арматуры используем при расчете по второй стадии.

Расчет для второй стадии работы

На второй стадии рассматривается цельное сборно-монолитное сечение (сборный элемент и бетон омоноличивания работают совместно). Цель расчета: определение предельного изгибающего момента, воспринимаемого поперечным сечением сборно-монолитной плиты.

Предельный изгибающий момент, определенный по нелинейной деформационной модели, составляет 294,03 кНм.

Определение предельного изгибающего момента по предельным усилиям

Определим предельный изгибающий момент по формулам свода правил [2] и сравним полученные результаты.

Рассматриваемое сечение плиты представляет собой тавровое сечение с полкой из монолитного бетона. Такое сечение рассчитываем в соответствии с п. 5.1.13 [2].

Определяем границу сжатой зоны бетона, от этого зависит способ расчета. Проверим выполнение условия:

(1)

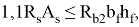
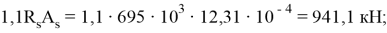
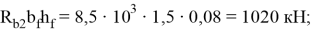
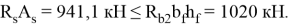
Условие выполняется, т. е. граница сжатой зоны проходит в полке и расчет производим как для прямоугольного сечения шириной . Расчетное сечение принимается выполненным из одного (монолитного) бетона.

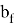
Высоту сжатой зоны определяем по формуле:

(2)

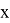
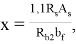
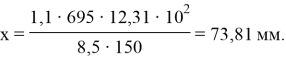
Предельный изгибающий момент, воспринимаемый сборно-монолитным сечением, вычислим по формуле:

(3)

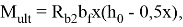
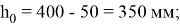
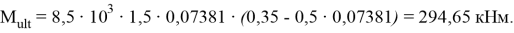
Определение предельного изгибающего момента по трехлинейной диаграмме и с учетом растянутого бетона

Дополнительно определим предельный изгибающий момент, используя трехлинейную диаграмму бетона и работу растянутого бетона. Все полученные результаты расчетов сведем в таблицу 2 для сравнения.

Таблица 2

Сравнение результатов определения предельного изгибающего момента

Расчет	Численное значение, кНм	Разница с расчетом по предельным усилиям, %
По предельным усилиям	294,65	-
По НДМ (двухлинейная диаграмма сжатого бетона)	294,03	-0,21
По НДМ (трехлинейная диаграмма сжатого бетона)	293,72	-0,32
По НДМ (трехлинейная диаграмма сжатого и растянутого бетона)	293,71	-0,32

Расхождение результатов, полученных по нелинейной деформационной модели, с результатами по методу предельных усилий достаточно невелики, что свидетельствует о правильности построенной модели. В ходе исследования было подтверждено, что в нелинейной деформационной модели при расчете по прочности допускается не учитывать работу растянутого бетона (полученная разница результатов попадает в пределы математической погрешности). Также сделан вывод о том, что для описания напряженно-деформированного состояния сжатого бетона наиболее целесообразным является применение двухлинейной диаграммы, так как она проще в математическом описании, а разница в расчете по двухлинейной и трехлинейной диаграммам не столь велика (около 0,1 %, что пренебрежимо мало).

Исследование работы конструкции

Эпюра распределения напряжений в сечении рассматриваемой сборно-монолитной плиты при достижении верхней гранью сечения деформаций, соответствующих предельной деформации бетона сжатию, представлена на рис. 2.

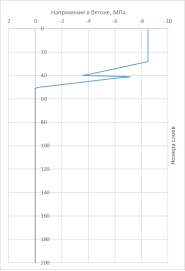
Рис. 2. Эпюра напряжений в бетоне сборно-монолитного элемента

На эпюре можно выделить три характерных участка:

– сжатая зона бетона омоноличивания (слои 1–40). При этом напряжения в слоях 1–28 достигают расчетного сопротивления бетона омоноличивания на сжатие ;

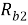
– сжатая зона бетона сборного элемента (слои 41–50), в которой напряжения не достигают предела прочности бетона сборного элемента на сжатие;

– растянутая зона бетона сборного элемента (слои 51–200).

Для исследования работы конструкции и анализа напряженно-деформированного состояния построим график в осях «Кривизна» -«Изгибающий момент» (рис. 3).

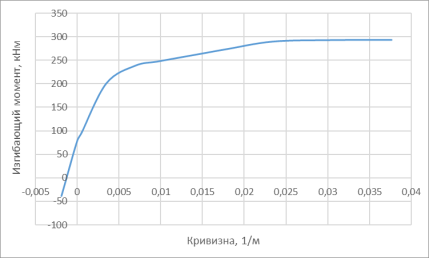
Рис. 3. График зависимости момента от кривизны

На данном графике можно выделить три участка:

1. Первый участок характеризуется наибольшим углом наклона графика к оси кривизны, что в данных соответствует наибольшей жесткости элемента.
2. Второй участок обусловлен появлением нормальных трещин в элементе и вследствие этого снижением жесткости сборно-монолитного элемента. Начало участка соответствует моменту образования трещин.
3. Третий участок — образование пластического шарнира в элементе — рост деформаций без увеличения внешней нагрузки.

Таким образом, данное исследование показало, что расчет прочности сборно-монолитного элемента по нелинейной деформационной модели показывает достоверные результаты и небольшое расхождение с расчетом по методу предельных усилий. Однако явным преимуществом нелинейной деформационной модели является возможность анализировать напряженно-деформированное состояние конструкции в любой момент времени.

Литература:

1. СП 63.13330.2018 Бетонные и железобетонные конструкции. Основные положения.
2. СП 337.1325800.2017 Конструкции железобетонные сборно-монолитные. Правила проектирования.