Анализ состояния проблемы проектирования систем управления сложными технологическими объектами показывает, что традиционные методы построения моделей объектов и систем управления ими не приводят к удовлетворительным результатам, когда исходное описание подлежащей решению проблемы заведомо является неточным и неполным [1,2,6,8]. Известно, что слабоструктурированные или плохо определенные объекты обладают такими свойствами, как нестационарность параметров, неполнота информации, отсутствие формального описания объекта управления и др. [1,7,11]. В этих случаях целесообразным является использование методов интеллектуального управления, позволяющих учитывать неполноту и неточность исходных данных.
Рассмотрим химический реактор входными параметрами, которого являются: расход пара и обессоленной воды; начальная температура в рубашке и реакторе; начальная концентрация компонентов реакционной смеси. Остальные воздействия являются возмущающими, в качестве основного возмущающего воздействия можно принять давление греющего пара.
Входным регулирующим воздействием для температуры реактора является расход греющего пара, а остальные воздействия являются возмущающими [3,8].
Одним из важнейших параметров, характеризующих качество технологического процесса, является концентрация и рабочая вязкость прядильного раствора на выходе реактора. Измерение данных параметров возможно только лабораторным путем. Анализ литературных источников [3,7,8] и опыт промышленной эксплуатации показали, что для получения прядильного раствора заданного качества необходимо поддерживать определенный температурный режим. Поэтому в качестве выходного параметра выбирается температура реактора 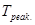 . Температура реактора, в свою очередь, является управляемым параметром, и она управляется с помощью температуры рубашки реактора
. Температура реактора, в свою очередь, является управляемым параметром, и она управляется с помощью температуры рубашки реактора 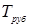 .
.
При наличии на объекте внешних или параметрических возмущающих воздействий (например, изменение давление пара более чем на 15 %, изменение концентрация компонентов реакционной смеси на 10 %), существенно ухудшаются качественные показатели переходного процесса, что может привести систему управления к неустойчивому состоянию.
Поэтому решение подобных задач предлагается искать с применением теории нечеткой логики, позволяющей оперировать лингвистическими нечеткими высказываниями. Таким образом, ставится задача синтеза робастной нечеткой системы управления температурным режимом химического реактора, инвариантной к внешним и параметрическим возмущениям.
Для решения поставленной задачи на основе предлагаемого подхода рассмотрим замкнутую систему автоматического регулирования температуры химического реактора с нечетким логическим контроллером (НЛР)
На нечеткий регулятор возлагается задача выработки управляющего воздействия в диапазоне изменения динамической ошибки регулирования и ее производной относительно ее пороговых значений. Входной вектор НЛР преобразуется в нечеткую форму 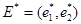 с помощью блока фаззификации, затем выполняется нечеткий логический вывод в базе правил, в результате чего получается нечеткая выходная переменная
с помощью блока фаззификации, затем выполняется нечеткий логический вывод в базе правил, в результате чего получается нечеткая выходная переменная 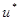 . Перевод значений вектора управления
. Перевод значений вектора управления 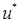 из нечеткой области в четкую
из нечеткой области в четкую 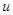 осуществляются блоком дефаззификации.
осуществляются блоком дефаззификации.
Предобработка входного сигнала ошибки регулирования и ее производной осуществляется по формуле:
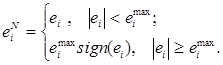
Постобработка выходного управляющего сигнала 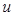 осуществляются решением задачи денормализации
осуществляются решением задачи денормализации 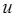 :
:
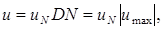
где 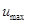 — максимальное значение управления, подаваемого объект.
— максимальное значение управления, подаваемого объект.
Как правило, база знаний НЛР содержит описание термов лингвистический переменных (ЛП), которые должны быть определены заранее для каждой входной и выходной переменной.
Для этого введем следующие лингвистические переменные 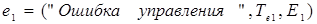 ,
, 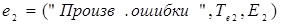 и
и 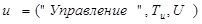 , где
, где 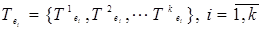 ,
, 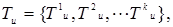 — терм-множества значений лингвистических переменных
— терм-множества значений лингвистических переменных 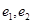 и
и 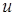 с соответствующими функциями принадлежности (ФП)
с соответствующими функциями принадлежности (ФП) 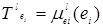 ,
, 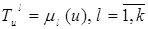 , заданными соответственно на универсальных множествах
, заданными соответственно на универсальных множествах 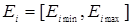 и
и 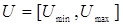 .
.
Предположим, что каждой входной и выходной лингвистической переменной 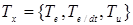 соответствуют 7 термов:
соответствуют 7 термов: 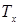 ={‘NB’,’NM’,’NS’,’ZE’,’PS’,’PM’,’PB’} с треугольными функциями принадлежностями:
={‘NB’,’NM’,’NS’,’ZE’,’PS’,’PM’,’PB’} с треугольными функциями принадлежностями:
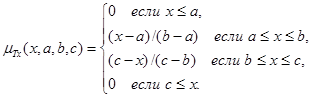 .
.
Тогда результатом фаззификации являются лингвистические переменные:
e1,=«Ошибка» = [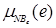 /NBe,
/NBe,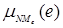 /NMe,
/NMe,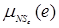 /NSe,
/NSe,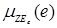 /ZEe,
/ZEe, 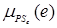 /PSe,
/PSe,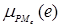 /PMe,
/PMe,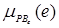 /PBe];
/PBe];
e2=«Скорость изменения ошибки» = [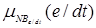 /NBe/dt,
/NBe/dt, 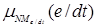 /NMe/dt,,
/NMe/dt,, 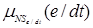 /NSe/dt,
/NSe/dt,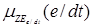 /ZEe/dt,
/ZEe/dt,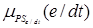 /PSe/dt,
/PSe/dt, 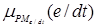 /PMe/dt,
/PMe/dt, 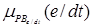 /PBe/dt];
/PBe/dt];
u*=«Управление» = [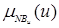 /NBu,
/NBu,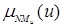 /NMu,
/NMu,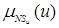 /NSu,
/NSu,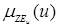 /ZEu,
/ZEu, 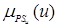 /PSu,
/PSu, 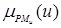 /PMu,
/PMu,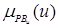 /PBu].
/PBu].
Далее формируем базы правил логического вывода НЛР в виде:
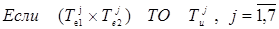 ,
,
где 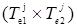 - декартово произведение нечётких множеств E1 и E2, заданных на шкалах E1 и E2, с функцией принадлежности:
- декартово произведение нечётких множеств E1 и E2, заданных на шкалах E1 и E2, с функцией принадлежности:
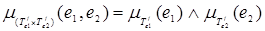 ,
,
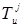 — соответствующее выходное нечёткое множество, определяемое нечётким отношением
— соответствующее выходное нечёткое множество, определяемое нечётким отношением 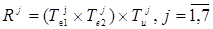 с функцией принадлежности:
с функцией принадлежности:
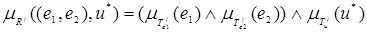 .
.
Совокупность всех правил, соответствующих нечёткому отношению 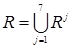 с функцией принадлежности
с функцией принадлежности
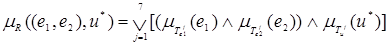 ,
,
определяет базу знаний НЛР и задает закон функционирования нечёткой системы.
Таким образом, при заданных значениях входных лингвистических переменных 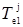 и
и 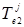 выходное значение нечетко-логического регулятора
выходное значение нечетко-логического регулятора 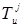 можно определить на основе следующего композиционного правила [9]:
можно определить на основе следующего композиционного правила [9]:
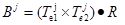
со степенью принадлежности:
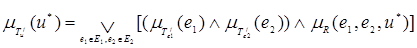 .
.
В случае, когда лингвистическим переменным входных сигналов 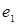 и
и 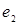 соответствуют нечёткие множества
соответствуют нечёткие множества 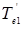 и
и 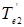 , нечёткое множество
, нечёткое множество 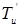 лингвистической переменной сигнала управления u* определяется следующим образом:
лингвистической переменной сигнала управления u* определяется следующим образом:
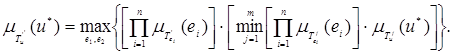
Для получения реального значения выходного сигнала нечёткого регулятора осуществляется процесс дефаззификации [11]:
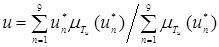 .
.
Функцию принадлежности нечеткого значения 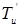 можно представить в виде:
можно представить в виде:
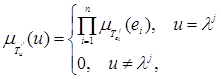 ,
,
где 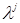 — дискретные численные значения выходного сигнала.
— дискретные численные значения выходного сигнала.
Тогда определяющее значение выходного сигнала НЛР на этапе дефаззификации можно вычислить следующим образом:
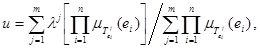
или 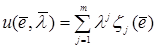 ,
,
где 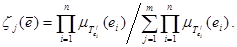
Таким образом, в случае полноты и непротиворечивости базы правил нечеткого логического вывода, закон функционирования НЛР определяется видом и распределением по диапазону регулирования функций принадлежности и выбранным алгоритмом нечёткого вывода.
Рассмотренный алгоритм синтеза нечетко-логического регулятора отличается простотой, поскольку позволяет использовать стандартную форму описания лингвистических переменных и минимальный набор управляющих правил. Синтезированный нечеткий логический регулятор придает системе автоматического регулирования способность поддерживать на заданном уровне температуры реактора при наличии внешних возмущений, а также качественно управлять технологическим процессом полимеризации при широком диапазоне изменения его параметров во времени.
Литература:
2. Васильев В. И., Ильясов Б. Г. Интеллектуальные системы управления: Теория и практика. — М.: Радиотехника, 2009. — 392 с.
3. Голдинг Б. Химия и технология полимеров. М.: Издатинлит, 1973. — 357 с.
4. Гостев В. И. Проектирование нечетких регуляторов для систем автоматического управления — СПб.: БХВ-Петербург, 2011. — 416 с.
5. Интеллектуальные системы автоматического управления / Под ред И. М. Макарова, В М Лохина — М ФИЗМАТЛИТ, 2001–576 с — ISBN 5–9221–0162–5.
6. Пегат А. Нечеткое моделирование и управление. М.: Бином. Лаборатория знаний, 2009. — 798 с.
7. Ульянов С. В., Литвинцева Л.В и др. Интеллектуальное робастное управление: технологии мягких вычислений. –М.: ВНИИгеосистем, 2011.-408 с.
8. Mamdani E. H. Rule-based Fuzzy Approach to the Control of Dynamic Processes II IEEE Trans, on Comput. — 1981. — № 12. — P. 432–440.
9. Rotach V. The Analysis of Traditional and Fuzzy PID Rigulators. Proceeding 8-th Zittau Fuzzy Colloquium, 2000. — P. 165–172.
10. Zadeh L. Fuzzy logic, neural network and soft computing. Communications of the ACM. -1994. -Vol. 37. — № 3. — P. 30–39.
11. Zimmerman Y. J. Fuzzy set Theory and its applications. Second Revised Edition, 1990. — 398 p.

