В статье приведены математические алгоритмы обработки низкочастотных сигналов на основе вейвлет-преобразований Добеши и Морле. Представлена технология снятия сигналов с коры головного мозга человека. Анализируется обработанный низкочастотный сигнал на формирование управляющего сигнала для интеллектуального тренажера.
Ключевые слова: низкочастотный сигнал, анализ сигнала, обработка сигнала, программирование, вейвлет-преобразование, вейвлет Добеши, вейвлет Морле.
На сегодняшний день существуют разнообразные программные обеспечения, которые позволяют осуществлять различные сложные преобразования звукового сигнала. Механизмы цифровой обработки сигнала выполняются как на программном, так и на аппаратном уровне. Но все эти программные средства не предназначены для работы с низкочастотными сигналами коры головного мозга человека.
При обработке низкочастотного сигнала необходимо учитывать его фазовую или частотную характеристики, расширение или сужение динамического диапазона, применение частотной, амплитудной или фазовой модуляции, а также устранение шумов/помех.
Цель работы — выбор оптимальных параметров вейвлет-преобразования Добеши и Морле, определение шага масштаба и временного интервала между отсчетами сдвига вейвлет-преобразования применительно к обработке низкочастотных сигналов для формирования управляющих сигналов.
Напряжение в точке соприкосновения электрода с поверхностью кожи головы определяет сумму напряжений, локализированные в радиусе этого электрода [1]. Подобные колебания напряжений называются суммой колебаний напряжений с разных локализированных участков кожного покрова, костной ткани или коры головного мозга (рис. 1).
Дополнительные наводки низкочастотных сигналов различной частоты и амплитуды имеют следующий вид (1) [2]:
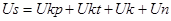 , (1)
, (1)
где 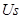 — суммарное изменение потенциальной энергии, приходящееся на единицу заряда;
— суммарное изменение потенциальной энергии, приходящееся на единицу заряда;
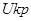 — изменение потенциальной энергии кожного покрова;
— изменение потенциальной энергии кожного покрова;
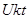 — изменение потенциальной энергии костной ткани;
— изменение потенциальной энергии костной ткани;
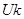 — изменение потенциальной энергии коры головного мозга.
— изменение потенциальной энергии коры головного мозга.
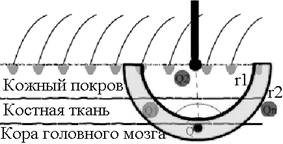
Рис. 1. Модель снятия сигнала с кожного покрова головы
Методы обработки низкочастотных сигналов коры головного мозга основаны на разнообразных закономерностях. Таким образом, функция вейвлет-преобразования 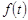 будет иметь следующим вид (2) [3]:
будет иметь следующим вид (2) [3]:
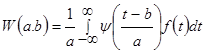 , (2)
, (2)
где 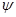 — функция вейвлета;
— функция вейвлета;
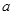 — момент времени;
— момент времени;
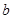 — параметр обратный частоте;
— параметр обратный частоте;
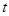 — ось времени.
— ось времени.
Изменяющаяся базисная частота влияет непосредственно на основные характеристики вейвлет-преобразования. Однако, метод вейвлет-анализа свободен от различных погрешностей. Отсюда вытекает следующая интерпретация (3):
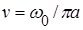 , (3)
, (3)
где 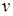 — частотная переменная обратного приведенного масштаба.
— частотная переменная обратного приведенного масштаба.
Основной модуль вейвлет-преобразования представлен в виде определенного дифференциального уравнения (4):
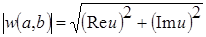 . (4)
. (4)
Разрабатываемый программный комплекс САЗСМЧ (спектральный анализ звуковых сигналов мозга человека) (рис. 2) оснащен несколькими программными алгоритмами на основе вейвлет-преобразования Добеши (5) [4] и Морле (6) [5, 6], которые разработаны специально для обработки низкочастотных сигналов частотой в диапазоне от 10 до 50 Гц. Структурная модель математического алгоритма вейвлет-преобразования представлена на рис. 3 [7].
Рис. 2. Загрузочный логотип программы САЗСМЧ
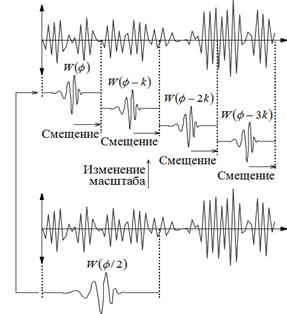
Рис. 3. Структурная модель математического алгоритма вейвлет-преобразования
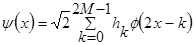 , (5)
, (5)
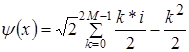 , (6)
, (6)
где 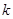 — целочисленные трансляции;
— целочисленные трансляции;
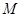 — определяет число коэффициентов функции вейвлета;
— определяет число коэффициентов функции вейвлета;
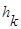 — длина области вейвлета.
— длина области вейвлета.
При обработке низкочастотного сигнала необходимо разложить его в вейвлет-ряд. Так при анализе полученных данных будет проще формировать управляющие сигналы. Для этого следует применить следующее равенство (7) [8]:
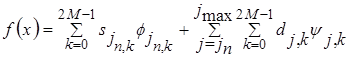 , (7)
, (7)
где 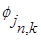 — масштабированная версия масштабной функции
— масштабированная версия масштабной функции 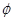 ;
;
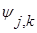 — смещенная версия «материнского» вейвлета
— смещенная версия «материнского» вейвлета 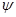 ;
;
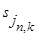 — коэффициенты аппроксимации;
— коэффициенты аппроксимации;
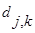 — детализирующие коэффициенты.
— детализирующие коэффициенты.
Для первоначальной обработки низкочастотного сигнала будет применено частотно-временное уравнение (8):
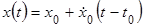 , (8)
, (8)
где 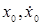 — неизвестные параметры низкочастотного сигнала;
— неизвестные параметры низкочастотного сигнала;
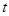 — текущий момент времени;
— текущий момент времени;
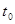 — начальный момент времени (9):
— начальный момент времени (9):
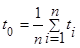 . (9)
. (9)
С помощью разработанных алгоритмов вейвлет-преобразования Добеши и Морле была произведена обработка снятого низкочастотного сигнала с коры головного мозга человека [9]. Полученная синусоидальная кривая низкочастотного сигнала представлена на рис. 4.
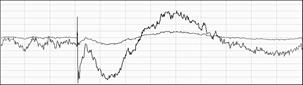
Рис. 4. Синусоидальная кривая низкочастотного сигнала
Полученные данные были избыточны, т. е. на всем промежутке сигнала преобладали разнообразные шумы/помехи. В начале графика (рис. 4) до начала обработки сигнала (3 первых сегмента) присутствуют отчетливые шумы/помехи, которые в процессе всей обработки затрудняют получить конечные точные результаты. Для того чтобы избавить низкочастотный сигнал от присутствия шумов/помех следует применить аппаратный или программный фильтр и произвести повторную обработку снятого сигнала.
Для дальнейшего проведения исследования будет использован разработанный алгоритм программного линейного фильтра с дискретным временем [10], результаты которого показаны на рис. 5.
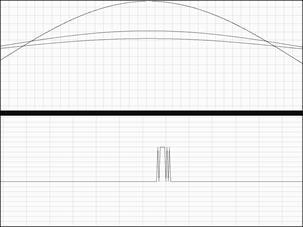
Рис. 5. Пример формирования управляющего сигнала для переключения схемы управления тренажером
Отфильтрованный низкочастотный сигнал позволил сформировать управляющий сигнал, показанный в нижней части рис. 5. Полученный управляющий сигнал будет служить для определенно-заданных команд управления интеллектуальным тренажером.
По результатам полученных данных был реализован метод обработки управляющих сигналов коры головного мозга с датчиков электроэнцефалограммы, основанный на снижении или уменьшении бета-сигналов с параметрами амплитуды менее 5–15 мкВ для частот 10–50 Гц в области центральных лобных извилин, задних центральных и лобных извилины. Это связано с тем, что бета-ритм связан с соматическими сенсорными и двигательными корковыми механизмами, что позволяет достичь реакцию угасания на двигательную активацию или тактильную стимуляцию. Для мю-ритмов амплитуда нарастает до 50 мкВ при двигательной активации или соматосенсорной стимуляции для частот 8–13 Гц.
Литература:
1. Бибиков Д. В., Буров Р. Б., Лавлинский В. В., Табаков Ю. Г. Метод проектирования схем для считывания НЧ-сигналов с коры головного мозга // Моделирование систем и процессов. –2013. –№ 2. –С. 11–14.
2. Бибиков Д. В., Буров Р. Б., Лавлинский В. В., Табаков Ю. Г. Исследование подходов для создания информационной составляющей при проектировании интеллектуального тренажера на основе сигналов коры головного мозга // Моделирование систем и процессов. –2012. –№ 4. –С. 52–56.
3. Табаков Ю. Г., Лавлинский В. В. Бибиков Д. В. Метод и алгоритм обработки НЧ сигналов с помощью вейвлета Добеши // Моделирование систем и процессов. –2014. –№ 3. –С. 42–44.
4. Бибиков Д. В., Буров Р. Б., Лавлинский В. В., Табаков Ю. Г. Вейвлет-преобразование Добеши для низкочастотных сигналов, снятых с коры головного мозга человека // Моделирование систем и процессов. –2013. –№ 2. –С. 8–11.
5. Табаков Ю. Г., Бибиков Д. В. Анализ вейвлет-преобразования Морле для снятия и обработки НЧ сигналов // Системы управления и информационные технологии. –2014. –№ 3.2(57). –С. 272–275.
6. Бибиков Д. В., Лавлинский В. В., Табаков Ю. Г. Модифицированный алгоритм вейвлет-преобразования Морле для анализа НЧ сигналов // Моделирование систем и процессов. –2013. –№ 3. –С. 12–14.
7. Табаков Ю. Г., Лавлинский В. В. Бибиков Д. В. Оптимизация алгоритмов вейвлет-преобразования при моделировании НЧ сигналов // Моделирование систем и процессов. –2014. –№ 3. –С. 47–49.
8. Лавлинский В. В., Табаков Ю. Г. Анализ вейвлет-преобразований Добеши и Морле на малейшие изменения в НЧ сигнале // Научный вестник Воронежского государственного архитектурно-строительного университета. Серия: Информационные технологии в строительных, социальных и экономических системах. –2014. –№ 2. –С. 56–59.
9. Табаков Ю. Г., Лавлинский В. В. Рационализация выбора математических алгоритмов для управляющих НЧ сигналов // Моделирование систем и процессов. –2014. –№ 3. –С. 39–41.
10. Табаков Ю. Г., Лавлинский В. В. Бибиков Д. В. Обработка НЧ сигналов для интеллектуальных тренажеров с применением программных линейных фильтров с дискретным временем // Моделирование систем и процессов. –2014. –№ 3. –С. 45–47.

