Статья посвящена изучению аварийных и рабочих режимов работы тяговой сети постоянного тока с помощью функций в среде MATLAB; нахождению различий и адаптации к изменяющимся условиям с помощью искусственного интеллекта. Рассмотрена возможность построения и применения нейронной сети в релейных защитах питающих линий тяговой сети постоянного тока [1].
Ключевые слова: тяговая сеть, аварийный режим, рабочий режим, искусственный интеллект.
Электротехническое оборудование, используемое на тяговых подстанциях, требует применения защитных систем (имеется устоявшийся термин «релейная защита», хотя на сегодняшний день реализация микропроцессорная), чтобы дорогостоящая техника не выходила из строя из-за нередко случающихся перегрузочных, нештатных и аварийных режимов. Так как любое присоединение к шинам тяговых подстанций должно быть защищено от подобных режимов, наиболее распространенной является защита питающих линий тяговой сети электрифицированных железных дорог. Наибольшую сложность в классификации режимов работы представляют собой питающие линии тяговых подстанций постоянного тока. Сложность заключается в схожести процессов изменения тока питающей линии при рабочих, перегрузочных, нештатных и аварийных режимах. В случае появления режима отличного от рабочего, защищаемое устройство должно быть отключено, но нередко процесс может быть лишь очень похожим на аварийный, а на самом деле не являться таковым. В таком случае возникает задача научится правильно выявлять нерабочие режимы.
Существующие микропроцессорные защиты питающих линий тяговой сети постоянного тока (ЦЗАФ-3,3; ИнТер-3,3; БЗ-М1 и др.) производят анализ тока по одной точке (максимальная токовая защита), по двум точкам (защита по критической скорости нарастания тока) или по трём точкам (защита по приращению тока с анализом развития процесса изменения тока после определения нарастания тока, превышающего уставку). Это безусловно лучше, чем работа реле-дифференциального шунта совместно с быстродействующим выключателем, но все еще недостаточно для однозначного определения нерабочего режима. Необходимо производить анализ бόльших временных последовательностей. На современном этапе развития систем обработки сигналов и решения задач идентификации и кластеризации наилучшим решением является применение нейронных сетей и искусственного интеллекта. Поэтому необходимо исследовать реальные замеры токов питающей линии тяговой подстанции и выявить характерные особенности, аномалии, признаки различных режимов работы, построить интеллектуальную защиту и обучить её нейронную сеть.
Для анализа токов питающей линии будем использовать результаты реальных измерений на фидере одной из действующих тяговых подстанций Московского метрополитена (рисунок 1). Сам анализ будем производить в самой популярной инженерной среде MATLAB. Последовательно рассмотрим функции анализа сигналов от простых к более сложным. Примеры команд будем приводить исходя из того, что сигнал считан в переменную If311 . Ток и напряжение записаны с шагом дискретизации 1 мс.
Самой простой обработкой является нахождение экстремальных и средних значений сигнала [2].
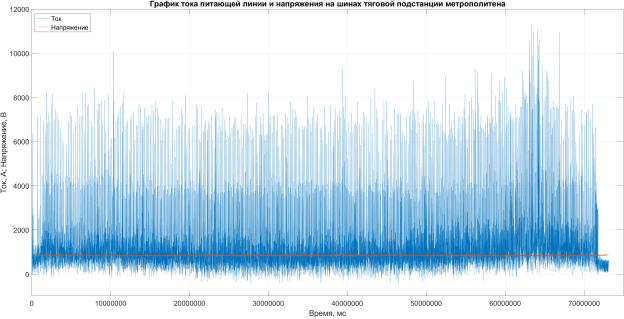
Рис. 1. График тока и напряжения питающей линии тяговой подстанции постоянного тока одной из действующих подстанций Московского метрополитена
Min=min(If311); — нахождение минимального значения тока фидера;
Max=max(If311); — нахождение максимального значения тока фидера;
Cp=mean(If311); — нахождение среднего значения тока фидера;
CK=rms(If311); — нахождение среднеквадратичного значения тока фидера;
PR=max(diff(If311)); — нахождение значения максимальной скорости изменения сигнала (производной сигнала). Значение получается в А/мс;
При выполнении указанных команд будут выведены следующие результаты:
Min = -448.225880172305
Max = 11284.7456890439
Cp = 1492.5495196244
CK = 2027.6383070517
PR = 500.95833666317
Одной из простых обработок сигнала является нахождение средней величины на интервале с постоянным временным периодом, который постоянно смещается на величину шага дискретизации. Такой вид обработки получил название вычисление скользящего среднего. Результатом является функция от времени.
MV=movmean(If311,1000*60*60); — нахождение скользящего среднего
Работа релейных защит основана на анализе переходных процессов. Одной из характеристик переходного процесса является постоянная времени электрической цепи. Исходя из особенностей системы тягового электроснабжения с преимущественно индуктивным характером электрической схемы замещения, можно с некоторым приближением описать контур тока фидера следующим выражением [3]:
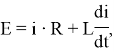
где
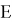
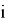
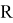
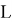
Решение данного дифференциального уравнения можно записать в следующем виде:
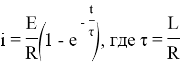
Для определения постоянной времени
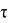
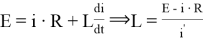
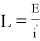
indx=find(If311==0); поиск значений равных нулю
indx1=find(If311~=0); — поиск значений не равных нулю
Utp0=U(indx);
Utp0max=max(Utp0);
L=Utp0max/PR;
R=mean(U(indx1)./If311(indx1));
tau=L/R;
Результат оценки постоянной времени электрической цепи исследуемого фидера:
tau = 1.60915082151614
Дальнейший анализ сигнала должен строится на выделении временных интервалов с характерными, значимыми изменениями тока фидера. Такой анализ можно производить на основе поиска пиковых значений. Выявление всех пиков производиться следующими командами:
Ipeaks=If311(1:1000*60*60);
Peak1=findpeaks(Ipeaks);
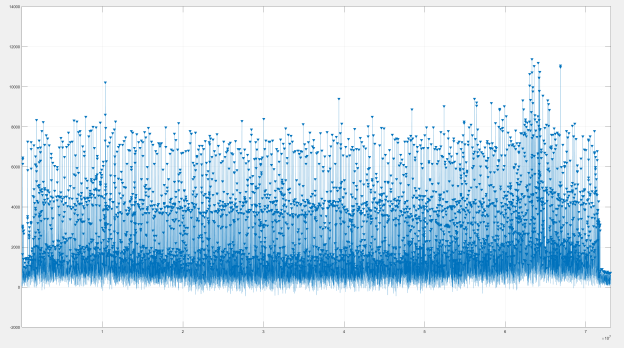
Рис. 2. График всех пиков часового сигнала тока фидера
Для увеличения скорости обработки исследуется не весь сигнал, а только 1 час. Результат нахождения всех пиков представлен на рисунке 2.
Очевидно, что не все скачки тока являются аварийными, и среди них необходимо выделить максимальные. Для выделения нужных пиков используются дополнительные параметры функции findpeaks: MinPeakProminence — выделяет самые высокие и самые низкие пики на графике и MinPeakDistance — убирает все пики, которые находились на одном уровне с центральным пиком, т. е. убирает некий “шум”. Модифицированный поиск пиков выглядит следующим образом:
[p1,locs]=findpeaks(Ipeaks,'MinPeakProminence',120,'MinPeakDistance',160);
После применения данной команды, из графика, содержащего все пики, получаем диаграмму тока с пиками, нужными нам (рисунок 3).
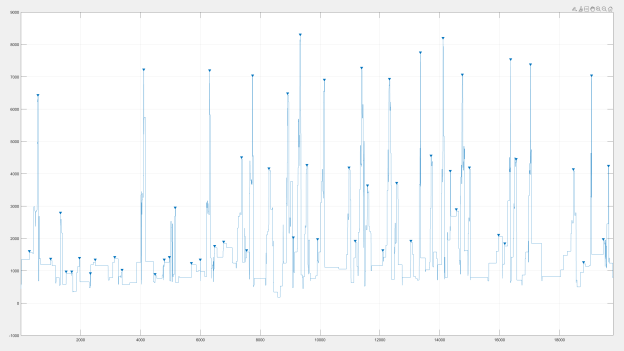
Рис. 3. График отфильтрованных пиков тока фидера
Для обучения нейронной сети, поиска аномальных пиков, построения кластеризации пиков на основе диаграммы соседних связей необходимо выделить временные последовательности сигнала тока одинаковой длины с центром в найденном пике. Это можно реализовать следующей последовательностью команд:
M=zeros(length(locs), 20001);
for i=1:length(locs)
M(i,:)=If311(locs(i)-10000:locs(i)+10000,1);
end
figure
hold on
for i=1:size(M,1)
plot(M(i,:))
end
hold off
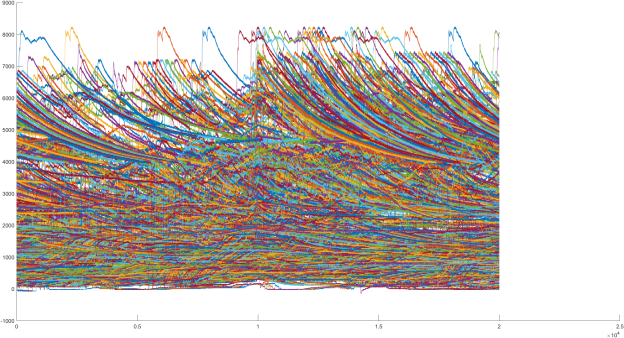
Рис. 4. Генеральная совокупность временных последовательностей тока филера на основе выделенных характерных пиков
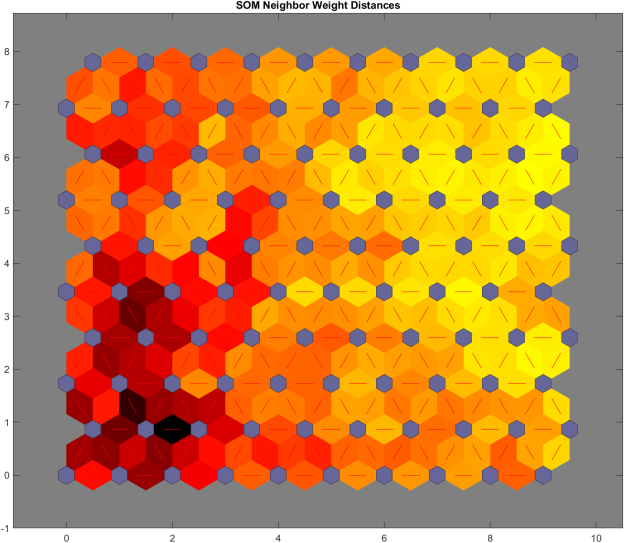
Рис. 5. Диаграммы соседних связей
С помощью среды MATLAB произведен анализ сигнала тока фидера тяговой подстанции метрополитена. Установлены характеристические параметры сигнала в целом и параметры переходных процессов. Удалось выделить генеральную совокупность временных последовательностей тока филера для дальнейшего обучения нейронной сети и получить диаграмму соседних связей, посредством которой появилась возможность классифицировать изменения токов на принадлежность к аварийными, перегрузочным, рабочим и нештатным процессам.
Литература:
- Бредихин Я. В., Лечкин И. О., Кокушкин Р. В. О проверке кратности чисел в двоичной системе счисления и реализации схем проверки в среде matlab/simulink / Я. В. Бредихин. — Издательство Молодой ученый, Москва. 2020. — С. 22–26
- Андреев В. В., Гречишников В. А., Заторская Л. П. Методические указания к лабораторным работам в дисплейном классе по дисциплине «магистральные электрические железные дороги» / В. В. Андреев. — Типография МИИТа. Москва, ГСП-4. 2022
- Солонина А. И., Клионский Д. М., Меркучева Т. В., Перов С. Н. Цифровая обработка сигналов и MATLAB. / А. И. Солонина. — СПб.: БХВ-Петербург, 2013. — 512 с.: ил.— (Учебная литература для вузов)

