Формирование системы знаний в математике предполагает выстраивание изученного материала в сжатую, с логической точки зрения, структурную систему; осознание взаимосвязей между отдельными вопросами, разделами того или иного курса и смежными курсами; овладение студентами методологическими знаниями, и, в частности, средствами познания, обеспечивающими возможность актуализации развивающего компонента обучения. Иными словами, необходимо наметить некоторые ориентиры для характеристики усваиваемой совокупности знаний, наличие которых позволит нам считать эту совокупность систематизированными знаниями.
Необходимым компонентом систематизации знаний является диагностика ее уровня, на основе которой можно проводить корректное целеполагание, планирование, управление дальнейшей работой и ее рефлексию при обучении той или иной дисциплине.
В основу такой диагностики нами была положена следующая иерархия уровней систематизации знаний, которые раскрываются ниже на примере математического содержания:
Уровень фрагментарных знаний: он характеризуется знанием отдельных компонентов системы, отсутствием у учащихся понимания места элементов в системе, необходимых связей между ними. Математическая деятельность, направленная на усвоение знаний, реализуется с помощью действий. Всякое действие, в свою очередь, осуществляется с помощью математических операций- способов выполнения действий. На данном уровне мы формируем алгоритмическую структуру математической деятельности.
Пример задания данного уровня: Исследовать ряд на сходимость: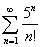 
следующим образом:
1) Выписать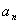 
;
2) Проверить необходимый признак сходимости, для этого найти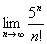 
;
3) Применить признак Даламбера, найти: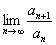 
;
4) Сделать вывод.
Решая такого типа задания, между изучаемыми объектами устанавливаются определенные связи и отношения, возникает качественно новое интегративное знание в сознании студента. Формирование данного уровня идет в теоретическом блоке краткого изложения, все примеры, подкрепляющие теоретические знания, следует решать в алгоритмическом виде.
Уровень распознавания: предполагает научить студентов распознавать усвоенное математическое понятие, обучить действиям классификации, сравнения и обобщения.
Пример заданий данного уровня:
1. Какое значение должно принять k в ряде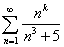
, чтобы, применяя необходимый признак сходимости, мы знали, что ряд: а) расходится; б) может сходиться.
2. Что следует написать вместо …. в ряде Фурье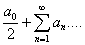
, для четных функций с периодом Т=2π:
а)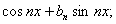 
б) 
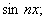в)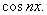 
Такого рода задания, нацеленные на формирование уровня распознавания, следует применять на первых занятиях блока применения, совершенствуя их переходить к последнему уровню.
Уровень систематизации знаний: высоким уровнем систематизации знаний является формирование научных теорий, представляющих собой целостную систему знаний. На данном уровне применяются упражнения на восстановление компонентов задания; на восстановление исходной части задания по результату; на выявление зависимости результата от изменения
условия задания. На основе нескольких типичных примеров предлагается выяснить закономерности их решения и вывести общие формулы либо правила их решения, а также задания, решение которых предполагает самостоятельный, неалгоритмический поиск решения.
Примеры заданий:
1. Проанализируйте и запишите, какие признаки сходимости и правила вычисления были применены для решения следующих задач:
а)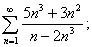 
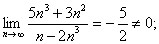ряд расходится.
б)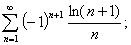 
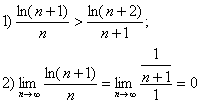ряд сходится.
в)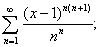 
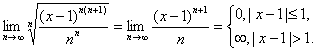ряд сходится на отрезке [0;2].
2. Составьте примеры рядов, сходимость или расходимость можно доказать используя а) признак Коши; б) признак Лейбница.
3. Найдите ошибки (предоставить студентам решенные задачи на исследования ряда с заведомо сделанными ошибками).
Работа по данным уровням должна выполняться по всем изучаемым темам, в результате чего получим прочную систему математических знаний.
Литература:
1. Буркина В. А., Титова Е. И. Механизмы систематизации знаний// Молодой ученый. 2014. № 3 (62). С. 884–886.
2. Ермолаева Е. И. Систематизация математических знаний студентов строительных специальностей в процессе реализации модульного обучения [Текст]: Дис.... канд. пед. наук: 13.00.08/ Е. И. Ермолаева — Пенза, 2008. — 170 с.
3. Ермолаева Е. И. Систематизация математических знаний у студентов строительных специальностей в рамках модульного обучения// Наука и школа. 2008. № 1. С. 33–37.
4. Ермолаева Е. И. Проблемы усвоения математических знаний студентами технических вузов// Актуальные проблемы гуманитарных и естественных наук, № 7, 2010г. С. 270–272.
5. Ермолаева Е. И. Изложение темы «Ряды» с учетом ее математической значимости// Известия Пензенского государственного педагогического университета им. В. Г. Белинского. 2010. № 22. С. 220–225.
6. Ермолаева Е. И., Куимова Е. И. О важности фундаментальной математической подготовки студентов по направлению «Строительство»// Известия Пензенского государственного педагогического университета им. В. Г. Белинского. 2011. № 26. С. 463–467.
