В статье рассматривается авторский метод анализа и математического моделирования неоднородных совокупностей на основе функции сходства многомерных объектов, а также на использовании многокритериального выбора по отношению Парето. Представлена его адаптация к описанию авторской научной концепции сбалансированного распределения инновационных ресурсов промышленного предприятия между объектами инноваций.
Ключевые слова: инновации, инновационные ресурсы, научная концепция сбалансированного распределения инновационных ресурсов промышленного предприятия между объектами инноваций, системный анализ эффективности.
Введение
В современных условиях, когда США и страны Европейского Союза вводят экономические санкции в отношении наиболее инновационно-активных российских промышленных предприятий, особую актуальность приобретает разработанная автором научная концепция сбалансированного распределения инновационных ресурсов предприятий между объектами инноваций, эндогенной основой которой являются инновационные самоорганизующиеся бизнесобразующие технологии. Суть данной концепции была нами подробно изложена в ранее опубликованных работах. [1]
Информационные и когнитивные технологии, наряду с технологиями информационных и управляющих систем, входят в перечень критических технологий современной России, определенный в Указе Президента России № 899 от 7 июля 2011 года, а также являются приоритетными направлениями развития науки, технологий и техники согласно «Прогнозу научно-технологического развития Российской Федерации на период до 2030 года».
В сферах разработки новых когнитивных технологий для эффективного и рационального управления инновационными ресурсами предприятий необходима обработка очень больших информационных массивов. Все это обусловливает необходимость широкого использования выборочного метода, основу которого составляет закон больших чисел. В существующей реальности любая генеральная совокупность является заведомо неоднородным множеством, структурированным по различным номинальным (классификационным) шкалам, а проблему неоднородности (структурированности) процесса сбалансированного распределения инновационных ресурсов между инновациями можно решить на основе одного из двух подходов:
- создав неслучайную выборку, репрезентативную изучаемой совокупности по многомерной структуре (хотя бы нескольким основным номинальным шкалам);
- математически корректно учесть при компьютерной обработке данных различия между структурами генеральной совокупности и выборочного объекта.
Более перспективным, на наш взгляд, является второй подход. Этот подход среди исследователей пока не нашел заметного развития, хотя, требуя значительного объема компьютерных расчетов, он и решает указанную задачу. В этой связи теоретически, методически и практически актуальной является проблема разработки и внедрения методов анализа и математического моделирования неоднородных совокупностей на основе функции сходства многомерных объектов, а также на использовании многокритериального выбора по отношению В.Парето.
Функция сходства многомерных объектов.
Под объектом мы будем понимать совокупность мероприятий по распределению инновационных ресурсов предприятия между инновациями, выраженное вектором признаков, измеряемых в числовых шкалах (в том числе — дихотомической). Пусть множество Х, состоит из элементов 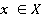 .
.
Любая классификация, в том числе и социально-экономическая, всегда
основана на анализе какой-либо меры близости [2] многомерных объектов. Функцию 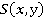 , заданную на декартовом произведении
, заданную на декартовом произведении 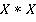 , вида
, вида 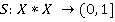 называют мерой близости элементов множества Х в том случае, если выполнены аксиомы:
называют мерой близости элементов множества Х в том случае, если выполнены аксиомы:
(а) условие нормировки:
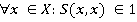 (1)
(1)
(мера близости S любого элемента х «к самому себе» равна 1);
(б) условие симметричности:
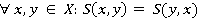 (2)
(2)
Для того чтобы мера близости (сходства, подобия), определенная на основе аксиом (1,2), стала «рабочей», нужно договориться о том, как измеряется расстояние между парами элементов Х,т. е.определить на Х некоторое метрическое пространство [3, гл. 3,4].
В связи со сказанным заметим, что в монографии Г. Г. Татаровой [4], посвященной вопросам социальной типологизации, сразу же после определения меры S(х,у) приведены некоторые часто используемые величины такого рода [4,с.213]. Но очевидно, что все они определены не просто для множества объектов Х, а на нормированных пространствах
[3, гл. 3], построенных на Х. Метрика ρ, определенная на множестве Х, представляетсобой отображение вида:
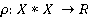
где R — множество неотрицательных чисел, при условии выполнения аксиом:
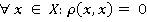 (3)
(3)
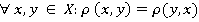 (4)
(4)
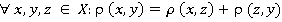 (5)
(5)
Легко понять, что аксиомы (3 и 4), являясь аналогами аксиом меры подобия (1,2), описывают «сходство» объектов «с противоположной позиции». Условие (5) («аксиома треугольника») — обобщение той «истины», что «прямая есть кратчайшее расстояние между двумя точками».
Определим функцию сходства объектов. Причем сделать это наиболее удобно в стохастическом смысле. Пусть нормированное пространство N определено на множестве объектов Х. Производится опыт, состоящий в том, что из множества X случайным образом выбирается его элемент x. Оказывается, что норма [3, п.3.3]x равна r(x).Врезультате серии из n таких опытов образуется статистика вида { r1, r2,..., rn }. Величина r в описанной серии опытов (по схеме Бернулли) ведет себя как стохастическая переменная и, следовательно, имеет некоторое распределение  .
.
Функцией распределения нормы (ф.р.н.)  элементов множества X,
элементов множества X,
на котором определено нормированное пространство N, назовем вероятность того события, что норма наугад выбранного элемента x 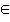 N окажется меньше r:
N окажется меньше r:
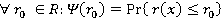
где: r(x) — норма случайно выбранного объекта x 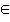 N
N
Pr { … } вероятность события { … }. Приведенное определение ф. р.н. является строгим,но опирается не на описание вероятности по А. Н. Колмогорову [5], а на описание вероятности по Мизесу — Смирнову — Виллю — Постникову [6].
Пусть на множестве Х определено нормированное пространство 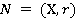 . Функцией сходства назовем отображение θ(х,у)такое,что
. Функцией сходства назовем отображение θ(х,у)такое,что
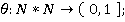 (7)
(7)
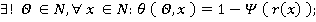 (8)
(8)
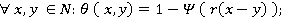 (9)
(9)
где 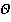 — начало координат, а величина r(x — y) является расстоянием между x и y в метрике,порождаемой нормой[3,гл.3].
— начало координат, а величина r(x — y) является расстоянием между x и y в метрике,порождаемой нормой[3,гл.3].
Пример.Пусть дано множество объектов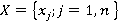 ,каждое из которых определено случайным вектором показателей вида:
,каждое из которых определено случайным вектором показателей вида:
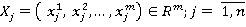
Будем считать, что все компоненты этого вектора имеют стандартизованное гауссово распределение g(0,1). В сферической евклидовой метрике расстояние между элементами 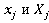 из Х имеет вид:
из Х имеет вид:
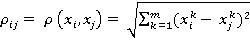 (10)
(10)
Из теории распределений известно, что случайная величина 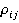 имеет функцию плотности вероятностей вида:
имеет функцию плотности вероятностей вида:
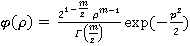 (11)
(11)
Тогда функция сходства любой пары объектов 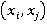 имеет вид
имеет вид
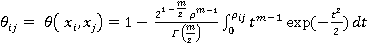 (12)
(12)
Таким образом: привлекательность функции сходства θ состоит в том, что типологическое пространство объективно описывает подобие объектов (процессов сбалансированного распределения инновационных ресурсов промышленных предприятий между объектами инноваций) всей генеральной совокупности.
Типологическим пространством,заданным на абстрактноммножестве объектов Х, называется пара 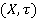 , где типология
, где типология 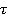 -система аксиом, задающих «правила» принадлежности границ всевозможных подмножеств Х. Итак, типологическое пространство является частным случаем нормированного пространства, нормированное — метрического, а метрическое — частным случаем типологического пространства.
-система аксиом, задающих «правила» принадлежности границ всевозможных подмножеств Х. Итак, типологическое пространство является частным случаем нормированного пространства, нормированное — метрического, а метрическое — частным случаем типологического пространства.
Отношение Парето как основа анализа уровня объектов.
Наряду с традиционными методами классификации (Q-техника факторного анализа, кластерный, дискриминантный, таксонный анализ и эвристическая типологизация) большую роль играют методы систематизации многомерных объектов поих уровню, которые относятся к методам многокритериальной оптимизации.
Нами предлагается метод анализа уровня объектов, основанный на использовании многокритериального выбора по отношению В. Парето. Заметим, что отношение Парето в прикладных задачах многокритериального выбора и ранее широко использовалось в научных исследованиях [7].
Для радикального повышения стабильности анализа уровня объектов по отношению Парето используем аппарат ранговых статистик.
Упорядочим значения показателей 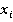 в вариационные ряды, для простоты изложения — без связок вида
в вариационные ряды, для простоты изложения — без связок вида 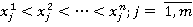 . Номер объекта
. Номер объекта 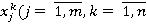 в вариационном ряду, называемый рангом этого объекта, обозначим
в вариационном ряду, называемый рангом этого объекта, обозначим 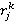 .
.
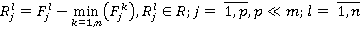 (13)
(13)
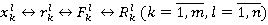
Поскольку все произведенные преобразования объективны, подобны, то результаты анализа уровня объектов 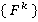 правомерно рассматривать как анализ уровня объектов
правомерно рассматривать как анализ уровня объектов 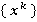 .
.
Проведем разбиение множества объектов 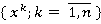 на классы мажорант Парето в пространстве
на классы мажорант Парето в пространстве 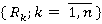 так, как это описано выше.
так, как это описано выше.
При этом совокупность классов мажорант Парето образует разбиение исходного множества генеральной совокупности всех возможных вариантов сбалансированного распределения инновационных ресурсов промышленных предприятий между объектами инноваций в условиях неопределенности на непересекающиеся подмножества сходных объектов:
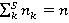 (14)
(14)
Заключение
Предлагаемая автором методика была апробирована на данных нескольких российских предприятий. В результате были выделены несколько групп моделей сбалансированного распределения инновационных ресурсов промышленных предприятий между различными объектами инноваций в условиях неопределенности. Это означает, что в каждую группу мажорант по отношению Парето попали математические модели и алгоритмы с примерно одинаковым уровнем баланса эффективности.
Таким образом: после экспертного анализа, подтвердившего экономическую состоятельность выявленной классификации математических моделей и алгоритмов оптимизации сбалансированного распределения инновационных ресурсов промышленных предприятий между различными объектами инноваций, отраженные в данной статье результаты могут быть использованы для подготовки объективно управляющих решений менеджеров различных звеньев для оптимизации инновационной активности российских предприятий в условиях нарастающей нестабильности во взаимоотношениях России со странами Евросоюза и США.
Литература:
1. Лавриченко О. В. Инновационные бизнесобразующие технологии как эндогенная основа инновационной системы промышленного предприятия: монография.- М.: Изд-во Московского гуманитарного университета,2014.-136 с.
2. Раушенбах Г. В. Меры близости и сходства. — М.: Наука,1986. — С.169–203.
3. Колмогоров А. Н.,Фомин С. В. Элементы теории функций и функционального анализа. — М.: Наука,1976. — 542 с.
4. Татарова Г. Г. Основы типологического анализа в социологических исследованиях. — М.: Высшее образование,2007. — 236 с.
5. Загоруйко Н. Г. Распознавание образов методом попарного сравнения эталонов // Доклады РАН. -2002.-Т.382.-№ 1.-С.1–3.
6. Постников А. Г. Арифметическое моделирование случайных процессов // Труды Матем.института АН СССР им.Стеклова.-1960.-Т.57.-С.272–291.
7. Айвазян С. А. Анализ качества и образа жизни населения.-М.:Наука,2012.-432 с.

