При построении теней на перспективных чертежах за источник света принимается солнце, которое по отношению к картине может занимать различные положения:
1. солнце расположено позади предмета и тень падает в сторону наблюдателя (рис.1);
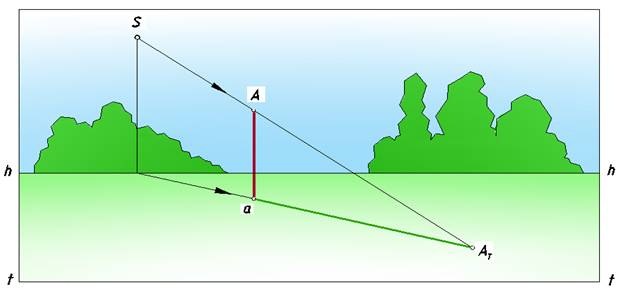
Рис. 1. Солнце позади предмета
2. солнце расположено позади зрителя, тень падает в сторону линии горизонта от основания предмета (рис. 2);
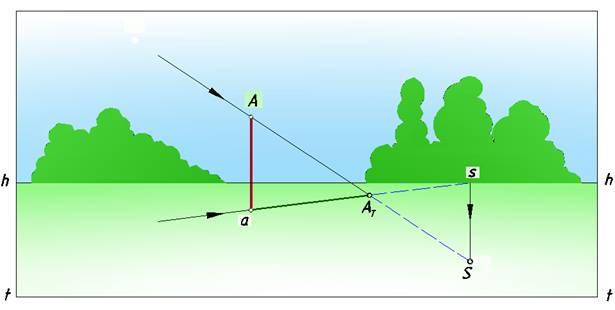
Рис. 2. Солнце позади зрителя
3. солнце расположено сбоку так, что лучи идут параллельно картине (рис. 3).
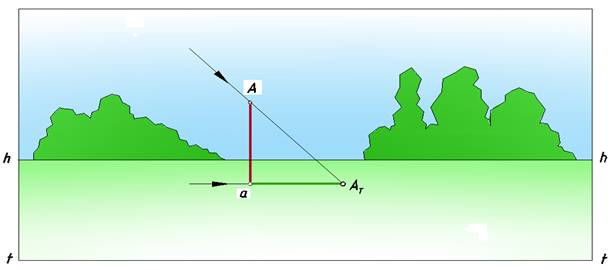
Рис. 3. Солнце сбоку предмета
Последний случай чаще других применяется инженерами при построении перспективных изображениях зданий и сооружений, поэтому остановимся на нем более подробно.
Рассмотрим построение точки в перспективе. Будем считать, что объект освещается слева (или справа), лучи идут параллельно картине, составляя угол 45° с предметной плоскостью. Запишем эти условия символически:
1. S∥K;
2. S^T= 45°.
Проведем через точку A (рис. 4) перспективу луча, а через ее вторичную проекцию (точку a) — вторичную проекцию луча. Поскольку луч параллелен картине, его вторичная проекция параллельна основанию картины t — t. Точка пересечения перспективы луча с его вторичной проекцией определит действительную тень точки А на земле — точку АТ.
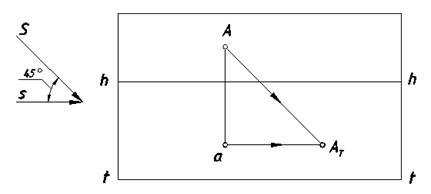
Рис. 4. Тень точки в перспективе
Построим собственные и падающие тени параллелепипеда, стоящего на земле (рис. 5).
Заметим, что те выводы, которые были сформулированы ранее для построения теней в ортогональных проекциях, справедливы и для центральных.
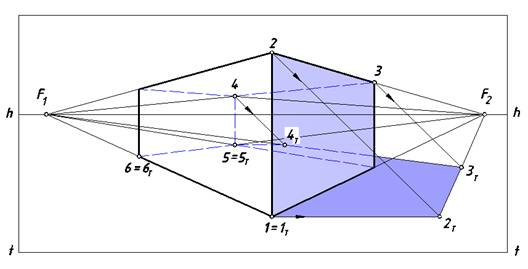
Рис. 5. Построение теней параллелепипеда
Проанализируем освещенность граней параллелепипеда. При заданном направлении лучевого потока освещенными будут верхняя, левая видимая и невидимая на чертеже грани объекта. Остальные грани окажутся в собственной тени. Определим контур собственной тени данного тела. В его состав войдут ребра (12) — (23) — (34) — (45) — (56) — (61), составляющие замкнутую цепочку в виде пространственной ломаной линии. От выявленного контура строим падающую тень. Поскольку точка 1 лежит на земле 1 = 1Т. Проведем через точку 2 перспективу луча, а через ее вторичную проекцию (точку 1) — его вторичную проекцию. На пересечении этих линий находим точку 2Т. Поскольку ребро [23] параллельно предметной плоскости, его падающая тень равна и параллельна ему. Точка схода ребра (23) находится на линии горизонта (точка F1). Соединяем точку 2Т с этой точкой (т. е. проводим через нее прямую, параллельную этому ребру). На этой же прямой находится тень точки 3. Проведем через точку 3 перспективу луча до пересечения с построенной прямой — определим точку 3Т. Вторичную проекцию луча в этом случае строить не следует, поскольку искомая точка уже установлена пересечением двух линий. Ребро (34) также параллельно плоскости T, его тень параллельна ребру.
Точкой схода этих прямых — фокус F1. Проведя перспективу луча через точку 4 до пересечения с отрезком (3Т F1), определим точку 4Т. Точки 5 и 6 расположены на предметной плоскости T, поэтому 5 = 5Т и 6 = 6Т. Очертание контура падающей тени параллелепипеда состоит из совокупности отрезков (1Т 2T) — (2Т 3T) — (3Т 4T) — (4Т 5T) — (5Т 6T) — (3Т 4T), представляющих собой замкнутый контур.
Задача
Построить тени от прямых барьеров на лестнице, земле и стене
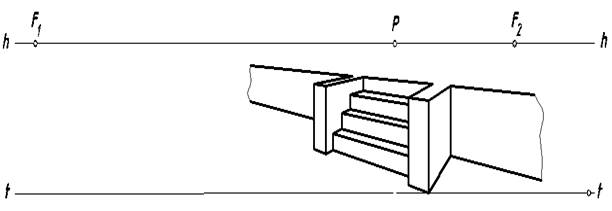
Рис. 6. Лестница с прямыми барьерами
Вначале построим тени правого барьера (рис.49). Поскольку при заданном направлении светового потока правая грань барьера находится в собственной тени легко видеть, что ребра, находящиеся на границе света и тени войдут в состав контура собственной тени. Определим падающую тень вертикального ребра. Точка А принадлежит Т, поэтомуможно отметить, что А = АТ. Проведем через точку В перспективу луча, а через ее вторичную проекцию — точку А перспективу вторичной проекции луча. На пересечении построенных линий определим тень ВТ.Другое ребро BC параллельно предметной плоскости, следовательно, его тень параллельна ребру и имеет ту же точку схода F2. Реальная часть этой тени на земле — отрезок ВТ1Т. Поскольку точка 1Т находится на границе земли и стены 1Т = 1Т'. С помощью обратного луча можно определить точку на ребре BC, которая отбросила эту тень. Точка С горизонтального ребра находится на стене, поэтому С = СТ'. Тень отрезка 1C падает на стену. Его тенью является отрезок 1Т' СТ'.
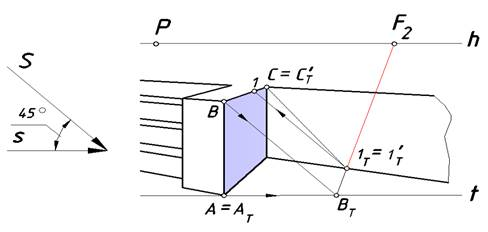
Рис.7. Построение контура падающей тени правого барьера
Контур собственной тени всегда замкнут. Рассуждения по его определению приводились во многих задачах. Элемент контура может совпадать со своей тенью (если, например, он находится на земле, стене или примыкает к другому объекту). Этот фактор следует учитывать при построении падающей тени.
У левого барьера правая грань находится в собственной тени, следовательно, ребра LN и LM входят в состав определяемого контура (рис. 8). Построим падающие тени этих ребер.
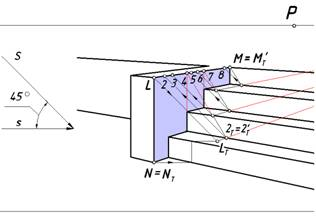
Рис.8. Построение контура падающей тени левого барьера
Лучевая плоскость (фронтальная плоскость уровня), проходящая через ребро LN пересекает землю и нижнюю ступеньку по параллельным прямым, оставляя на них теневые следы, а подступенок по вертикальной прямой. Верхняя точка L этого ребра отбрасывает тень на первую ступеньку и определяется пересечением луча с его вторичной проекцией. Ребро LM параллельно плоскости нижней ступеньки, поэтому его тень параллельна ребру. Соединяет точку LТсточкой схода F2иотмечаем реальную часть тени этого ребра на нижней ступеньке до точки 2Т = 2Т'. Заметим, что это ребро является гвоздем по отношению ко всем подступенкам. Проведем вспомогательные линии для нахождения общих точек для ребра LM и граней всех подступенков. Эти построения позволят определить падающие тени на подступенки. На рис. 8 на ребре LM отмечены все его участки, отбросившие тени на конкретные фрагменты лестницы, землю и стену.
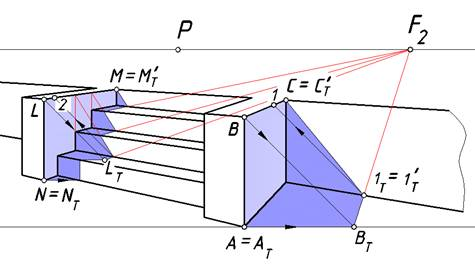
Рис. 9. Собственные и падающие тени от прямых барьеров
На рис. 9. представлен окончательный вариант решения задачи. Тени ребер LM и BC на стене и подступенках параллельны и представляют собой пример восходящих прямых. Их точка схода расположена выше линии горизонта, а точка схода их вторичных проекций лежит на линии горизонта.
Литература:
1. Макарова М. Н. Перспектива / М. Н. Макарова. — М.: Академический проект,2002.–512 с.
2. Яблонский А. Г. Начертательная геометрия (перспектива) / А. Г. Яблонский. — М.: из-во «Просвещение», 1966. — 176 с.

