Расчет динамики накопления и кристаллизации соли в выпарном аппарате с переменными параметрами в спускной циркуляционной трубе

Московский государственный технический университет имени Н.Э. Баумана

Предложена методика расчета динамики накопления солевого раствора в выпарном аппарате с выносной нагревательной камерой [1–3]. Данное устройство предназначено для повышения концентрации подаваемого исходного раствора соли. Рассмотрен аварийный режим с течью из спускной циркуляционной трубы выше нижней высотной отметки поверхности нагрева в нагревательной камере. Возникают динамические процессы изменения концентрации раствора соли, включая фазовые переходы — образования твердой фазы из насыщенного солевого раствора в нагревательной камере. В циркуляционную трубу производится подача раствора соли.

Расчетная область рассматривается в виде U-образного сосуда, в нисходящей ветви которой поддерживается постоянный уровень, а в восходящей ветви производится подвод тепла, кипение, повышение концентрации солевого раствора и кристаллизация.

Ключевые слова: плотность, расход, выпаривание, соль, растворитель, раствор, концентрация, жидкая фаза, твердая фаза, кристаллизация.

Введение. На простом примере — выпарном аппарате,- предложена методика расчета динамики изменения концентрации соли и кристаллизации. Во многих технических отраслях данные процессы являются актуальными.

Конструкция выпарного аппарата с выносной нагревательной камерой хорошо известна [1‑3]. Пусть в необогреваемой циркуляционной трубе возникла течь выше высотной отметки места подачи исходного раствора в циркуляционную трубу и выше нижней высотной отметки поверхности теплообмена в нагревательной камере. После разгерметизации все процессы будем рассматривать при неизменном значении давления — p(τ)=const, где p — давление, Па. Для упрощения пусть температура жидкой и твердой фазы остается неизменной и равна T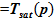, гдеT — температура в градусах Кельвина, К. Поиск зависимостей для параметров, описывающих динамические процессы в выпарном аппарате, является объектом исследования. Использована точечная модель с сосредоточенными параметрами. Уравнение состояния для компонентов среды известно: плотность растворителя (нижний индекс — _sv) — 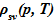, кг/м³,плотность кристаллов соли (нижний индекс — _cr) — 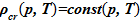[4], зависимость плотности раствора от концентрациизадана следующим образом — 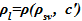,  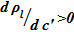(плотность раствора с ростом концентрации увеличивается [4, 5]), известна предельная концентрация раствора соли при заданной температуре — 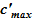(T), (здесь c’- концентрация г соли/1 кг раствора).

Модель двухфазной смеси (сосуществование жидкой и твердой фаз) следующая. Жидкая фаза является раствором соли предельной концентрации c’=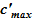, а образование твердой фазы постулируется только лишь на стенках сосуда. В результате при записи закона Паскаля для двухфазной смеси используется плотность раствора жидкости, соответствующая предельной концентрации .

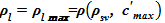Плотность двухфазной смеси 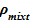, используемая для вычисления массы в известном объеме, равна 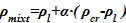, где α= 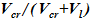— объемное содержание твердой фазы (где V — объем, м³). Удельный объем (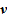) двухфазной смеси определяется при известных удельных объемах жидкой и твердой фаз с использованием массового содержания твердой — χ=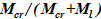, — фазы  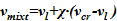(где M — масса, кг).

Отдельные слагаемые разработанного алгоритма были опубликованы авторским коллективом ранее [6–8]. Но рассматривались упрощенные граничные условия, которым очень трудно найти обоснование в технических отраслях. Это строго фиксированные уровни и параметры раствора в опускном участке; подвод жидкости с переменными параметрами извне исключительно в подъемный участок; равенство между подводом жидкости извне и расходом образующегося пара и т. д.

Постановка задачи. Схема расчетной области представлена на рисунке 1. Имеется расчетная область, которая представляет собой два сообщающихся сосуда-объема, т. е. опускной участок — down volume (верхний индекс для параметров в ней — ^dn) и подъемный участок — upper volume (верхний индекс для параметров в ней — ^up). Зависимость площади поперечного сечения 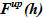 и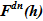, м² для обеих подобластей от высотной отметки известны. Последнее позволяет определять соответствующие объемы (нижняя высотная отметка постоянна, верхняя высотная отметка уровня жидкости в опускном участке является «плавающей», ограничена местом течи 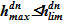, м и балансом расходов): 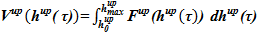, где V — объем, м³, h — высота, м, τ — время, с) и 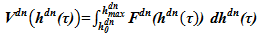. Масса среды, заполняющего верхний и нижний объемы, может определяться следующим образом —  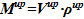и 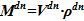. Еще раз следует напомнить: 1) двухфазная смесь может существовать лишь в подъёмном участке; 2) в опускном участке постулируется пребывание раствора соли с переменной концентрацией и изменяющимся уровнем.

В опускной участок осуществляется подача жидкости из ряда источников — i=1, n. Временные зависимости расходов растворов соли 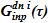 а также их концентрации 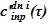, известны из граничных условий. Для упрощения изложения постулируется, что температура подаваемого раствора равна температуре насыщения, соответствующей давлению окружающей среды — 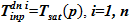.Подача недогретой до температуры насыщения жидкости приведет к появлению еще одного параметра, не повлияв на суть самой методики. Учет тепловых балансовых соотношений в данных аппаратах ранее подробно изложен [1‑3].

В опускном участке существует переток жидкого раствора соли 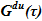 с концентрацией, равной текущему значению в down volume — 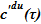. Значение данного расхода является искомым параметром процесса. Кроме того, по достижении максимального уровня в опускном участке и превышении притока над оттоком  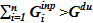возникает нестационарный перелив раствора соли  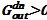с переменной концентрацией в течь. Концентрация раствора соли в  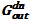определяется, в первую очередь, из слагаемых 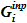сминимальной концентрацией 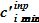. Объяснение — плотность для растворов большинства солей [4] с минимальной концентрацией является наименьшей, а также — достижение консервативности оценки для результата расчета. Таким образом, параметр  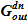также является искомым параметром моделируемого процесса.

В подъемном участке — upper volume — производится подвод тепла, зависимость мощности от времени — N(τ), Вт — известна из граничных условий –N(τ)=f₁(τ). В связи с тем, что температура раствора соответствует температуре насыщения, то все подведенное тепло расходуется на испарение растворителя. Расход образующегося пара определяется соотношением 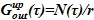, где теплота парообразования r, Дж/кгзадана r=i”(T_sat) — i’(T_sat), здесь i”(i’) — энтальпия пара (жидкости) при температуре насыщения T_sat(p), Дж/кг. Содержанием соли в образующемся паре с целью повышения консервативности оценки пренебрегаем, т. е. .

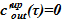Так как подъемный и опускной участки представляют собой сообщающиеся сосуды, то справедлив закон Паскаля 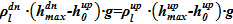, где 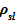 — плотность раствора соли, g — ускорение свободного падения, м/с².

Начальные условия. Вначальный момент времени τ=0 сообщающиеся сосуды заполнены до максимального уровня 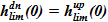 (сечение течи) раствором соли с концентрацией 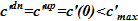, соответственно, плотности раствора 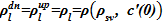. В соответствии с законом Паскаля, уровни в обоих сосудах одинаковы.

Граничные условия. Известны зависимости от времени для источниковых членов в опускном участке — 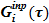, i=1, n и соответствующие концентрации подаваемых растворов соли 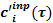, i=1, n. Известна зависимость от времени подведенной в подъемном участке мощности, используемой на парообразование — 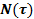, с помощью которой определяем расход образующейся паровой фазы .

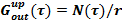Основные уравнения. Основной состав используемых зависимостей был перечислен выше. Для поиска параметров в подъемном участке используются следующее:

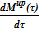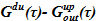 =  — масса среды;

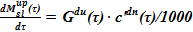 — суммарная масса соли (в жидкой и твердой фазе);

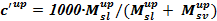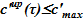 для , — случай существования только жидкой фазы, раствора соли;

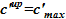 — случай двухфазной смеси, когда имеется жидкая и твердая фаза;

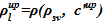 — зависимость плотности раствора соли от концентрации;

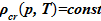 — плотность твердой фазы — кристаллов,- задана, неизменна.

Основные зависимости для параметров в опускном участке:

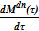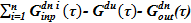 =  — масса среды — жидкого раствора;

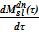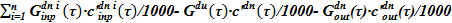 =  — масса соли в растворе;

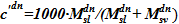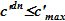 для , — случай существования только жидкой фазы, раствора соли. В рассматриваемой задаче всегда;

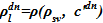 — зависимость плотности раствора соли от концентрации;

Алгоритм поиска решения проще представить в виде двух последовательных этапов. Первый процесс — однофазное выпаривание растворителя, накопление массы соли, рост концентрации раствора, что происходит вплоть до достижения предельной концентрации. При этом увеличивается плотность раствора, что оказывает, в соответствии с законом Паскаля, влияние на уровень раствора соли в подъемном участке. Это приводит к снижению объема, занятого раствором соли в подъемном участке. Первый этап — процесс однофазного выпаривания растворителя,- заканчивается достижением предельной концентрации раствора соли; далее наступает второй этап — выпаривание растворителя из двухфазной смеси. На протяжении второго этапа процесса приток соли, содержащейся в расходе 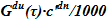, приводит к дальнейшему накоплению твердой фазы — кристаллов. Плотность раствора соли, участвующая в записи закона Паскаля, остается неизменной и соответствует предельной концентрации. В зависимости от этапа расчета в значительной мере изменяются расчетные параметры и связь между ними, что подробно отражено в записи методики расчета.

Методика расчета однофазного выпаривания растворителя.

Интегрирование производится с помощью численного метода Эйлера, поиск решения — параметров для следующего временного шага интегрирования,- выполняется методом деления отрезка пополам. Параметры с предыдущего временного шага при этом известны.

Поиск параметров для следующего временного шага 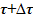 производится следующим образом.

Этап А. Параметры в опускном участке на этом этапе принимаем неизменными, «замороженными», для момента времени — τ. Производим поиск параметров для подъемного участка, применяем метод деления отрезка пополам.

1)        Вычисление 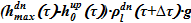 записи закона Паскаля для опускного участка с предыдущего временного шага;

2) 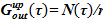        — расход пара, покидающего подъемный участок в результате парообразования;

3) 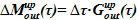        — масса пара, покидающего подъемный участок в результате парообразования

4)        Назначаем значение верхней и нижней границ поиска решения для массы раствора соли, поступающей из опускного участка 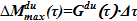 и .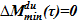

5) 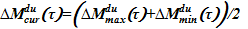       - задаем текущее значение для притока раствора соли из опускного участка

6) 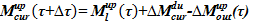       – масса раствора соли в подъемном участке

7) 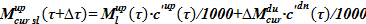        — масса соли в растворе

8) 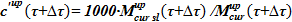        — новое значение концентрации раствора

9) 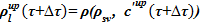        — новое значение плотности раствора соли

10) 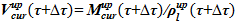    — объем раствора в подъемном участке

11) 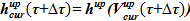    — использование геометрических данных для поиска текущего положения уровня раствора в подъемном участке

12)    Вычисление 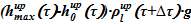 записи закона Паскаля для подъемного участка

13)    Сравнение весовых столбов в опускном и подъемном участке: если весовой столб в опускном участке (позиция А.1 алгоритма) превышает аналогичную величину для подъемного участка (позиция А.12 алгоритма), то 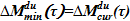, в противном случае — .

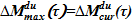14)    Производится повторение вычислений, начиная с позиции 5 алгоритма с учетом обновленных значений для поступлений раствора соли из опускного участка. Авторами были проведены тестовые расчеты, в которых получено достаточное значение итераций — n=10‑20, — для достижения удовлетворительных результатов.

15)    После поиска решения производится проверка физической достоверности результата — 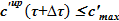. В противном случае — для поиска параметров процесса в подъемном участке следует использовать алгоритм поиска решения в двухфазной области. Он будет приведен далее и именуется «Этап В».

Этап Б. Параметры в подъемном участке на этой стадии принимаем неизменными, «замороженными». Запись искомого значения массы раствора в опускном участке:

,

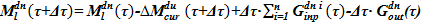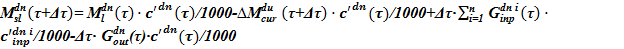 — масса соли в растворе в опускном участке.

При записи искомого значения следует учесть следующее:

-          отток раствора соли содержится в двух членах уравнения: 1. обязательный -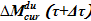; 2. «возможный» член — ;

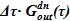-          подача раствора соли 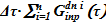 обеспечивают: 1. компенсацию оттока в подъемный участок 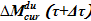; 2. возможный компонент, «дозаполнение» объема раствора в опускном участке при 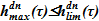; 3. «перелив» через сечение течи, т. к. максимальный уровень  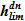и соответствующий объем  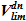задан в геометрическом описании расчётной области.

Последовательность следующая:

1) 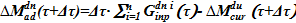        — определение возможности компенсации перетока из опускного участка в подъемный подаваемой раствором соли из внешних источников.

2)        Избыток жидкости может расходоваться на следующий пункт, если эта проблема существует — 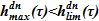.Определяем требуемые величины для заполнения опускного участка до высотной отметки места течи -: 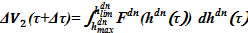, 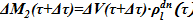. В обратном случае, когда 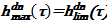, то .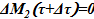

3)        Вычисляем 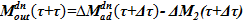. Если 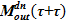>0, то для консервативности модели следует отбирать слагаемые 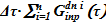, которые формируют  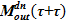следующим образом. Градация слагаемых  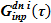определяется на основе 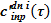: в опускном участке должна оставаться раствор соли из источников с максимальной концентрацией, а раствор соли из источников с минимальной концентрацией используется уходит в «перелив» — .

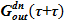4)        Определяем массу растворенной соли в опускном участке 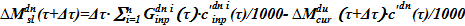 и концентрацию .

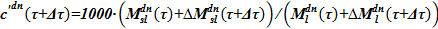5) 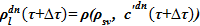        — новое значение плотности раствора соли

6) 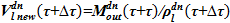        — осуществляем проверку и, в случае необходимости, корректировку слагаемых в записи  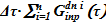этап Б пункт 3.

Еще раз напомним мотивацию пункта 3 для Этапа Б. При увеличении концентрации раствора соли увеличивается его плотность. Исходя из этого, а также для получения консервативной оценки объясняются манипуляции по выбору направления использования расходов 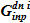 — на пополнение объема опускного участка расходуется «наиболее тяжелая жидкость» — раствор с максимальной концентрацией, «легкая жидкость» — поступающий извне раствор с минимальной концентрацией направляет наружу — в перелив .

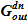Выше приведены алгоритмы поиска параметров для подъемного участка, случай однофазного существования раствора соли (Этап А), и опускного участка (Этап Б)

Этап Б. Вычисления производятся при наличии двухфазной смеси в подъемном участке для момента времени 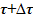 либо в случае достижения в этапе А концентраций, превышающих предельные значения .

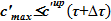1) 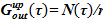        — расход пара, покидающего подъемный участок в результате парообразования

2) 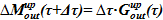        — масса пара, покидающего подъемный участок в результате парообразования

3)        Исходя из равенства 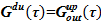, определяем компоненты массы соли и растворителя в подъемном участке следующим образом ,

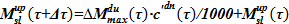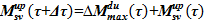
4) 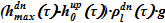        — запись закона Паскаля для опускного участка

5)        Из записи закона Паскаля для подъемного участка 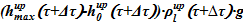 и известной величины в опускном участке можно вычислить соответствующее значение для 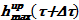. В этом случае 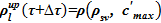, т. е. плотность жидкости для предельной концентрации соли.

6) 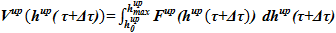        — определяем объем, занятый двухфазной смесью в подъемном участке.

7) 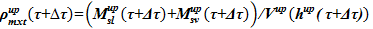       - плотность двухфазной смеси в подъемном участке

8) 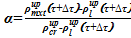        — определяем объемное содержание твердой фазы в смеси в подъемном участке

9) 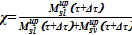        — определение массового содержание твердой фазы в смеси в подъемном участке

Предложенный алгоритм разработан для случая «накопления» соли в подъемном участке, т. к. истекающий расход 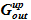 не содержит соли, а входящий расход — 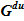,- является раствором соли. Изменение же граничных условий — появление концентрации раствора соли  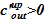в члене 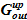,- может приводить к снижению концентрации и массы твердой фазы в подъемном участке. В этом случае алгоритм расчета должен быть изменен, что будет рассмотрено в дальнейшем.

Для иллюстрации работоспособности методики и воплощения алгоритма в программном средстве приведем некоторые расчетные результаты, полученные для раствора и кристаллов одной из солей — Рисунки 2‑5. Масштаб времени — ось абсцисс, — на всех рисунках одинаков, т. е. качественную динамику всех основных параметров процесса, включая связь между ними, можно проследить.

Заключение. Полученное знание — разработанная методика и программное обеспечение, — может с успехом применяться для решения различных задач науки и техники, если прослеживается идентичность схемы расчетного объекта с Рисунком 1 и происходят аналогичные физико-химические процессы.

Подробный анализ динамики накопления солей, включая образование твердой фазы, авторы планируют произвести в ходе дальнейшей работы.

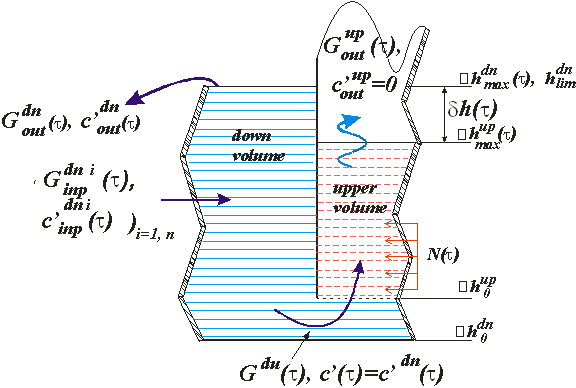
Рис. 1. Схема расчетной области

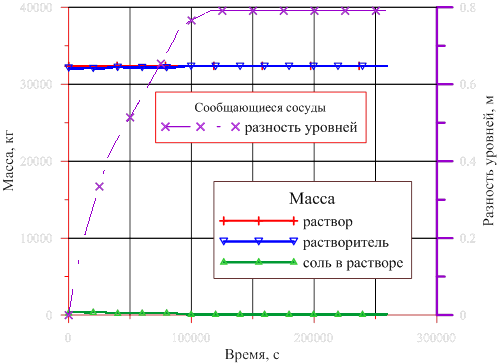
Рис. 2. Динамика составляющих массы в опускном участке рабочей области

Изменение разности уровней в сообщающихся сосудах

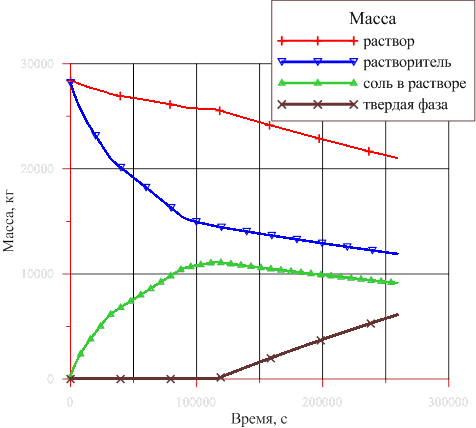
Рис. 3. Динамика составляющих массы в подъемном участке рабочей области

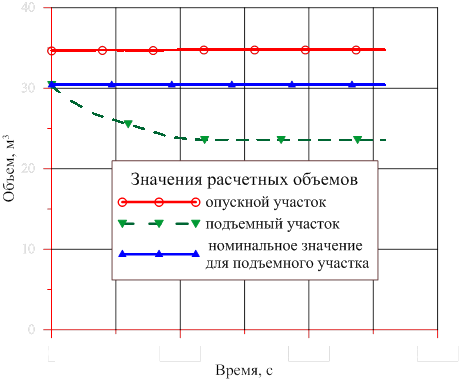
Рис. 4. Динамика изменения объемов, заполненных раствором и двухфазной смесью

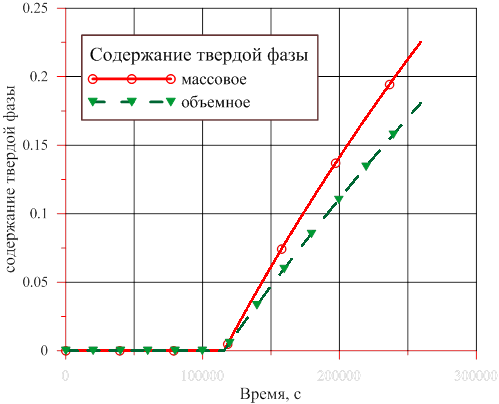
Рис. 5. Динамика изменения содержания твердой фазы в подъемном участке

Литература:

1.         Касаткин А. Г. Основные процессы и аппараты химической технологии. М.: Химия, 1971, 784 с.

2.         Гельперин Н. И. Основные процессы и аппараты химической технологии. М.: Химия, 1981, 812 с.

3.         Химическая энциклопедия. В 5 т.: Т. 1. Редакционная коллегия Кнуньянц И. Л. (гл. редактор) и др. — М., Советская энциклопедия, 1988, 623 с.

4.         Справочник химика. В 5 т.: Т. 2. Редакционная коллегия Никольский Б. П. (гл. редактор) и др. — Л., Ленинградское отделение Госхимиздата, 1963, 1168 с.

5.         Справочник химика. В 5 т.: Т. 4. Справочник химика. В 5 т.: Т. 3. Редакционная коллегия Никольский Б. П. (гл. редактор) и др. — М., Химия: 1965, 1168 с.

6.         Шмаль И. И. Аналитические оценки для процесса кристаллизации // Молодой ученый. — 2013. — № 7 (54), с. 30–31.

7.         Шмаль И. И. Метод расчета нестационарных изменений концентрации в выпарных установках // Молодой ученый. — 2013. — № 8 (55), с. 42–44.

8.         Шмаль И. И. Проблемы моделирования кристаллизации // Молодой ученый. — 2013. — № 8 (55), с. 44–47.