Оптимизация естественной освещенности помещений

Я хотел бы выразить искреннюю признательность Министерству высшего образования и научных исследований Ирака, предоставившему мне стипендию в дополнение к финансовой и моральной поддержке и позволившему мне провести свои научные исследования.

В этой статье приводятся необходимые сведения из области фотометрии и теории световых полей, которые необходимы для постановки основной задачи диссертации. Рассмотрены световые единицы, в которых измеряется освещенность, сила света и другие характеристики световых полей. Обсуждается понятие коэффициента естественной освещенности. Для формулировки задачи описаны способы математического моделирования полей естественной освещенности. Приводится также точная постановка задачи и анализируются возможные подходы к ее решению. Одним из методов оптимизации являются генетические алгоритмы. Ниже кратко рассмотрен математический аппарат этих алгоритмов, а также обсуждается возможности их применения к решению нашей задачи.

Свет — в физической оптике электромагнитное излучение, воспринимаемое человеческим глазом. В качестве коротковолновой границы спектрального диапазона, занимаемого светом, принят участок с длинами волн в вакууме 380–400 нм (750–790 ТГц), а в качестве длинноволновой границы — участок 760–780 нм (385–395 ТГц).

В широком смысле, используемом вне физической оптики, светом часто называют любое оптическое излучение, то есть такие электромагнитные волны, длины которых лежат в диапазоне с приблизительными границами от единиц нанометров до десятых долей миллиметра. В этом случае в понятие «свет» помимо видимого излучения включаются как инфракрасное, так и ультрафиолетовое излучения.

Коэффициент естественной освещённости — отношение естественной освещённости, создаваемой в некоторой точке заданной плоскости внутри помещения светом неба (непосредственным или после отражений), к одновременному значению наружной горизонтальной освещённости, создаваемой светом полностью открытого небосвода; выражается в процентах.

Формула:

,

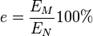где  — коэффициент естественной освещённости, 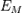 — естественная освещённость в точке  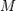внутри помещения, а  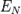— наружная освещённость на горизонтальной поверхности.

С помощью этого коэффициента производится нормирование естественного и совмещенного освещения в помещениях, коэффициент применяется при проектировании зданий и сооружений.

Модель естественной освещенности помещения

Световое поле, порожденное светопроемами в стенах и потолке помещения, можно описать безразмерным векторным полем. Это поле можно представить в безкоординатной форме следующим образом. Рассмотрим световой вектор равнояркой элементарной плоской поверхности площади DS, центр которой находится в точке M. Выпишем световой вектор в точке M₁ помещения. Если обозначить через 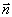(M) единичный вектор нормали к испускающей поверхности в точке M, направленный в сторону испускания, то указанный световой вектор запишется в виде

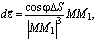                                                                                                               (1)

где j-угол между векторам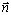и (M) и 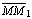. Для произвольной равнояркой испускающей поверхности, состоящей из элементарных площадок, получаем выражение для светового вектора в виде поверхностного интеграла по испускающей поверхности s:

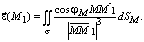                                                                                                   (2)

Обозначим через s₁-воспринимающую поверхность внутри помещения, а через 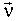(M₁)-единичный вектор нормали к поверхности s₁ в точке M₁, направленный в направлении светового потока. Тогда поток светового вектора через воспринимающую поверхность можно выразить формулой

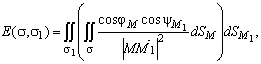                                                                      (3)

где 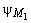-угол между векторами 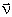(M₁) и 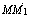. Величина E(s, s₁) является вещественно-значной функцией двух поверхностей s и s₁.

Отметим одно важное свойство изложенной модели потока светового вектора, которое можно назвать свойством симметрии. Если считать воспринимающую поверхность равнояркой светящейся поверхностью, а бывшую испускающую поверхность-воспринимающей, то поток светового вектора через последнюю будет равен величине E(s, s₁), определенной формулой (3), то есть справедливо равенство E(s, s₁)=E(s₁, s). Действительно, замена s®s₁ равносильна изменению направлений векторов 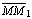, 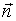(M), 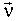(M₁) на противоположные. При этом величины cosj_M и cosy_M1 не изменятся. Само свойство симметрии является следствием возможности изменения порядка интегрирования.

Постановка оптимизационной задачи

Обычно в помещении можно указать поверхность (возможно состоящую из ряда связных частей), которая чаще всего нуждается в освещении. Эту поверхность мы в дальнейшем называем рабочей поверхностью. Естественно организовать естественное освещение этой поверхности так, чтобы поток светового вектора через нее был в некотором смысле наибольшим. Возникает задача оптимального использования площади светопроемов, то есть формы и места расположения светопроемов данной площади, которые обеспечивают наибольший поток светового вектора через заданную рабочую поверхность.

Для точной постановки задачи обозначим через W множество точек, расположенных на потолке и стенах помещения, в котором возможно расположение светопроемов различной формы. Множество W будем называть областью выбора. Эти светопроемы s являются измеримыми подмножествами точек, лежащих в W. Площадь светопроема или светопроемов s (если s не будет связным) обозначим через S(s). Обсуждаемую задачу можно сформулировать, как задачу на максимум функции области (множества) s:

E(s, s₁)®max,

при фиксированной поверхности s₁ и переменной области s Ì W, такой, что S(s)=S₀.

Алгоритм решения оптимизационной задачи

Дадим краткое описание простейшего алгоритма решения поставленной задачи.

Разобьем область W на элементарные площадки DW_i. Из этих площадок будем составлять оптомальную область s. Следует отметить, что для любой области s справедливы следующие равенства

E(s, s₁)=,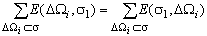

которые вытекают из аддитивности интеграла и свойства симметрии. Для каждой площадки DW_iÌW вычислим величину E(s₁,DW_i). Упорядочим все частичные площадки по значению этой величины, перенумеровав их в порядке ее убывания. Будем включать в s элементарные площадки в порядке убывания E(s₁,DW_i) до тех пор, пока справедливо неравенство S(ÈDW_i)≤S₀. Очевидно, что построенная так область s будет доставлять максимальное значение для E(s,s₁) среди всех областей, составленных из элементарных площадок DW_i.

Опишем подробно описанный выше алгоритм. Множество выбора W разобьем наmравных частей. Площадь каждой части обозначим через DS. Рабочая поверхность представляется в виде m₁ равных плоских частей, площадь каждой из которых обозначим через DS¢. В качестве входных данных возьмем два шестимерных массива

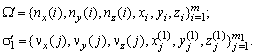
В каждом элементе массива 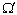 первые три координаты  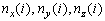являются координатами единичного вектора нормали в центре частичной площадки, на которые разбито множество выбора W, а 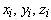-координаты этого центра. В каждом элементе массива  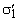первые три координаты  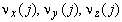суть координаты вектора нормали к рабочей поверхности в центре частичной площадки с номеромj, а 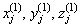-координаты этого центра. При этом вектор 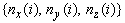направлен во внешность помещения, а вектор 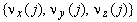-в направлении освещаемой стороны рабочей поверхности s₁. По разбиению поверхностей на части, заменяя интегралы интегральными суммами можно получить аппроксимацию величины E(s₁,DW_i), которую мы обозначим E_i(s₁). Для ее вычисления удобно использовать вектор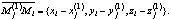

Далее можно написать

,

,

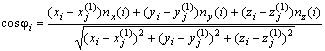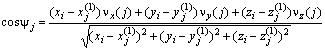E_i(s₁)=.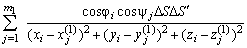

Отметим, что cosy_j может оказаться отрицательным. В дальнейшем удобно ввести величину

g_j=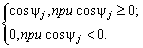

Каждой частичной площадке DW_i сопоставим ее оценку E_i относительно данной рабочей поверхности по формуле

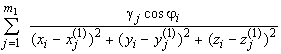E_i =.     (I)

Для каждой частичной площадки области выбора W вычислим величину оценки E_i и упорядочим площадки в порядке убывания этих оценок. Построим светопроемную область, состоящую из первых N частичных площадок, где натуральное число N выбрано из условия NDS=S₀ [1,2,3].

Вычисления можно представить в виде следующей укрупненной блок-схемы

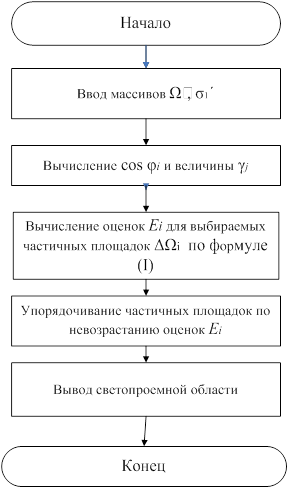
Основной задачей является определение таких светопроемов заданной площади производственных и других видов помещений, которые обеспечивают наибольшую среднюю освещенность рабочей поверхности, заданной внутри помещения. При этом отраженный свет не учитывается. Искомый светопроем состоит из элементарных площадок, выбираемых в некотором допустимом множестве точек на стенах и потолке помещения [4].

Литература:

1.                 Брусенцев А. Г., Гордица Д. Д. К расчету геометрического коэффициента естественной освещенности от зенитного светопроема прямоугольной формы // «Исследование строительных конструкций и сооружений», сб. трудов МИСИ — БТИСМ (1980), с.136–140.

2.                 Брусенцев А. Г., Гордица Д. Д. Повышение эффективности зенитных светопроемов // «Исследование строительных конструкций и сооружений», сб. трудов МИСИ — БТИСМ (1981), с. 126–131.

3.                 Брусенцев А. Г., Гордица Д. Д. Расчет оптимальной формы, площади и места расположения зенитных светопроемов одноэтажных производственных зданий // «Физико-математические методы в исследовании свойств строительных материалов и в их производстве». Сб. трудов МИСИ — БТИСМ (1982), с.184–189.

4.                 Мешков В. В. Основы светотехники: Учебное пособие для вузов. Ч. 1