Вработе рассматривается аксионные процессы в поле монохроматической циркулярно-поляризованной электромагнитной волны. Получены общие выражения для амплитуды и вероятности процесса, а также число переходов g -> a в единицу времени в единице объема. Выражение для вероятности процесса исследовано как в пределе «сильного», так и пределе «слабого» внешнего поля волны. Показано, что данный переход может иметь в обоих случаях резонансный характер. Результаты обладают достаточной степенью общности и могут быть использованы для получения ограничений на параметры аксиона, а также в астрофизике и космологии.
Ключевые слова: аксион, нейтрино, амплитуда распада, вероятность распада, элементарные частицы.
Введение.
Одной из центральных проблем современной физики является теория взаимодействия частиц и полей, в частности, теоретическое исследование моделей электрослабого взаимодействия, взаимодействие частиц с электромагнитным полем, которое может оказывать существенное влияние на процессы распада частиц (см. например [1–7]). Особое внимание уделяется простейшим моделям великого объединения с нестандартным набором хиггсовских частиц, легким и даже строго безмассовым хиггсовским частицам — голдстоуновским и псевдо-голдстоуновским бозонам. Хорошо известна проблема СР сохранения в сильном взаимодействии и естественное решение этой проблемы путем введения псевдоголдстоуновской частицы — аксиона.
Аксион — псевдоголдстоуновский бозон, призванный решить проблему нарушения СР — четности в стандартной модели. Он возникает при спонтанном нарушении глобальной симметрии U(1)pq, введенной в [8,9]. Взаимодействие аксионов а с фермионами f описывается лагранжианом (в естественной системе единиц ħ = с = 1)
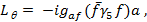
где 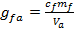 — безразмерная константа связи, mf — масса фермиона,
— безразмерная константа связи, mf — масса фермиона,
сf — численный коэффициент, зависящий от выбора конкретной модели, Va — энергитический масштаб нарушения PQ — симметрии.
Ввиду малости константы связи gaf (~ 1/Va) аксионные эффекты могут быть наиболее заметными в астрофизических условиях для которых характеры большие плотности вещества, высокие температуры, а также (в нейтронных звездах) сильные внешние электромагнитные поля.
1. Амплитуда перехода фотон ® аксион в поле плоской монохроматической волны.
Однопетлевой индуцированый внешним полем вклад в амплитуду перехода фотон ® аксион описывается диаграммой Фейнмана, изображенной на Рис. 1, где двойные линии означают, что в пропагаторах виртуальных фермионов влияние внешнего электромагнитного поля учтено точно. По виртуальным фермионам f в петле производится суммирование (f = q, l, где q — кварки. l — заряженные лептоны).
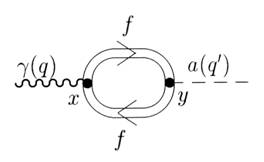
Рис. 1: Диаграмма Фейнмана, описывающая переход фотон-аксион во внешнем магнитном поле
Согласно диаграммной технике Фейнмана в низшем неисчезающем порядке теории возмущений выражение для S-матричного элемента во внешнем поле имеет вид:
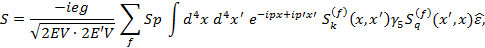
где e < 0, em — 4-вектор поляризации фотона. Для пропагатора заряженного фермиона 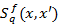 использовано точное решение волнового уравнения Дирака в поле монохроматической циркулярно-поляризованной волны.
использовано точное решение волнового уравнения Дирака в поле монохроматической циркулярно-поляризованной волны.
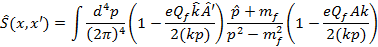
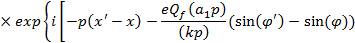
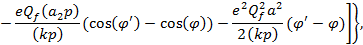
где, 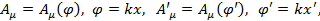 k — волновой 4-вектор
k — волновой 4-вектор
(k2 = 0), Qf и mf — относительный заряд и масса фермиона соответственно.
Выражение для S-матричного элемента может быть преобразовано к виду:
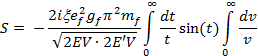
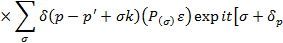
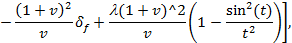
где
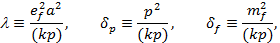
x = +1, -1 — описывает правую (левую) круговую поляризацию волны.
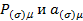 определены соотношениями
определены соотношениями
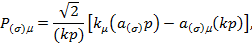
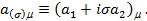
S-матричный элемент выражается через амплитуду М(s) следующим образом:
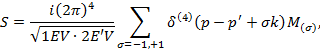 (1)
(1)
где рm и рm' — 4-импульсы начальной и конечной частицы.
Закон сохранения р' = р + sk однозначно фиксирует кинематику процесса:
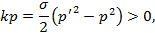
где параметр s = -1, +1 имеет смысл разности между числом поглощенных и испущенных фотонов внешней волны. Сам факт возможности существования только двух значений s является нетривиальным и связан не только с особенностью циркулярно-поляризованной волны, но и с типом конкретного распада.
Входящая в (1) инвариантная амплитуда М(s) может быть представлена в следующем виде:
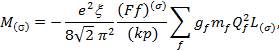 (2)
(2)
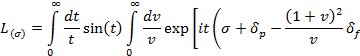 (3)
(3)
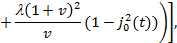
где j0(t) = sin(t)/t — сферическая функция Бесселя,
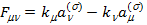 -тензор напряженности внешнего поля,
-тензор напряженности внешнего поля,
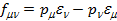 — тензор напряженности Фурье-образа поля фотона.
— тензор напряженности Фурье-образа поля фотона.
2. Переход фотон-аксион в поле монохроматической циркулярно-поляризованной волны.
Для этого процесса, s = +1, dр = 0, 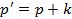 , 2(kp) = ma2, где ma — масса аксиона. Резонансное условие на энергию начального фотона:
, 2(kp) = ma2, где ma — масса аксиона. Резонансное условие на энергию начального фотона:
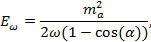
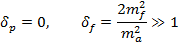 (4)
(4)
где ma << 1 MeV. В связи с условием (4) выражение для инвариантной амплитуды процесса резко упрощается:
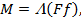 (5)
(5)
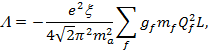
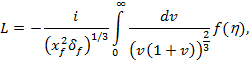 (6)
(6)
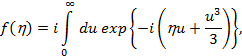
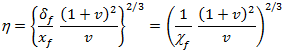
Заметим, чтоLв выражении (6) является интегралом от известной функции Харди-Стокса f(h).
Квадрат матричного элемента (5) после интегрирования по фазовому объему аксиона определяет вероятность исследуемого перехода в единицу времени:
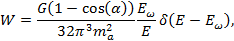 (7)
(7)
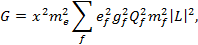
где 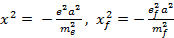 — параметр, характеризующий интенсивность волны. Ожидаемое число переходов в единицу времени в единице объема получается усреднением (7) по спектру начальных фотонов f(E):
— параметр, характеризующий интенсивность волны. Ожидаемое число переходов в единицу времени в единице объема получается усреднением (7) по спектру начальных фотонов f(E):
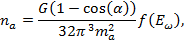
где a — угол между скоростью начального фотона и волновым вектором k.
3. Предел «слабого» поля.
Анализ функций L(s) (3), входящих в выражение для амплитуды М(s) (2) и вероятности (7) показывает, что нетривиальное влияние поля на процесс g ® a описывается параметром
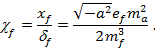
Будем считать «слабым» поле для которого 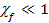 . Для фермионов е, u, d df >> 1 и, следовательно, величина
. Для фермионов е, u, d df >> 1 и, следовательно, величина 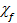 мала в очень широкой области изменения параметра интенсивности волны.
мала в очень широкой области изменения параметра интенсивности волны.
Случаи малого динамического параметра 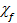 соответствует большому значению аргумента h функции Харди-Стокса в интеграле L (см. (6)), т. е.
соответствует большому значению аргумента h функции Харди-Стокса в интеграле L (см. (6)), т. е.
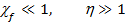
В пределе «слабого» поля входящая в выражение для вероятности перехода g ® a функция G существенно упрощается
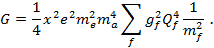
При этом вероятность и число переходов имеют вид:
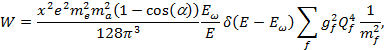
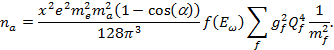
4. Предел «сильного» поля.
Рассмотрим экзотическую область 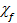 >> 1, соответствующую ультрарелятивистским энергиям распадающихся бозонов и относительно сильным электромагнитным полям. Будем условно называть «сильными» поля, для которых
>> 1, соответствующую ультрарелятивистским энергиям распадающихся бозонов и относительно сильным электромагнитным полям. Будем условно называть «сильными» поля, для которых 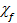 >> 1. И хотя в настоящее время экспериментальных возможностей создания таких условий нет, анализ этого случая может представлять интерес с точки зрения астрофизики.
>> 1. И хотя в настоящее время экспериментальных возможностей создания таких условий нет, анализ этого случая может представлять интерес с точки зрения астрофизики.
Случай большого динамического параметра 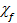 соответствует малому значению аргумента h функции Харди-Стокса, т. е.
соответствует малому значению аргумента h функции Харди-Стокса, т. е.
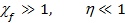
В этом случае:
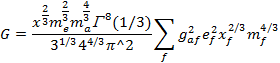
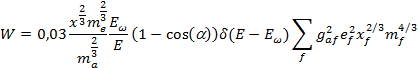
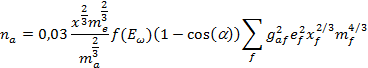
Заключение
В настоящей работе получены общие выражения для амплитуды и вероятности процесса, а также число переходов g ® a в единицу времени в единице объема. Полученные выражения позволяют получить любой член разложения по внешнему полю. Строгий учет влияния внешнего электромагнитного поля в пропагаторах заряженных фермионов позволяет исследовать данный процесс в области экстремально сильных полей, значения напряженностей, которые могут превосходить Швингеровские значения напряженностей. Результаты, полученные в данной работе, могут представлять большой интерес в той области астрофизики, где реализуются сильные электромагнитные. С другой стороны, эти результаты представляют, по нашему мнению, интерес в космологии ранней Вселенной. Рассмотренный переход фотон ® аксион может также играть роль дополнительного урка-процесса потери энергии звездами.
Выражение для вероятности процесса исследовано как в пределе «сильного», так и пределе «слабого» внешнего поля волны. Показано, что данный переход может иметь в обоих случаях резонансный характер. Получена оценка для числа переходов g ® a в наиболее интересном — в приложении к астрофизике и космологии — случае «сильного» поля.
Литература:
1. Василевская Л. А., Михеев Н. В., Овчинников О. С. О влиянии магнитного поля на время жизни аксиона // ЯФ.-1998. — Т. 61, N. 4.- C. 697–703.
2. Василевская Л. А., Михеев Н. В., Овчинников О. С. a ® e+e- decay in a model with indused coupling to leptons. a ® e+e- распад в модели с индуцированным взаимодействием с лептонами. // Modern Physics Letters A.- 1998.- V.13, N.4.- P. 321–326.
3. Василевская Л. А., Михеев Н. В., Овчинников О. С. Нейтринный распад псевдоскалярной частицы в магнитном поле. // ЯФ.- 1998. — T. 61, N. 9. — C. 1663–1669.
4. Василевская Л. А., Михеев Н. В., Овчинников О. С., Пархоменко А. Я. Индуцированное взаимодействие аксиона с электронами во внешнем магнитном поле. // ЯФ.- 1999.- Т. 62, N. 9.- С. 1662–1667.
5. Овчинников О. С. Осцилляторные явления в системе аксион-фотон во внешнем магнитном поле. Научная мысль Кавказа. — 2006. — Спецвыпуск № 2. — С. 111–116.
6. Овчинников О. С. Осцилляции аксион-фотон в поле плоской монохроматической электромагнитной волны. Научная мысль Кавказа. — 2008. — № 9. — С. 168–173.
7. Ovchinnikov O. Decay of a ultrarelativistic pseudoscalar particle in a magnetic field // Scientific enquiry in the contemporary world: theoretical basiсs and innovative approach. Vol. 1 Natural sciences. FL, USA, L&L Publishing. — 2012. — P. 20–25.
8. Peccei R. D. Quinn H. R. CP conservation in the presence of instantons. Phys. Rev. Lett.. 1977. V.38. P. 1440.
9. Peccei R. D. Quinn H. R. Phys. Rev., 1977. V.D1G, P.1791.

