Введение. Внастоящее время проектирование и строительство висячих мостов с высокой прочностью, эффективностью и в кратчайшие сроки является актуальной научно-практической задачей. Такое проектирование повышает надежность конструкций, снижает их стоимость, сокращает сроки строительства и позволяет внедрять современные архитектурные решения в городскую и сельскую среду [1].

При проектировании висячих мостов одних теоретических знаний недостаточно. Автоматизация расчетных процессов с использованием компьютерных технологий способствует созданию надежных и безопасных конструктивных решений [6]. Поскольку пролеты этих конструкций обычно большие, а основные несущие элементы изготовлены из высокопрочной стали, в таких конструкциях естественно возникают значительные прогибы.

Появление больших прогибов объясняется тем, что расчетное сопротивление канатов (стальных тросов), используемых в висячих мостах, в 4–7 раз больше, чем у традиционных профильных конструкций, а модуль упругости на 25 % меньше. Согласно закону Гука, напряжение в конструкции прямо пропорционально модулю упругости материала и относительным деформациям. Следовательно, канаты из высокопрочной стали под действием нагрузки обладают большей растяжимостью по сравнению с профильными элементами [9].

Цель и задачи исследования. Основная цель исследования-изучение основных принципов расчета висячих мостов с использованием аналитических и численных методов и их оценка на практических примерах. Это позволяет исследовать напряженно-деформационные состояния канатов и анкерных конструкций мостов, а также определить их геометрически нелинейное поведение.

Основные задачи исследования:

— Исследование трех типов мостов, расположенных в городе Самарканде, в качестве практических примеров: 132-метровый висячий вантовый мост через Даргомский канал, 101-метровый вантовый мост на улице Иджодкор и 50-метровый висячий мост через реку Ок Дарья.

— Оценка прочности и устойчивости канатов и анкерных конструкций.

— Использование программного комплекса ЛИРА-САПР и аналитических методов для анализа геометрически нелинейного поведения конструкций.

— Сравнение результатов аналитических и численных расчетов и предоставление практических рекомендаций.

Экспериментальные исследования и анализ результатов. Висследовании проанализированы реакции висячих мостов на статические и динамические нагрузки. Расчеты проводились с использованием следующих методов:

Методы расчета: При аналитическом (ручном) расчете висячих мостов и расчетах с помощью программного комплекса ЛИРА-САПР сравнивались стальные канаты с пролетами 30, 50, 80, 100, 120, 150, 170 и 200 метров. Для каждого каната определялись напряжения, прогибы до и после деформации.

а) Классический (аналитический) инженерный метод расчета [8].

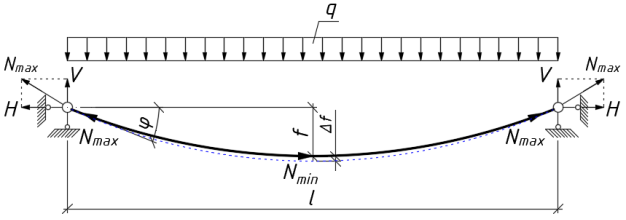
Рис. 1. Геометрическая схема стальных канатов висячего моста

Начальное прогибание каната:

здесь: f– начальное прогибание , l — пролёт. (1)

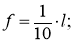
Без учета деформации каната формула для определения горизонтальной реакции опор H , вызванной напряжением в канате, определяется следующим образом:

здесь: q — постоянная нагрузка. (2)

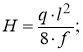
Вертикальная опорная реакция V, возникающая в канате, определяется следующим образом:

(3)

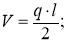
Максимальные N _max и минимальные N _min напряжения в канате вычисляются по формулам:

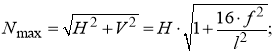
N _min =H; (4)

Поперечное сечение каната A определяется следующим образом:

здесь: R _{un —} временное сопротивление стальных канатов, (5)

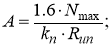
k _{n —} коэффициент, учитывающий растяжимость стальных канатов.

Прогиб Δ f каната от равномерно распределенной нагрузки определяется как: (6)

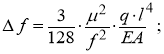
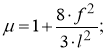
здесь: – коэффициент, учитывающий увеличение начального прогиба стальных канатов; E– модуль упругости стальных канатов; A– поперечное сечение стальных канатов.

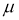
Длина каната до деформации при нахождении опор на одной плоскости:

(7)

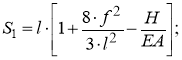
Длина каната после деформации при нахождении опор на одной плоскости:

(8)

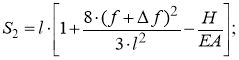
Угол наклона φ каната относительно горизонтали определяется как:

(9)

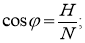
б) Численные методы (моделирование на компьютере).

С помощью данного метода конструкцию можно разделить на мелкие элементы, что позволяет точно вычислять и анализировать силы, смещения и деформации в каждом элементе. Для расчета современных висячих мостов применяются следующие численные методы [8].

В качестве примера рассмотрим процесс расчета стальных канатов висячего моста с пролетом 80 метров. Геометрическая схема стального каната представлена на рис. 2. Расчет каната под распределенную нагрузку 2 кН/м выполнялся с помощью программного комплекса ЛИРА-САПР, а результаты аналитического расчета представлены на рис. 3 и 4 [3].

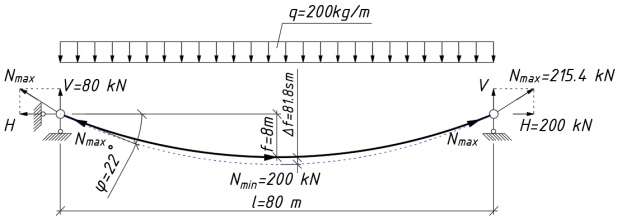
Рис. 2. Геометрическая схема висячего каната

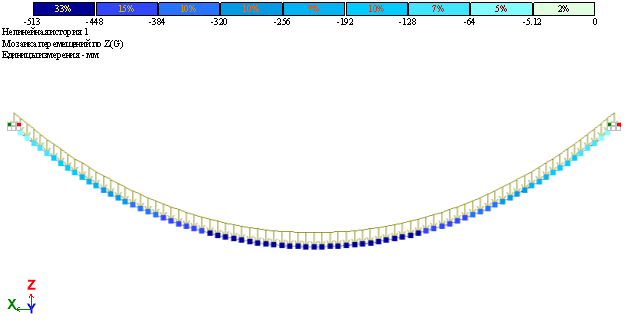
Рис. 3. Прогиб висячего каната после деформации

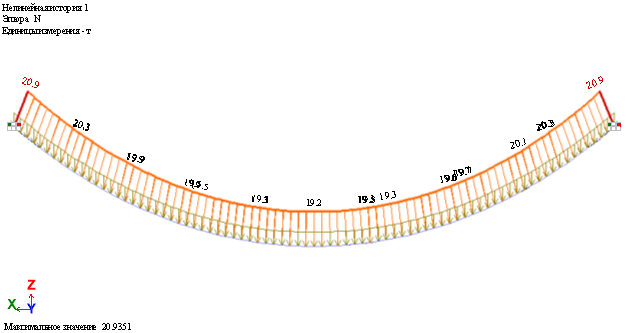
Рис. 4. Продольное напряжение N висячего каната после деформации

Таблица 1

в) Мониторинг и экспериментальный метод расчета

Для подвесных и вантовых конструкций необходимо наличие устройств для натяжения тросов (Ø16, Ø26) в узлах их крепления к пилонам и конструкциям проезда, с целью предотвращения неэластичных удлинений тросов в этих узлах после испытаний моста на максимальные нагрузки и в процессе эксплуатации [10].

Рис. 5. Диаметр — 16 мм. Испытание каната LK-RO 6x36 (1+7+7/7+14) + 7∙7(1+6) с помощью пресса

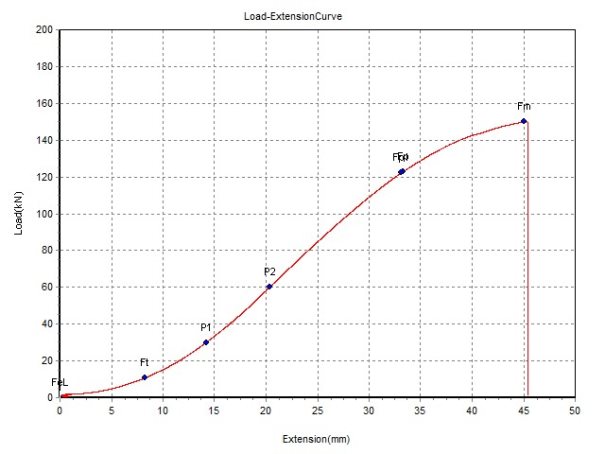
Рис. 6. График напряжение — деформация каната марки LK-RO в процессе испытания

Обсуждение. Экспериментальные, численные и аналитические исследования показали, что в стальных канатах висячих и вантовых мостов возникают различные напряжения и деформации в зависимости от длины моста, конструктивного решения и опорной системы. Результаты расчетов в программе ЛИРА-САПР и аналитические вычисления совпадают на высоком уровне, что подтверждает надежность методов расчета [2].

Например, на исследованном висячем вантовом мосту через канал Даргом (длина пролета 132 м) из-за большой длины пролета наблюдались максимальные удлинения и нелинейные деформации в стальных канатах. На вантовом мосту на улице Иджодкор (длина пролета 101 м) деформации относительно небольшие, а прочность высокая, поскольку здесь конструкция моста однопролетная и основные конструкции подвешены на вантах. На висячем мосту через Ок Дарья (длина пролета 50 м) деформации малы, однако конструктивная прочность требует проверки расчетом.

На такого рода мостах под воздействием различных нагрузок возникают значительные деформации. Сопоставление результатов расчетов в ЛИРА-САПР и аналитических данных подтверждает их соответствие и надежность методов.

Рис. 7. Мост через канал Даргом (132 м)

Рис. 8. Мост на улице Иджодкор (101 м)

Рис. 9. Висячий мост через реку Ок Дарья (50 м)

Полученные результаты практически помогают глубже понять характеристики напряжение–деформация мостов, оптимизировать проектирование и обеспечить безопасную эксплуатацию.

Заключение

Для расчета мостов и анализа состояния напряжений и деформаций в конструктивных элементах только аналитических методов недостаточно; численные методы существенно повышают точность расчетов. Экспериментальные методы имеют важное значение для обеспечения работоспособности, приоритетности и долговременной надежности мостов.

Причиной нелинейной работы мостов являются несущие элементы — ванты. После первоначального напряжения стальные канаты испытывают неупругое удлинение примерно на 4 %. При определении максимальной прогибаемости и напряжений канатов необходимо, чтобы аналитические формулы и результаты моделирования в программе ЛИРА-САПР совпадали.

Для уменьшения первоначального удлинения канатов их необходимо выдерживать в течение 72 часов под воздействием временного усилия, равного 50 % от расчетного сопротивления. Кроме того, для снижения прогибаемости висячих мостов можно уменьшить напряжение путем укорочения стержней, соединяющих проезжую часть с стальными канатами.

Современные компьютерные программы позволяют повысить безопасность и экономическую эффективность проектирования мостов.

Литература:

1. Вантовые мосты / А. А. Петропавловский [и др.]; под ред. А. А. Петропавловского. — М.: Транспорт, 1985. — 224 с.
2. Кирсанов Н. М. Висячие и вантовые конструкции / Н. М. Кирсанов. — М.: Стройиздат, 1981. — 158 с.
3. Сильницкий Ю. М. Расчет висячих мостов по деформированной схеме: учеб. пособие / Ю. М. Сильницкий. — Л.: ЛИИЖТ, 1967. — 207 с.
4. Барановский А. А. Мосты больших пролетов. Проектирование висячих и вантовых мостов: курс лекций / А. А. Барановский. — Санкт-Петербург: ПГУПС, 2005. — 272 с.
5. Бахтин С. А. Проектирование висячих и вантовых мостов: учеб. пособие / С. А. Бахтин. — Новосибирск: Сиб. ГАПС, 1995. — 121 с.
6. ШНК 2.05–02–07. Мосты и тоннели. «Автомобильные дороги», Госархитектстрой, г. Ташкент, 2008. — 90 с.
7. ШНК 2.03.05–13. «Металлоконструкции. Нормы проектирования» / Государственный комитет архитектуры и строительства Республики Узбекистан. — Ташкент, 2013. — 171 с.
8. Программный комплекс LIRA-SAPR®. Руководство пользователя. Под ред. академика РААСН Гордецкого А. С. — 2018. — 254 с.
9. Металлоконструкции. А. И. Холмуродов. (Часть 1. Расчет конструктивных элементов), учебное пособие. — Самарканд, 2023. — 182 с.
10. Металлоконструкции. А. И. Холмуродов. (Часть 2. Расчет и проектирование строительных конструкций), учебное пособие. — Самарканд, 2023. — 232 с.
11. Хасанов А. З., Хасанов З. А. Инженерная геология и механика грунтов. — Самарканд: Зарафшон, 2018.
12. Khasanov A. Z., Khasanov Z. A. Experimental and Theoretical Study of Strength and Stability of Soil. — 2020. Taylor & Francis Group, Boca Raton, London. — 139 p.
13. Дороган А. С. МГИУ для расчета балочно-комбинированных мостов // Современные технологии железнодорожного транспорта: материалы 44-й научной конференции. — Хабаровск: Изд-во ДВГУПС, 2006. — Т.2. — С. 20–26.
14. Аналитические методы расчета висячих и вантовых мостов: учеб. пособие / Ю. В. Дмитриев, А. С. Дороган. — Хабаровск: Изд-во ДВГУПС, 2008. — 194 с.: ил.
15. Товбоев Б., Юзбоев Р. К расчету элементов сельскохозяйственных сооружений, работающих в нестационарных условиях // Thematic Journal of Applied Sciences. — 2021. — Т. 1, № 1.