Деформационный расчет симметричных систем из упругих нитей с учетом влияния начального натяжения и перепада температур



В статье предложена и экспериментально апробирована методика определения провиса симметричных систем из упругих нитей от центральной нагрузки. Численным методом получена рабочая таблица, позволяющая наряду с провисом определить усилия в нити для проверки прочности подвесных систем по деформированному состоянию без применения сложного математического аппарата. Предложенная методика деформационного расчета позволяет учитывает влияние начального натяжения и перепада температур, что ведет к снижению риска аварий при эксплуатации подвесных (вантовых) систем.

Ключевые слова : деформационный расчет, провис, упругая нить, начальное натяжение, перепад температур.

Основные теоретические подходы сложились в первой половине XX века под влиянием массового строительства линий электропередач (ЛЭП). Большинство методик основано на аппроксимации уравнения цепной линии, описывающего деформированное состояние упругой нити от равномерных нагрузок. Соответствующие решения трансформированы в практические рекомендации по контролю провиса ЛЭП на стадии их монтажа.

Дальнейшее развитие этих методик нашло отражение в строительной отрасли, в частности при проектировании подвесных и вантовых конструкций. Основные усилия конструкторов были направлены на стабилизацию конструктивной формы от внешней нагрузки изменчивого характера, что, в свою очередь, породило множество различных конструктивных форм и соответствующих приближенных методик [1–3]. Стремление к стабилизации конструктивной формы отодвигало на второй план важность задачи определения провиса систем из упругих нитей (вантовых систем). В наиболее сложных случаях (мосты и большепролетные перекрытия на вантах, высотные мачты на оттяжках) деформационные расчеты выполняются на специализированных программных комплексах.

Таким образом сложилась ситуация, когда для достаточно широкого класса простых подвесных систем (канатных переправ, подвесок светофоров и контактных сетей над проезжей частью дорог, различного рода светильников над помещениями большой площади, спортивных тренажеров и т. п.) применяются указанные ранее приближенные решения, разработанные для стабильной конструктивной формы. Данный подход способен привести к значительным погрешностям определения деформированного состояния, возникновению непрогнозируемых усилий и, как следствие, к аварийным ситуациям. Зачастую обрыв троса приводит к человеческим жертвам [4]. Примечателен факт, что более 50 % аварийных ситуаций, по мнению авторов работы [5], происходят по причинам, не связанным с нарушением условий эксплуатации.

В связи с изложенным представляется целесообразным отдельно рассмотреть вопрос определения максимального провиса симметричных вантовых систем из упругих нитей, в которых величина сосредоточенной нагрузки превалирует над нагрузкой от собственного веса.

Теоретические положения. Рассмотрим нить из двух ( n=2 ) одинаковых ветвей l = 0,5∙L натянутую усилием N ₀ между опорами А и В (рис.1) и затем нагруженную силой P .

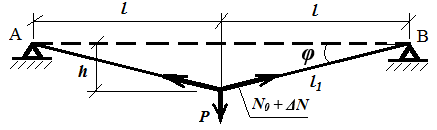
Рис.1. Расчетная схема упругой нити

Введем допущения: нить абсолютно невесомая и изготовлена из идеально упругого материала; изменение длины x = (l ₁ — l) вследствие растяжения мало по сравнению с начальной длиной; площадь поперечного сечения нити S при натяжении не уменьшается.

Условие равновесия сил в точке приложения силы P :

(1)

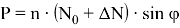
В рамках принятых допущений приращение усилия ΔN можно найти по формуле (2)

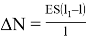
взависимости от площади поперечного сечения нити S и модуля упругости материала E . Заменяя отношение l / l ₁ косинусом угла φ, формулу (2) можно представить в следующем виде:

. (3)

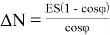
Подставляя (3) в условие (1), после несложных алгебраических преобразований получим окончательное уравнение равновесия в виде:

(4)

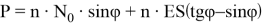
При n=2 обе ветви размешены в одной вертикальной плоскости, т. е. принадлежат одной нити. Легко видеть, что уравнение (4) применимо и для пространственных ( n>2 ) симметричных систем из одинаково натянутых ветвей, см. рис.2.

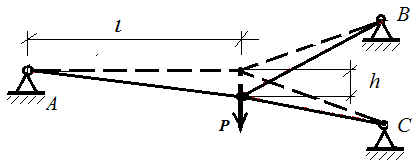
Рис. 2. Расчетная системы из упругих нитей при n = 3

Решив уравнение (4) относительно φ , можно определить искомое значение провиса по деформированной схеме

h = l∙ tg φ (5)

и усилие N в нити с учетом влияния начального натяжения N ₀

N = (6)

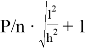
В реальных условиях начальное натяжение N ₀ вант (при P = 0) под влиянием изменения температуры окружающей среды может существенно отличаться от величины предварительного натяжения N _m , заданного при монтаже подвесной системы. С теоретической точки зрения учет влияния перепада температур сложностей не вызывает. При понижении температуры длина упругой нити укорачивается на величину

x = α∙l (t _m — t) , (7)

где α — коэффициент линейного расширения материала нити (1/град.),

t, t _m — конечная и начальная (монтажная) температура среды.

При неподвижно закрепленных концах из-за изменения длины, согласно закону Гука, в нити возникает дополнительное усилие N _t

N _t = x∙ES / l = α∙ES (t _m — t). (8)

То есть для учета влияния перепада температуры значение начального натяжения N ₀ для использования в уравнении (4) нужно предварительно вычислить в зависимости от монтажного усилия N _m и температуры t _m , зафиксированных на момент монтажа подвесной системы:

N ₀ = N _m + α∙ES (t _m — t). (9)

Уравнение (4) представляет собой зависимость угла φ (в радианах) от четырех параметров φ= F (P, N ₀ , E, S) . Для сокращения числа параметров воспользуемся методами теории подобия и размерностей. Как показано в [6, с.17], в соответствии с π-теоремой подобия в данном случае можно сократить число параметров до двух. Обозначим новые параметры:

— относительное удлинение нити от компоненты силы ;

— параметр относительного начального натяжения.

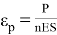
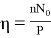
Подставив в уравнение (4) P =nES∙ε _p , nN ₀ = nES∙ε _p 𝜂 _, после преобразований получим зависимость угла φ = f (ε _p , 𝜂) от двух параметров:

ε _p = tg φ — sin φ ∙ (1 — ε _p 𝜂). (10)

Заметим, что произведение ε _p 𝜂 в правой части формулы представляет собой самостоятельную физическую величину ( ε _n ), характеризующую относительное удлинение нити от начального натяжения: ε _n = ε _p 𝜂 = N ₀ /(ES).

Для фиксированных значений деформаций от начального натяжения ε _n величина ε _p будет монотонно возрастать с увеличением угла φ от 0 до , поэтому для решения выбран алгоритм последовательных приближений методом бисекции. Зависимость тангенса угла φ от относительных параметров ε _p и 𝜂 , полученная на основе компьютерных вычислений, показана на рис.3, а соответствующие численные значения приведены в табл.1.

Как видно из графиков на рис.3 зависимость тангенса угла φ от параметров ε _p и 𝜂 имеет ярко выраженный нелинейных характер. Нелинейность в наибольшей степени проявляется при малых значениях параметра ε _р , лежащих примерно в диапазоне от 0 до 0,004. Именно этот диапазон интересен для решения практических задач конструирования подвесных систем с превалирующим значением сосредоточенной полезной нагрузки по сравнению с собственным весом упругой нити.

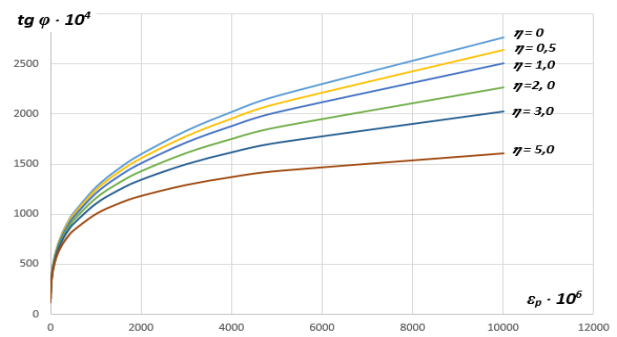
Рис. 3. Зависимость тангенса угла наклона нити от параметров ε _р и 𝜂

Экспериментальная оценка . Измерения провиса проведены в условиях обычной общеобразовательной школы. Для испытаний выбраны следующие материалы: резиновый жгут диаметром 10 мм, состоящий из пучка тонких резинок в тканевой оплетке и стальная проволока диаметром 0,6 мм. В качестве груза применялись пластиковые бутыли номинальной емкостью 1,5 л — массой 43 г. и емкостью 4,0 л — массой 91 г., в которые доливался нужный объем воды. Плотность воды принята равной 1,0 кг/л, а ускорение свободного падения для перевода усилий в систему единиц СИ — 9,80665 м/с2. Значение модуля упругости для резинового жгута E = 1,835 МПа принято по результатам натурных измерений, а для стальной проволоки принято табличное значение E = 200 ГПа.

Испытание на провис упругой системы из резиновых жгутов проведены по Y -образной схеме , т. е. при n=3. Концы первого жгута закреплялись неподвижно. Один конец второго жгута зацеплялся за середину первого, а второй конец натягивался с помощью противовеса (пластиковая бутыль) таким образом, чтобы точка соединения жгутов совпала с заранее размеченным геометрическим центром системы (рис. 4). Таким образом создавалась система из 3-х равномерно натянутых упругих нитей, расположенных под углом 120 ⁰ друг к другу. Величина начального натяжения определялась массой противовеса, который убирался после закрепления третьей ветви струбциной. Проведено две серии измерений: при начальном натяжении N ₀ = 15,1 Н ( l = 640 мм), N ₀ = 21,0 Н ( l = 670 мм). Результаты испытания и сравнение с теоретическими данными показаны на рис.5.

Рис. 4. Испытание Y-образной упругой системы: а) общий вид; б) измерение провиса

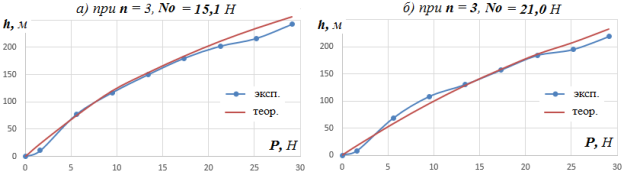
Рис. 5. Зависимость провиса h центра системы из 3-х резиновых жгутов от силы P

Воздействие перепада температур исследовалось при испытании стальной проволоки . Проведено 4 серии измерений. Две первых серии испытаний выполнены для проволоки длиной 18,68 м, натянутой монтажным усилием N _m ≈ 40,13 Н. Вначале были сняты показания днем при температуре окружающей среды t _m = +10 ⁰ С, а затем, не меняя натяжения проволоки — ранним утром следующего дня при температуре t = -1 ⁰ С.

Две следующие серии измерений сделаны для проволоки длиной 15,23 м, натянутой ранним утром усилием N _m ≈ 10,70 Н. Замеры провиса сначала выполнены при температуре t _m = -1 ⁰ С, а затем — в полдень — при t = +9 ⁰ С. Таким образом перепад температур в первом случае составил +11 ⁰ С в первом случае, и -9 ⁰ С — во втором. Общий вид (с неснятым противовесом) и измерение провиса показаны на рис.6. Графики зависимости стрелки провиса от величины центральной нагрузки P с учетом влияния перепада температур в сравнении с теоретическими данными приведены на рис. 7.

Рис. 6. Испытание стальной проволоки: а) общий вид; б) зажим; в) измерение провиса

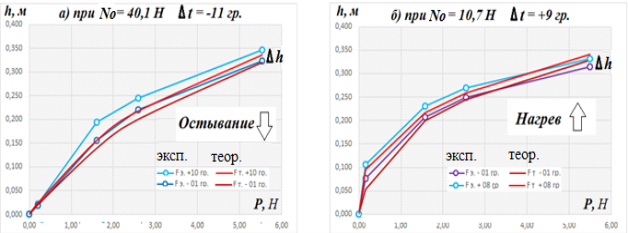
Рис. 7. Зависимость провиса h от силы P в условиях перепада температур

Как видно из графиков на рис. 5, 7 теоретические значения стрелки провиса вполне удовлетворительно согласуются с экспериментальными данными, что говорит о возможности применения на практике значений тангенса угла φ от относительных параметров ε _p и 𝜂 , приведённых в табл.1.

Таблица 1

Таблица значений tg φ для расчета стрелы провиса

ε p ∙10 6	Значения tg φ ∙10 4 при 𝜂 , равном:
	0	0,1	0,25	0,5	1	2	3	5	10	15	20
1	126	126	126	126	125	125	124	123	121	118	115
2	159	159	159	158	158	157	156	155	150	146	142
3	182	182	182	181	181	180	178	176	171	165	160
4	200	200	200	199	199	197	196	193	187	180	174
5	215	215	215	215	214	212	211	208	200	192	185
10	271	271	271	270	269	267	264	259	247	235	223
15	311	311	310	309	308	304	302	295	279	263	248
20	342	342	341	340	338	334	330	323	303	284	266
30	392	391	390	389	387	381	376	366	341	316	292
40	431	430	430	428	425	419	413	400	370	340	311
50	464	464	463	461	457	450	443	429	393	359	326
100	585	584	582	580	574	562	551	528	473	420	372
150	670	669	666	663	655	640	625	596	523	456	397
200	738	736	733	729	720	702	683	648	561	481	413
300	845	843	839	833	821	797	774	727	615	515	433
400	930	927	923	916	901	873	844	787	654	538	445
500	1003	999	994	986	969	936	902	837	683	554	454
1000	1265	1260	1252	1238	1212	1159	1106	1003	773	597	474
1500	1450	1443	1432	1415	1380	1310	1241	1108	820	616	482
2000	1597	1589	1576	1555	1512	1428	1345	1185	850	627	486
3000	1832	1821	1804	1776	1721	1610	1501	1295	888	639	491
4000	2020	2007	1986	1952	1884	1750	1619	1374	910	646	493
5000	2180	2164	2140	2101	2022	1866	1714	1434	925	650	495
10000	2765	2740	2701	2638	2511	2263	2027	1611	960	659	498
15000	3183	3150	3099	3015	2848	2523	2217	1702	974	662	499
20000	3522	3481	3419	3316	3112	2717	2353	1760	981	663	499
30000	4069	4014	3931	3794	3524	3006	2542	1830	989	665	500
40000	4515	4447	4346	4178	3846	3219	2670	1872	993	666	500
50000	4901	4821	4702	4504	4116	3388	2766	1900	995	666	500
100000	6376	6242	6042	5712	5069	3919	3030	1963	1000	667	500

Пример 1. Под куполом цирка смонтирована Y-образная система из 3-х стальных тросов диаметром d = 8 мм, расположенных под углом 120 ⁰ друг к другу, см. рис.8. Тросы натянуты начальным усилием N ₀ = 200 Н таким образом, что перекрывают здание цирка диаметром D = 50 м, и точка их взаимного соединения находится точно над центром арены. К этой точке подвешен канат акробата. Найти величину провиса h от акробата весом P = 700 Н. Модуль упругости тросов принять равным E = 140 ГПа, собственным весом тросов и подвешенного каната пренебречь.

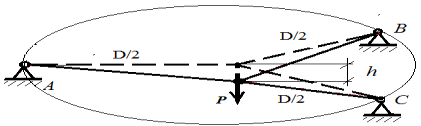
Рис. 8. Схема подвеса каната акробата

Решение. Вычисляем параметры натяжения:

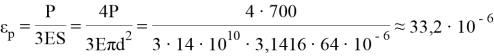
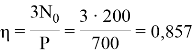
По таблице 1 находим tg φ ≈ 0,400

Величина провиса = 1,0 (м).

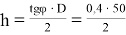
Пример 2. Над рекой 7-го класса судоходности (вертикальный габарит для прохода судов не менее 7 метров) организована канатная переправа реверсного типа пролетом 240 м, см.рис.9. Стальной канат диаметром d = 32 мм при t _m = 0 ⁰ С натянут монтажным усилием N _m = 320 кН таким образом, что расстояние от точки подвеса грузовой тележки до максимального уровня воды в реке составляет 16 м. Необходимо проверить запас провиса из условия непрерывного обеспечения габарита для прохода судов при t = +40 ⁰ С, и запас прочности каната при t = -40 ⁰ С, если предельная прочность каната на разрыв составляет [N] = 500 кН, а максимальная вес грузовой тележки (вместе с полезным грузом) P = 55 кН. Модуль упругости каната принять E = 140 ГПа, коэффициент температурного расширения α = 0,000012 1/гр.С. Собственным весом каната пренебречь (учтен в собственной массе грузовой тележки).

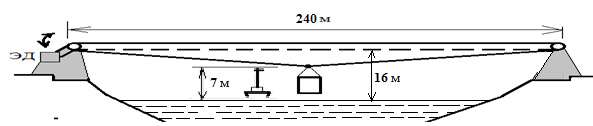
Рис. 9. Схема канатной переправы

Решение. Особенность данной схемы состоит в том, что растяжению подвержена весь трос длиной 2 ∙ 240 = 480 м, а провисает лишь нижний участок длиной 240 м. Поэтому принимаем длину ветви l = 240 / 2 = 120 м, а в качестве продольной жесткости ES при деформационном расчете будем принимать половину фактической величины ES = 140∙10 ⁹ ∙ π∙d ² /4 = 112600000 Н. Таким образом величина параметра ε _р равна:

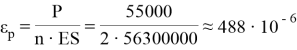
Максимальный провис возникает при положении грузовой тележки в середине пролета и t = + 40 ⁰ С. Натяжение с учетом нагрева до t = +40 ⁰ С:

N ₀ = 320000 + 0,000012∙112600000∙(0–40) ≈ 266000 (Н).

Параметр начального натяжения:

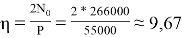
При ε _р = 488∙10– ⁶ и 𝜂= 9,67 из таблицы 1 находим tg φ ≈ 0,0690.

Тогда провис h = 120 ∙ 0,0690 = 8,28 (м).

Запас по габариту (16–7–8,28) = 0,72 (м) или 0,72/7∙100 % = 10,3 %.

Максимальное усилие в тросе будет при положении грузовой тележки в середине пролета и t = — 40 ⁰ С. Натяжение с учетом остывания до t = -40 ⁰ С:

N ₀ = 320000 + 0,000012∙112600000∙(0+40) ≈ 374000 (Н).

Параметр начального натяжения:

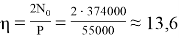
При ε _р = 488∙10– ⁶ и 𝜂= 13,6 из таблицы 1 находим tg φ ≈ 0,0588.

Провис h = 120 ∙ 0,0588 = 7,06 (м), а соответствующее усилие в тросе:

≈ 468000 (Н) ≈ 468 кН.

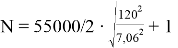
Запас по прочности троса: (500–468) /500 ∙ 100 % = 6,4 %.

Заключение. Применение методов теории подобия и размерностей позволило выявить два базовых параметра (ε _р и 𝜂), характеризующих нелинейную связь провиса h предварительно натянутой симметричной системы из упругих нитей от центрально приложенной внешней нагрузки P . На основе численных расчетов сформирована расчетная таблица, позволяющая вычислять провис и максимальное усилие в нити с помощью обычного калькулятора. Немаловажным фактором при этом является возможность учета влияния перепада температур, который в условиях сурового климата России может достигать 80 ⁰ С и более.

Литература:

1. Кирсанов Н. М. Висячие и вантовые конструкции. — М.: Стройиздат, 1981. — 217 с.
2. Рекомендации по проектированию висячих конструкций / утв. ЦНИИСК им. В. А. Кучеренко 12 мая 1972 г. — URL: http://docs.cntd.ru/document/1200075325
3. Приближенный расчет вантовых конструкций/ Строительно-информационный портал — 12 сентября 2020г. — URL: http://fccland.ru/prostranstvennye-konstrukcii/10825-priblizhennyy-raschet-vantovyh-konstrukciy.html.
4. Статистика НС за 60 лет на канатных дорогах горнолыжных курортах мира / Проект Alp -2011г. — URL: http://alp.org.ua/?p=21730.
5. Анализ аварийных ситуаций на канатных дорогах и повышение безопасности при эксплуатации канатных дорог / К. Л. Голубь, Л. Ю. Гузова, А. А. Григорьян [и др.] // Техника. Технологии. Инженерия. — 2018. — № 1 (7). — стр. 29–32. — URL: https://moluch.ru/th/8/archive/76/3014/.
6. Архипов В. А., Коноваленко А. И. Практикум по теории подобия и анализу размерностей. -Томск: ТГУ, 2016. — 92 с.