Вычислительная техника современности позволяет выполнить расчет различных строительных конструкций с учетом разного рода аспектов, таких, например, как учет нелинейных свойств материалов, условий закрепления и т. д. Задействовав метод конечных элементов, заложенный в нелинейном процессоре ПК «Лира-САПР 2017», автор в своей работе провел численный эксперимент, который может заменить натурный эксперимент, требующий куда больших временных и материальных ресурсов. Стоит помнить, что развитие методов математического моделирования строительных конструкций является одним из важнейших направлений современной строительной науки. Автором проведено численное исследование на конечно-элементных моделях, были получены схемы разрушения, распределения касательных напряжений и распределения деформаций по высоте нормального сечения сталефибробетонного элемента.
Ключевые слова: сталефибробетон, бетон, фибра, композиционный материал, бетон, конструкция.
Как известно по работам зарубежных и отечественных ученых, добавление стальной фибры меняет характер разрушения образцов. При образовании трещин при разрушающей нагрузке, опытный образец оставался целым. Из этого было выдвинуто предположение, что при срезе сталефибробетонной балки фибра так же будет влиять на возникающие внутренние усилия и работу конструкции в целом.
Суть эксперимента заключается в моделировании балки в плоской задаче. Как нам известно значение поперечной силы при расчете по наклонному сечению ж.б балки Q=Qb+Qsw. Согласно СП 360.1325800.2017 [1] расчет ведется аналогичным образом, за исключением значения Rfbt. Целью моделирования является нахождения значений поперечной силы получаемой при использовании сталефибробетона вместо обычного бетона. Предположим, что Q=Qb+Qsw+Qf. Предполагается получить значения касательных напряжений и, зная о прямой зависимости τxот Q, найти Qf.
В качестве расчетной схемы принималась половина балки длиной 600 мм. От вертикальных перемещений по оси Z закреплялось нижнее сечение балки. Используемая расчетная схема представлена на рисунке 1.
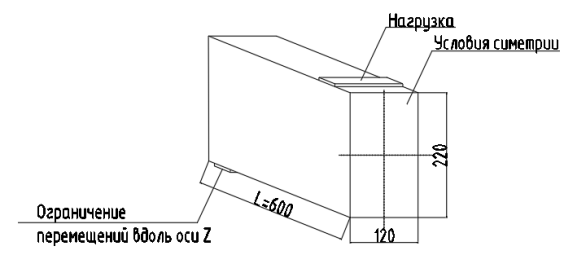
Рис. 1. Расчетная схема (рисунок авторов)
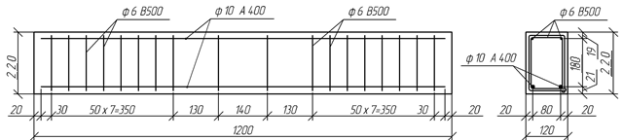
Рис. 2. Схема армирования балки (рисунок авторов)
Расчетная модель представляет собой однопролетную шарнирно-опертую балку. Нагрузка приложена в виде распределенных сил. Модель состоит из квадратных конечных элементов (КЭ) плоской задачи (балка — стенка) размерами — 5×5 мм, позволяющих моделировать плоское напряженное состояние.

Рис. 3. Общий вид замоделированной балки (рисунок авторов)
Для того чтобы смоделировать сталефибробетон в нелинейной постановке были использованы следующие типы КЭ: для арматуры — КЭ тип 210 (физически нелинейный универсальный стержневой элемент), для сталефибробетона — тип 231 — физически нелинейный параллелепипед размерами 0,01х0,01х0,01 (м). Так же контакт окружающего фибробетона и арматуры считается абсолютный.
На балку прикладываплась нагрузка с шагом 10 кН передавалась через специальные грузораспределительные пластины КЭ тип 41 с толщиной 50 мм, для них был принят упругий закон деформирования. При моделировании получили общее число КЭ –5142, общее число узлов –10922.
Задание сталефибробетона проводилось на основании экспериментальных данных, полученных в работе Евдокимовой Т. С. [2]. Рассматривалсь различное количество добавляемой фибры от 1 % до 2 %.
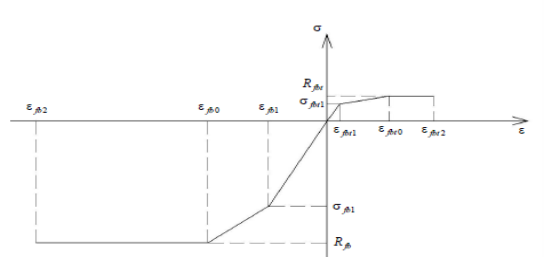
Рис. 4. Принятая диаграмма деформирования фибробетона
Где Rfb – расчетное сопротивление сталефибробетона на сжатие;
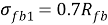
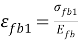
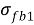
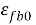
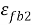
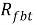
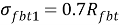
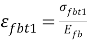
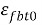
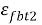
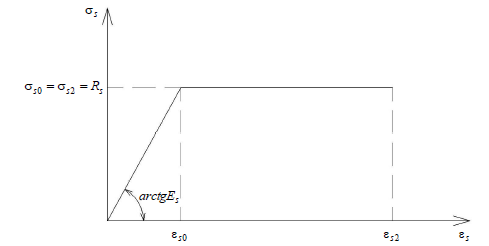
Рис. 5. Принятая диаграмма деформирования арматуры
Моделировались наклонные трещинины с помощью расшивки узлов, на основании эксперементальных данных из работы Филатова В. Б. [3], после достижения в КЭ напряжений, превышающих 1,75Rfbt в момент образования, и Rfbt в процессе развития трещин. Данный способ моделирования трещин позволил образовывать трещины в местах возникновения максимальных растягивающих напряжений и развивать их в соответствии с положением площадок главных растягивающих напряжений. Это позволило наиболее точно смоделировать напряжённое состояние сталефибробетона в вершине трещины и определить ее направление (рисунок 6).

Рис. 6. Схема трещинообразования в сталефибробетонной балке (рисунок авторов)
В результате численного эксперимента автором были получены изополя напряжений, изополя перемещений. С учетом принципа Сен-Венана изополя напряжений и перемещений рассматривались в зоне образовавшихся трещин.

Рис. 7. Пример полученных результатов τx(рисунок авторов)
Вывод
В данной работе проводилось сравнение значений τxв зоне раскрытия трещин, а именно возникающих в арматуре. Так как касательные напряжения имеют прямую зависимость от поперечной силы, то исходя из полученных результатов работа сталефибробетонной балки с содержанием фибры (1 %) улучшает работу на действие поперечных сил примерно на 27,2 %. C содержанием фибры (1,5 %) улучшает работу на действие поперечных сил примерно на 28,9 %. А вот с содержанием фибры (2 %), наоборот, видим ухудшение до 26,5 %. Результаты представлены в таблице 1.
Таблица 1
|
Номер участка |
Значения τ xy , кН/м2 Бетон B 25 |
Значения τ xy , кН/м2 Фибра 1 % |
Значения τ xy , кН/м2 Фибра 1,5 % |
Значения τ xy , кН/м2 Фибра 2 % |
|
1 |
15,9 |
17,4 |
17,4 |
17,5 |
|
2 |
22,8 |
11,2 |
10,8 |
11,3 |
|
3 |
12 |
10,9 |
10,8 |
11 |
|
4 |
13,4 |
8,79 |
8,59 |
8,86 |
|
5 |
12,5 |
9,16 |
9,06 |
9,21 |
|
6 |
9,38 |
11,1 |
11,1 |
11,1 |
|
7 |
14,9 |
8,35 |
8,04 |
8,41 |
|
8 |
8,63 |
9,09 |
9,08 |
9,16 |
|
Среднее значение |
13,68 |
10,75 |
10,61 |
10,81 |
|
% |
- |
27,2 % |
28,9 % |
26,5 % |
Литература:
- Свод правил СП 360.1325800.2017. Конструкции сталефибробетонные. Правила проектирования. / АО «НИЦ «Строительство». М.: 2017.
- Евдокимова Татьяна Сергеевна. Напряженно-деформированное состояние и расчет прочности кососжимаемых фиброжелезобетонных элементов: диссертация... кандидата Технических наук: 05.23.01 / Евдокимова Татьяна Сергеевна; [Место защиты: ФГБОУ ВО Санкт-Петербургский государственный архитектурно-строительный университет], 2017.- 150 с.
- Филатов В. Б., Коваленко М. В. Моделирование работы сборно-монолитной железобетонной балки в зоне поперечного изгиба // Вестник Евразийской науки, 2020 № 3, https://esj.today/PDF/57SAVN320.pdf (доступ свободный). Загл. с экрана. Яз. рус., англ.

