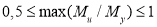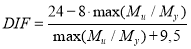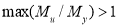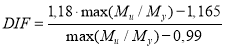При проектировании согласно действующим ГОСТ и СП для зданий и сооружений класса КС-3, а также класса КС-2 с массовым нахождением людей необходимо рассчитывать конструкции на аварийные и особые воздействия, ведущие к прогрессирующему обрушению. Расчеты на прогрессирующее обрушение ведутся с учетом динамического коэффициента. В зависимости от методики расчета коэффициент может приниматься равным константе, либо вычисляться по эмпирическим формулам. Существуют несколько различных способов вычисления коэффициента динамичности как в зарубежном, так и в отечественном проектировании.
Ключевые слова: прогрессирующее обрушение, коэффициент динамичности, линейно-статический расчет, нелинейно-статический расчет, динамический нелинейный расчет.
Расчет зданий и сооружений на непропорциональное обрушение нормируется российской и зарубежной обязательной строительной документацией. Непропорциональное обрушение это характеристика величины разрушения. Механизм разрушения может быть различным, например прогрессирующее (лавинообразное) разрушение [1]. Прогрессирующее разрушение возникает вследствие воздействия аварийных нагрузок [2], которые необходимо учитывать на стадии проектирования. Однако, учесть все факторы в ходе такого разрушения достаточно затруднительно, несмотря на возможности современных расчетно-вычислительных комплексов.
Наиболее распространенным методом расчета здания на прогрессирующее обрушение является описанный в нормах США [3] метод Альтернативных путей. Он позволяет не учитывать причину возникновения разрушения, в отличии от Косвенного метода, который подразумевает либо защиту конструкции от конкретных чрезвычайных ситуаций за счёт превентивных мер, либо создание избыточных связей для повышения статической неопределимости. Кроме того, метод Альтернативных путей включает три различных методики расчета:
— Линейный статический расчет (LSP);
— Нелинейный статический расчет (NSP);
— Нелинейный динамический расчет (NDP).
Основная идея расчета по методу Альтернативных путей заключается в том, что здание при аварийном воздействии и выключении из работы одного или нескольких несущих элементов, разрушалось до заданного состояния, например, с сохранением эксплуатационных качеств сразу после разрушения или после восстановления.
Для статических расчетов предусмотрено использование коэффициента динамичности для учета динамического фактора, что упрощает расчет, одновременно приближая его результаты к наиболее точному нелинейному динамическому расчету.
Величина динамического коэффициента в статических расчетах — это ключевое значение. Одна из самых ранних работ по определению коэффициентов динамичности при прогрессирующем обрушении — статья группы ученых Ruth P., Marchand K. и Williamson E [4]. В ней было были проанализировано влияние увеличения нагрузки на параметры, характеризующие пластические деформации при нелинейном статическом и нелинейном динамическом расчетах. В результате было определено, что пластичность имеет наибольшее влияние на коэффициент. Данный вывод в следующем исследовании, публикация Stevens D., Crowder B., Hall B. и Marchand K. [5], позволил определить характер зависимости динамического коэффициента от параметра пластических деформаций. На основе данных исследований в 2009 году McKay A. представил формулы по расчету динамического коэффициента, вошедшие в нормы США.
В настоящее время в нормах США [3] величина динамического коэффициента учитывается в зависимости от некоторых факторов:
— Назначение, тип и материал рассчитываемого элемента конструкции — первичный или вторичный элемент;
— Способ нагружения здания после удаления несущего элемента — pulldown и pushdown.
Для различных методик приведены следующие коэффициенты динамичности:
Для линейного статического расчета:
— при расчете параметров НДС по деформациям;
— при расчете параметров НДС по усилиям.
В общем случае данные коэффициенты обозначаются как LIF (LoadIncreaseFactor).
Для нелинейного статического расчета:
— DIF (DynamicIncreaseFactor).
Существует иной подход к расчету коэффициента динамичности, основанный не только на пластических деформациях, но и на существующих запасах поврежденной конструкции. Такой подход рассмотрен в исследовании Liu M [6]. Если здание рассчитано на восприятие значительных кратковременных нагрузок, то при удалении колонны его конструкции могут не достигнуть пластики, следовательно расчеты по формулам, учитывающим пластические деформации будут некорректны, так как в случае упругих деформаций динамический коэффициент условно равняется 2.
Однако запасы конструкций можно учесть, анализируя пластичность конструкции, полученную после приложения увеличенных на коэффициент динамичности нагрузок.
Стоит заметить, что на основе исследования влияния запасов конструкции авторами Saffari H. и Mashhadi J. [7] были выведены формулы коэффициентов DIF для pulldown-анализа железобетонных рам. Формулы зависят от параметра max(Mu/My), который характеризует степень нагруженности конструкции весовыми нагрузками GLA (Gravity Load Amplifier).
|
При
|
|
|
При
|
|
где
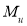
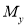
В линейных статических расчетах также существует альтернативный подход на основе частичного pulldown анализа, не входящий в нормативную базу, разработанный Mahmoudi M., Teimoori T. и Kozani H [8]. Подход заключается в том, что в месте удаления колонны верхнему узлу сообщается вынужденное перемещение
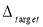
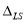
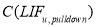
Динамический коэффициент определяется по нижеприведенным формулам.
Для внутренней колонны:
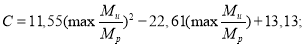
Для внешней колонны:
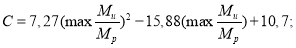
где
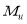
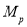
Если
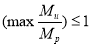
Данный метод также учитывает не только пластичность элементов, но и весовые нагрузки GLA (Gravity Load Amplifier).
В отечественных исследованиях динамический коэффициент часто выражается формулой [9]:
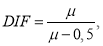
где
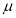
Для расчетов в упругой стадии
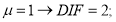
Для расчетов в пластике
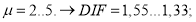
Однако Расторгуев Б. С., выводя эту формулу в своих работах принимал, что все ригели над удаляемой колонной в расчетной схеме имеют одинаковую деформируемость. Позже, чтобы учесть, разность наступления пластических деформаций в ригелях в каркасах высотой более 10 этажей Као Зуй Кхой было предложено уточнение [10]:
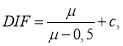
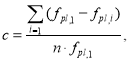
где
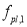
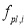
n — общее число этажей каркаса, i = 1… n .
Данное уточнение позволяет учитывать неодинаковость работы ригелей при расчете методом pulldown не только в пластической, но и в упругой стадии вне зависимости от количества этажей.
Литература:
1. Грачев В. Ю., Вершинина Т. А., Пузаткин А. А., Непропорциональное разрушение. Сравнение методов расчета. Екатеринбург, Издательство «Ажур», 2010,
2. СП 296.1325800.2017 Здания и сооружения. Особые воздействия. М.: ЦНИИСК им. В. А. Кучеренко при участии АО МНИИТЭП, ФГБУ «ГГО им. А. И. Воейкова», 2017.
3. UFC 3–340–02 Structures To Resist The Effects Of Accidental Explosions, With Change 2, 2008.
4. Ruth P., Marchand Kirk A., Williamson Eric B., «Static Equivalency in Progressive Collapse Alternate Path Analysis: Reducing Conservatism while Retaining Structural Integrity». Journal of Performance of Constructed Facilities Vol. 20, Issue 4 (November 2006). https://doi.org/10.1061/(ASCE)0887–3828(2006)20:4(349)
5. Stevens D., Crowder B., Hall B., Marchand K. «Unified progressive collapse design requirements for DoD and GSA», Structures Congress 2008, Vancouver, Canada, April 24–26, 2008.
6. Liu M. «A new dynamic increase factor for nonlinear static alternate path analysis of building frames against progressive collapse», Engineering Structures, 2013, Vol. 48, pp. 666–673.
7. Saffari H., Javad Mashhadi J. «Effects of damping ratio on dynamic increase factor in progressive collapse», Steel and Composite Structures 22(3):677–690 · October 2016, DOI: 10.12989/scs.2016.22.3.677
8. Mahmoudi M., Teimoori T., Kozani H. «Presenting displacement-based nonlinear static analysis method to calculate structural response against progressive collapse». International Journal of Civil Engineering, Vol. 13, No. 4A, Transaction A: Civil Engineering, December, 2015
9. Алмазов В. О., Плотников В. О., Расторгуев Б. С. «Проблемы сопротивления здания прогрессирующему разрушению». 2/2011, ВЕСТНИК МГСУ.
10. Као Зуй Кхой. Динамика прогрессирующего разрушения монолитных многоэтажных каркасов. Автореферат на соискание степени к. т.н., МГСУ, Москва, 2010.