Рассматривается пример моделирования результатов частных случаев решения задачи по определению номинальных величин геометрических параметров симметричных структурных схем механизмов с замкнутой системой тел качения (ЗСТК) с диаметрами равной величины.
Ключевые слова: механизм с замкнутой системой тел качения с диаметрами равной величины, механизм-прототип, эксцентриковый механизм качения, тела качения, сепаратор, дорожка качения, геометрические параметры, зазор между телами качения.
Обеспечение требуемых величин показателей качества механизмов приводов технологического оборудования является одним из приоритетных направлений модернизации и развития промышленного потенциала России. Достижение данной цели возможно только посредствам комплексного решения задач по определению величин геометрических параметров новых видов механизмов приводов технологического оборудования. К подобным механизмам относятся механизмы с замкнутой системой тел качения (ЗСТК), которые могут содержать в своей структуре тела качения с диаметрами как равной, так и разной величины. Механизм с ЗСТК с диаметрами равной величины является механизмом-прототипом для эксцентрикового механизма качения (ЭМК) как с зазором между телами качения, так и без данного параметра, который также может быть классифицирован как механизм с ЗСТК с диаметрами разной величины. Для ЭМК характерно смещение центров дорожек качения колец относительно друг друга на величину эксцентриситета и наличие замкнутой системы тел качения с диаметрами разной величины [1]. Тела качения механизмов данного вида могут обладать или гладкими рабочими поверхностями (фрикционные) [1…12] или поверхностями с выступами (зубчатые) [13…19]. Коллектив авторов проводит теоретические и экспериментальные исследования геометрических и кинематических параметров исполнительных механизмов технологического оборудования разработанного на базе механизмов данного вида с диаметрами разной (эксцентриковые) [1, 2, 9…11, 14…18] или равной (соосные) [3…8, 12, 13, 19] величины. В процессе реализации данных исследований было установлено, что задача по определению величин номинальных значений геометрических параметров механизмов с замкнутой системой тел качения равной величины является не линейной и при начальных условиях, что все исходные параметры постоянные величины и больше нуля, может не иметь решения, т. е.
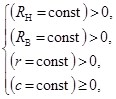(1)
где RВ и RН — радиусы дорожек качения внутреннего и наружного колец; r — радиус тел качения; 
— зазор между телами качения.
Для исключения подобных ситуаций в работах [3…8] авторами сформированы области существования и составлена расчетная модель механизмов с ЗСТК с диаметрами равной величины как с зазором между телами качения, так и без данного параметра (рис. 1), где 
, 
— дорожки качения внутреннего и наружного колец; ОВ и OН — геометрические центры дорожек качения внутреннего и наружного колец; С — сепаратор (водило); r0, r1, ri и 
, 
, 
— радиусы и углы положения тел качения. Области существования используются для выбора величин исходных данных необходимых для решения задачи по определению величин номинальных значений геометрических параметров. Для решения системы (1) необходим ввод поправки в расчет, считая, что один из исходных параметров является величиной переменной. Вариация значениями радиуса тел качения и зазора не позволяет достичь требуемого результата. В этом случае получаем, что решение этой задачи возможно по двум направлениям ввода поправки в расчет геометрических параметров, т. е. 
или 
, тогда система начальных условий (1) претерпит некоторые изменения
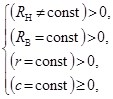(2)
или
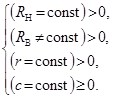(3)
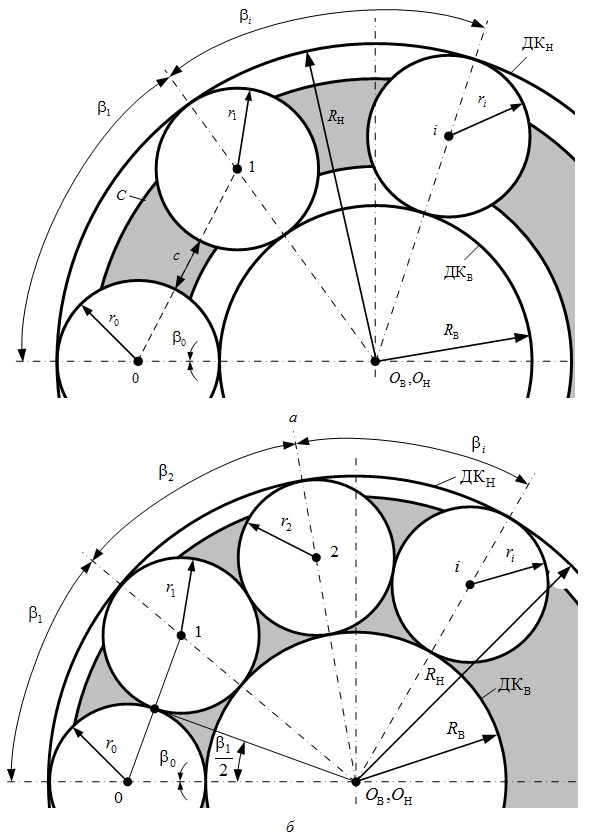
Рис. 1. Расчетная модель механизма с замкнутой системой тел качения с диаметрами равной величины
Каждая из систем (2) или (3) в зависимости от наличия или отсутствия зазора между телами качения получит два возможных варианта решения. Для механизма с ЗСТК с диаметрами равной величины с зазором системы (2) и (3) примут вид
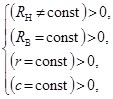(4)
или
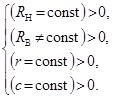(5)
При реализации структуры механизма с ЗСТК с диаметрами равной величины без зазора между телами качения системы (2) и (3) будут выглядеть как
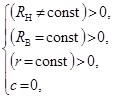(6)
или
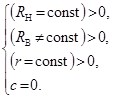(7)
С целью подтверждения правильности разработанного метода проведем решение систем (4)…(7) для механизмов с ЗСТК с диаметрами равной величины для обоих направлений ввода поправки как при наличии зазора между телами качения, так и при отсутствии в структуре данного параметра. Вычисления выполняем, варьируя значениями радиусов дорожек качения наружного и внутреннего колец в интервале (55…100), числом тел качения в диапазоне (0…100) и величиной зазора между этим звеньями в интервале (2…10) мм. Для повышения эффективности выполняемых расчетов авторами разработано программное обеспечение, которое представляет собой программный комплекс «Эксцентрик» зарегистрированный в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности (РОСПАТЕНТ) [20].
По полученным результатам выполняем компьютерное моделирование всех вариантов симметричных структурных схем механизмов с ЗСТК с диаметрами равной величины для обоих направлений ввода поправки как при наличии зазора между телами качения (рис. 1, а), так и при отсутствии в структуре данного параметра (рис. 1, б). Примеры результатов приводим при наличии зазора на (рис. 2, а…г), а при отсутствии в структуре данного параметра на (рис. 2, д…з).
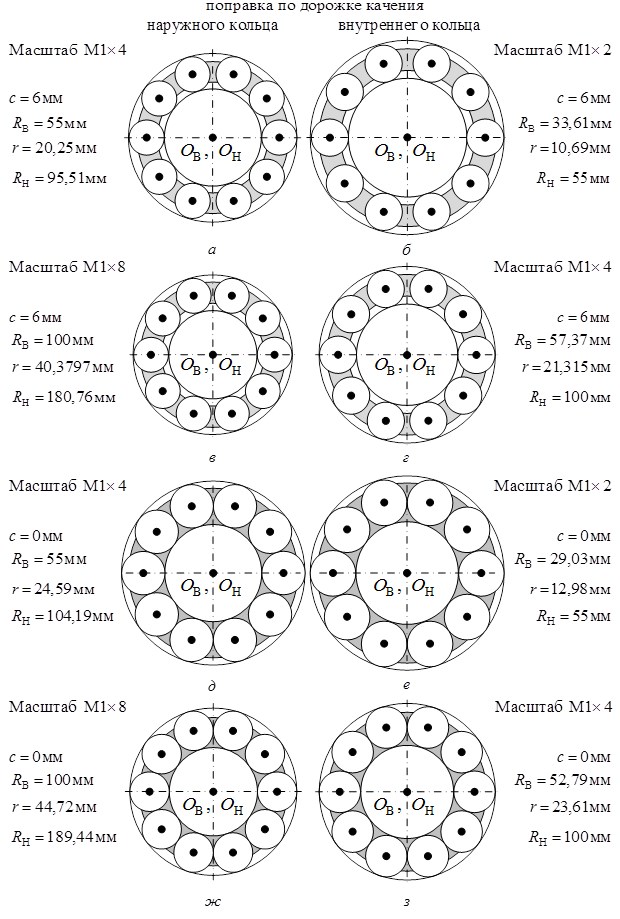
Рис. 2. Результаты компьютерного моделирования механизмов с ЗСТК с диаметрами равной величины
Анализ результатов решения задачи по определению номинальных величин геометрических параметров и компьютерного моделирования (рис. 2) механизмов с ЗСТК с диаметрами равной величины, показывает, что наличие зазора между телами качения при вводе поправки в расчет по дорожке качения наружного кольца приводит к уменьшению габаритных размеров механизма. Данное явление есть следствие снижения величин радиусов тел качения и дорожки качения наружного кольца при постоянной величине дорожки качения внутреннего кольца. В тоже время при вводе поправки в расчет по дорожке качения внутреннего кольца наличие зазора между телами качения не оказывает влияния на габаритные размеры механизма, однако приводит к уменьшению величин радиусов тел качения и к увеличению радиуса дорожки качения внутреннего кольца. Следовательно, не зависимо от направления ввода поправки в расчет номинальных значений геометрических параметров наличие зазора вызывает уменьшение радиусов тел качения, что в дальнейшем отрицательно скажется на характере качения данных звеньев и увеличит их склонность к проскальзыванию. Вариация числа тел качения в большую сторону оказывает аналогичный характер изменений. При вводе поправки в расчет геометрических параметров механизмов с ЗСТК с диаметрами равной величины по дорожке качения наружного кольца рост числа тел качения позволяет снизить величины радиусов этих звеньев и радиуса дорожки качения наружного кольца при постоянной величине радиуса дорожки качения внутреннего кольца. При вводе поправки в расчет по дорожке качения внутреннего кольца взывает рост ее радиуса при пропорциональном снижении величин радиусов тел качения не зависимо от наличия или отсутствия зазора между этими звеньями.
В результате проделанных действий получены и решены все частные случаи задачи по определению номинальных величин геометрических параметров механизмов с ЗСТК с диаметрами равной величины, что позволяет обеспечить достижение требуемых величин показателей качества механизмов приводов технологического оборудования.
Литература:
1. Мерко М. А. Кинематические и геометрические характеристики эксцентрикового механизма качения: автореф. дис. канд. техн. наук: 05.02.02. Красноярск, 2002. 26 с.
2. Мерко М. А., Меснянкин М. В., Митяев А. Е., Колотов А. В. Анализ взаимозависимостей геометрических параметров эксцентрикового механизма качения // Вестник Красноярского государственного аграрного университета. 2012. № 11. С. 180–184.
3. Меснянкин М. В., Мерко М. А., Колотов А. В., Митяев А. Е. Определение границ областей существования механизмов-прототипов эксцентрикового механизма качения при вводе поправки в расчет по дорожке качения внутреннего кольца // Вестник Красноярского государственного аграрного университета. 2012. № 12. С. 138–142.
4. Меснянкин М. В., Мерко М. А., Колотов А. В., Митяев А. Е., Белякова С. А. Определение границ областей существования механизма-прототипа ЭМК без сепаратора при вводе поправки по дорожке качения наружного кольца // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2013. Т.3. № 1. С. 33–38.
5. Мерко М. А., Меснянкин М. В., Колотов А. В. Формирование областей существования механизма с ЗСТК с диаметрами равной величины с сепаратором (водило) при вводе поправки по дорожке качения наружного кольца // Молодой ученый. 2013. № 4. С. 76–80.
6. Мерко М. А., Меснянкин М. В., Колотов А. В. Формирование областей существования механизма с ЗСТК с диаметрами равной величины с сепаратором (водило) при вводе поправки по дорожке качения внутреннего кольца // Актуальные проблемы гуманитарных и естественных наук. 2013. № 4. С.54–58.
7. Мерко М. А., Меснянкин М. В., Митяев А. Е. Зависимость областей существования механизмов с ЗСТК с диаметрами равной величины и зазора между телами качения при вводе поправкой по дорожке качения внутреннего кольца // Молодой ученый. 2013. № 5. С. 79–83.
8. Мерко М. А., Меснянкин М. В., Колотов А. В. Определение координат звеньев механизма с замкнутой системой тел качания с диаметрами равной величины // Актуальные проблемы гуманитарных и естественных наук. 2013. № 3. С.68–73.
9. Меснянкин М. В., Мерко М. А., Колотов А. В., Беляков Е. В., Белякова С. А. Математическая модель ЭМК с сепаратором при ведущем внутреннем кольце // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2012. Т.5. № 4. С. 62–67.
10. Мерко М. А., Меснянкин М. В., Митяев А. Е. Описание математической модели механизма-прототипа ЭМК с сепаратором (водило) при ведущем внутреннем кольце // Молодой ученый. 2013. № 3. С. 71–75.
11. Меснянкин М. В., Мерко М. А., Колотов А. В., Митяев А. Е. Результаты решения задачи о положениях звеньев ЭМК при ведущем внутреннем кольце // Вестник Таджикского технического университета. 2013. № 1. С. 35–41.
12. Мерко М. А., Меснянкин М. В., Колотов А. В. Передаточные отношения механизмов с ЗСТК с диаметрами равной величины и зазором при ведущем внутреннем кольце и вводе поправки по дорожке качения наружного кольца // Молодой ученый. 2013. № 6. С. 71–75.
13. Колотов А. В., Мерко М. А., Меснянкин М. В, Беляков Е. В. Автоматизированное проектирование зубчатых механизмов приводов технологического оборудования со связанными цилиндрическими колесами // Современные технологии. Системный анализ. Моделирование. 2012. № 4. С. 51–57.
14. Беляков Е. В., Колотов А. В., Мерко М. А., Меснянкин М. В. Применение САПР при исследовании эксцентрикового планетарного механизма // Современные технологии. Системный анализ. Моделирование. 2012. № 3. С. 109–112.
15. Беляков Е. В., Мерко М. А., Колотов А. В., Меснянкин М. В., Митяев А. Е. Обеспечение требуемого движения выходного звена эксцентрикового эпициклического механизма // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2012. Т.5. № 4. С. 47–51.
16. Белякова С. А., Груздев Д. Е., Беляков А. Н., Мерко М. А., Меснянкин М. В., Колотов А. В. Применение дифференциального механизма для шлифования плоских поверхностей // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2012. Т.5. № 4. С. 51–56.
17. Мерко М. А., Беляков Е. В., Колотов А. В., Меснянкин М. В., Митяев А. Е Повышение качества обработки плоских поверхностей шлифовальной машиной с эксцентриковым эпициклическим механизмом // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2013. Т. 3. № 1. С. 15–19.
18. Белякова С. А., Груздев Д. Е., Беляков А. Н., Мерко М. А., Колотов А. В., Меснянкин М. В. Применение планетарного механизма для шлифования плоских поверхностей // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2013. Т.3. № 1. С. 19–25.
19. Колотов А. В., Мерко М. А., Митяев А. Е., Беляков Е. В., Груздев Д. Е. Обеспечение условия требуемой толщины зуба при вершине для рядных цилиндрических передач методом объемного блокирующего контура // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2013. Т. 3. № 1. С. 25–33.
20. Свидетельство о государственной регистрации программы для ЭВМ № 2012614197. Программный комплекс «Эксцентрик» / Меснянкин А. В., Мерко М. А., Колотов А. В., Груздев Д. Е., Митяев А. Е., Беляков Е. В.; заявитель и правообладатель ФГАОУ ВПО «Сибирский федеральный университет»; заявка № 2012612100 от 22.03.12; зарегистрировано в Реестре программ для ЭВМ 12.05.12.
