Рассматривается задача исследования устойчивости разностных схем для численного решения уравнений колебаний прямоугольной мембраны и прямоугольной пластины. Исследование проводится методом Неймана. Выводятся соотношения зависимости шага по времени от шагов по пространственным переменным для того, чтобы использование разностной схемы приводило к решению.
Ключевые слова: прямоугольная мембрана, прямоугольная пластина, уравнение колебаний, разностная схема, устойчивость, Нейман, численное решение.
Введение. Большинство задач математической физики являются очень сложными для решения их аналитическим способом, например, задачи гашения колебаний элементов механических структур [1–14]. Поэтому огромное практическое значение имеет умение решать такие задачи численным способом, то есть аппроксимация исходной задачи конечно разностными схемами. Подобные методики дают приближённое решение, которое при увеличении точности стремится к аналитическому решению. Но чтобы такое происходило, необходимо, чтобы конечно разностные схемы были устойчивыми. Поэтому не менее значимым в вычислительной математике является нахождение условий, при которых конечно разностные схемы, полученные при аппроксимации исходной задачи, обладают условием устойчивости.
В этой работе будет показано, как найти такие условия устойчивости для численного решения уравнения колебаний прямоугольной мембраны и для численного решения уравнения колебаний прямоугольной пластины.
Исследование устойчивости конечно разностной схемы для численного решения уравнения колебаний прямоугольной мембраны. Колебания прямоугольной мембраны описываются гиперболическим уравнением
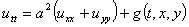 ,
, 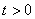 ,
,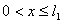 ,
,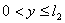 ,
,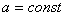 . (1)
. (1)
Начальные отклонения и скорость перемещения этого первоначального возмущения мембраны задаются так
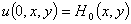 , (2)
, (2)
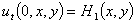 . (3)
. (3)
На границе прямоугольной мембраны наложим условие закрепления согласно
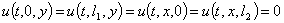 (4)
(4)
Для того чтобы численно решить систему (1) — (4), аппроксимируем её явной конечно-разностной схемой второго порядка аппроксимации. Для этого зададим натуральные числа 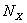 ,
, 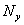 ,
, 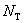 и разобьём рассматриваемую область
и разобьём рассматриваемую область 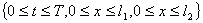 на прямоугольные ячейки параллельными прямыми
на прямоугольные ячейки параллельными прямыми
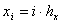 ,
, 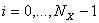 , (5)
, (5)
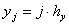 ,
, 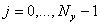 и (6)
и (6)
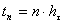 ,
, 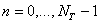 , где (7)
, где (7)
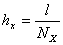 ,
, 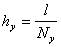 и
и 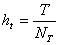 . (8)
. (8)
Конечно-разностная схема будет иметь следующий вид
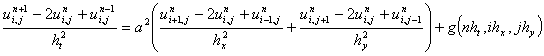 (9)
(9)
Начальное условие (1.2) и граничное условие (1.4) примут вид
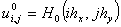 , (10)
, (10)
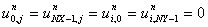 . (11)
. (11)
В силу того, что здесь ставится задача исследования устойчивости конечно разностной схемы, дальнейшие выкладки, с которыми можно ознакомиться здесь [1–14], будут опущены.
Покажем, что схема (9) устойчива. Для этого воспользуемся методом Неймана [15]: рассмотрим однородный вариант уравнения (9) и сделаем подстановку
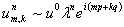 (12)
(12)
Тогда после подстановки мы получим следующее выражение
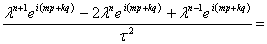
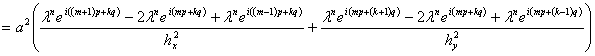 (13)
(13)
После упрощения выражение выше приводится к виду
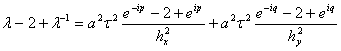 (14)
(14)
Далее раскрываем экспоненты по формуле Эйлера
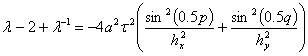 (15)
(15)
Окончательное упрощение приводит нас к квадратному уравнению
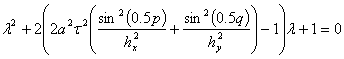 (16)
(16)
Если 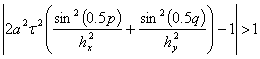 , то у нас есть 2 вещественных корня. По теореме Виета их произведение равняется 1. Следовательно, значение одного из них меньше единицы, а значение другого — больше. Этот случай нас не устраивает. Если
, то у нас есть 2 вещественных корня. По теореме Виета их произведение равняется 1. Следовательно, значение одного из них меньше единицы, а значение другого — больше. Этот случай нас не устраивает. Если
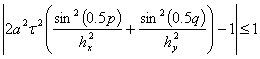 , (17)
, (17)
тогда 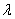 — комплексные и, следовательно,
— комплексные и, следовательно, 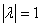 . Этот случай нам подходит. Из (17) следует, что
. Этот случай нам подходит. Из (17) следует, что
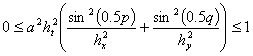 (18)
(18)
Тогда
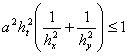 , (19)
, (19)
И значит
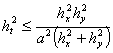 (20)
(20)
Поэтому схема (9) устойчива, если шаг по времени 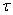 удовлетворяет (условная устойчивость) неравенству
удовлетворяет (условная устойчивость) неравенству
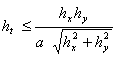 (21)
(21)
Приведём пример использования конечно разностной схемы (9). В примере задавались входные параметры 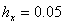 ,
, 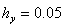 ,
, 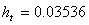 ,
, 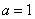 ,
, 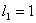 ,
, 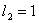 . Графики значений функции
. Графики значений функции 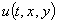 строились в сечении
строились в сечении 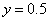 .
.
Пример 1. Рассматривается задача о свободном колебании прямоугольной мембраны с начальными условиями 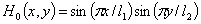 ,
, 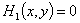 ,
, 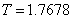 или 50 точек по времени. На рис. 1 изображено поведение свободных колебаний прямоугольной мембраны, то есть вид функции
или 50 точек по времени. На рис. 1 изображено поведение свободных колебаний прямоугольной мембраны, то есть вид функции 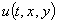
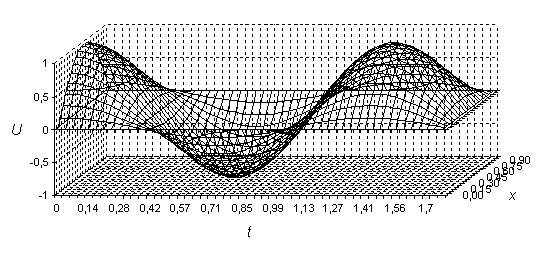
Рис. 1. Процесс колебания в сечении y0=0.5
Исследование устойчивости конечно разностной схемы для численного решения уравнения колебаний прямоугольной пластины. Малые поперечные колебания упругой изотропной пластины постоянной толщины описываются уравнением Жармен-Лагранжа
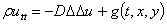 ,
, 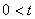 ,
,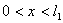 ,
, 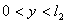 (22)
(22)
Здесь 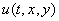 - поперечный прогиб срединной плоскости пластины;
- поперечный прогиб срединной плоскости пластины; 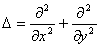 — двумерный оператор Лапласа;
— двумерный оператор Лапласа; 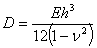 — изгибная жесткость пластинки;
— изгибная жесткость пластинки; 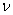 — коэффициент Пуассона;
— коэффициент Пуассона; 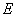 — модуль Юнга;
— модуль Юнга; 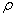 — удельная плотность на единицу площади пластинки;
— удельная плотность на единицу площади пластинки; 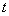 — время.
— время.
Начальные отклонение и скорость его распространения будем рассматривать как начальные условия
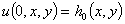 ,
, 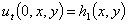 . (23)
. (23)
На концах пластины наложим условия шарнирного закрепления
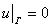
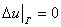 (24)
(24)
Для удобства перепишем уравнение следующим образом
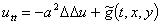 ,
, 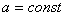 (25)
(25)
Для того чтобы численно решить задачу (22) — (25), представим её в виде системы уравнений
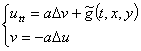 , (26)
, (26)
Для того чтобы численно решить систему (26), построим разностную схему для приближённого решения системы [15]. Зададим натуральные числа 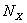 и
и 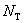 , и разобьём рассматриваемую область
, и разобьём рассматриваемую область 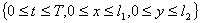 на прямоугольные ячейки параллельными прямыми
на прямоугольные ячейки параллельными прямыми 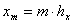 ,
, 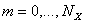 ,
, 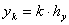 ,
, 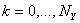 ,
, 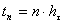 ,
, 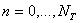 , где
, где 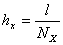 ,
, 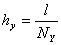 и
и 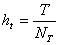 . В результате этих операций мы можем записать следующее
. В результате этих операций мы можем записать следующее
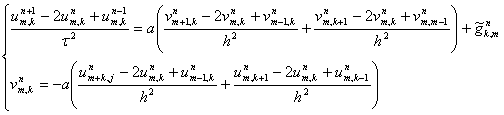 (27)
(27)
Теперь нам необходимо проверить является ли разностная схема (27) устойчивой. Для этого можно воспользоваться спектральным признаком устойчивости Неймана [15]. Рассмотрим однородное уравнение (3.143), тогда у нас получится, что
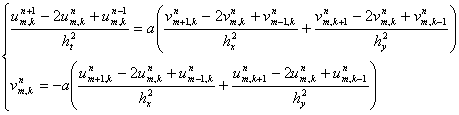 (28)
(28)
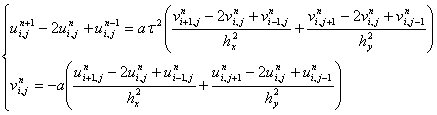 (29)
(29)
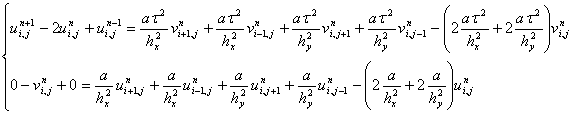 (30)
(30)
Согласно спектральному признаку устойчивости Неймана [15] зададим следующее значение
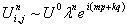 , (31)
, (31)
которое подставим в (30). Получим следующее выражение
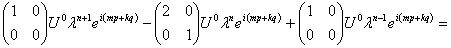
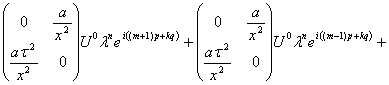
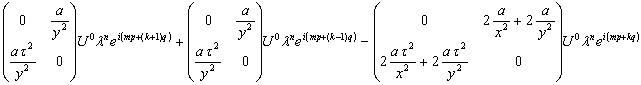
(32)
Введём следующие обозначения для матриц, записанных в (32)
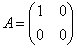 ,
, 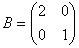 ,
, 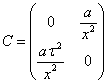 (33)
(33)
Подставив эти обозначения в (32), получим следующую запись для этого выражения
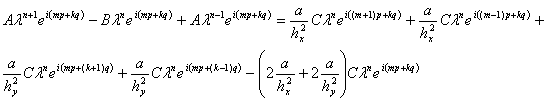 (34)
(34)
Разделим выражение (34) на значение 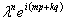 , получим
, получим
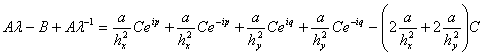 (35)
(35)
Соберём все подобные слагаемые, тогда будет
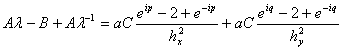 (36)
(36)
Применим формулу Эйлера и вспомним тригонометрические равенства
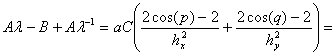
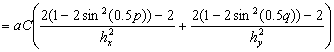 (37)
(37)
Ещё раз группируем в более удобный вид
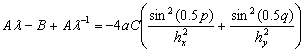 (38)
(38)
И получаем квадратное уравнение
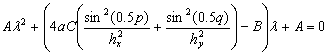 (39)
(39)
Вспоминаем истинные значения матриц (33)
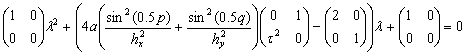 (40)
(40)
Попробуем упростить
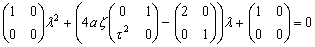 (41)
(41)
Ещё одна итерация группировки
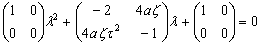 (42)
(42)
В результате получаем удобную запись
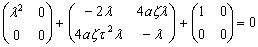 (43)
(43)
От куда у нас получается, что
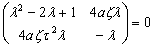 (44)
(44)
Чтобы эта система имела решение, необходимо и достаточно, чтобы её детерминант равнялся 0
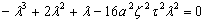 (45)
(45)
Тогда у нас получится
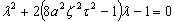 (46)
(46)
Воспользуемся правилом Виета
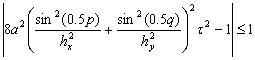 (47)
(47)
От куда получается, что
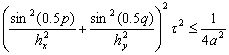 (48)
(48)
Окончательно имеем следующую оценку
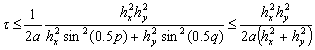 (49)
(49)
Из выражения (49) можно заключить, что схема (27) является условно устойчивой.
Приведём примеры использования конечно разностной схемы (27). В приведённом ниже примере задавались входные параметры 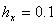 ,
, 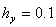 ,
, 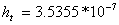 ,
, 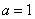 ,
, 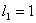 ,
, 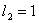 . Графики значений функции
. Графики значений функции 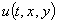 строились в сечении
строились в сечении 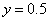 .
.
Пример 2. Рассматривается задача о свободном колебании прямоугольной пластины с начальными условиями 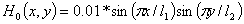 ,
, 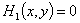 ,
, 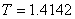 или 4000 точек по времени. На рис. 2 изображено поведение свободных колебаний прямоугольной пластины, то есть вид функции
или 4000 точек по времени. На рис. 2 изображено поведение свободных колебаний прямоугольной пластины, то есть вид функции 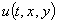
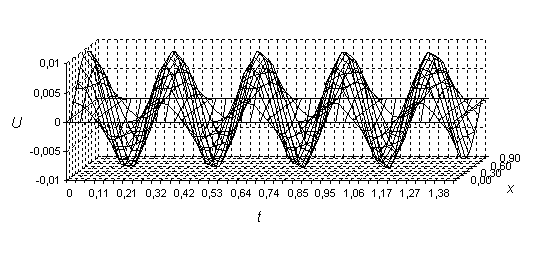
Рис. 2. Процесс колебания прямоугольной пластины
Литература:
1. Атамуратов А. Ж., Михайлов И. Е., Муравей Л. А.. О гашении колебаний балки. // Труды ИСА РАН. Динамика неоднородных систем. Том 50(1). — М.: Книжный дом «ЛИБРОКОМ», 2010. — С. 53–58.
2. Атамуратов А. Ж., Михайлов И. Е., Муравей Л. А. О гашении колебаний сложных механических структур // Авиакосмическая техника и технология, 2012, № 4. С. 54–59.
3. Атамуратов А. Ж. О гашении колебаний прямоугольной мембраны // Вестник Тверского государственного университета. Серия Прикладная математика. — 2013. — № 2. — С. 49–59.
4. Атамуратов А. Ж. Исследование подходов к решению задач математической физики на примере уравнения колебаний прямоугольной мембраны // Молодой ученый. № 10. 2013. С. 1–5. http://www.moluch.ru/archive/57/6198/
5. Атамуратов А. Ж. Приведение к тригонометрической проблеме моментов на примере задачи гашения колебаний прямоугольной мембраны, балки и прямоугольной пластины // Молодой ученый. № 11. 2013. С. 6–10. http://www.moluch.ru/archive/58/8092/
6. Атамуратов А. Ж. Получение интегралов энергии для прямоугольной мембраны, балки и прямоугольной пластины // Молодой ученый. № 11. 2013. С. 10–15. http://www.moluch.ru/archive/58/8112/
7. Атамуратов А. Ж., Михайлов И. Е. Численное решение задачи о гашении колебаний балки. Тезисы докладов Международной конференции по прикладной математике и информатике, посвященной 100-летию со дня рождения академика А. А. Дородницына. ВЦ РАН, Москва, 7–11 декабря 2010 г. С. 83–84.
8. Muravey L., Mikhailov I., Atamuratov A., The damping problem of vibrations for large mechanical systems // ICIAM2011, Abstracts, Vancouver, Canada, July 18–22, 2011. P. 87.
9. Atamuratov A., Mikhailov I., Muravey L. On the numerical damping of beam’s vibrations // VII International Aerospace Congress IAC’12. Abstracts. Moscow, Russia. 26–31 August, 2012. P. 31–32.
10. Атамуратов А. Ж. Решение уравнения колебаний балки. // XXXV ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции. Москва, апрель 2008 г. Москва: МАТИ, 2008. Т.5.
11. Атамуратов А. Ж. О гашении колебаний балки. // XXXVI ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции. Москва, апрель 2010 г. Москва: МАТИ, 2010. Т.5.
12. Атамуратов А. Ж. О гашении колебаний прямоугольной мембраны. // XXXVII ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции в 8 томах. Москва, 5–8 апреля 2011 г. Москва: МАТИ, 2011. Т.5, С. 60–61
13. Атамуратов А. Ж. Решение уравнения колебаний круглой пластины. // XXXVIII ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции в 8 томах. Москва, 10–14 апреля 2012 г. Москва: МАТИ, 2012. Т.5, С. 38–39
14. Атамуратов А. Ж. Численный метод решения колебаний прямоугольной пластины. // XXXIX ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференций в 9 томах. Москва, 9–13 апреля 2013 г. Москва: МАТИ, 2013. Т.5, С. 32–33
15. Самарский А. А., Гулин А. В. Численные методы. Москва: Наука, 1989. 432 с.

