- Программа по математике средней общеобразовательной
школы в явном виде не упоминает о содержательно-методической
линии «Задачи с параметрами», однако упомянутая
линия присутствует в школьном курсе математики, а также
является неотъемлемым компонентом ГИА (задание части 2) и ЕГЭ
(уровень С5).
- Анализ результатов сдачи ГИА и ЕГЭ, относительно содержательно-методической линии «Задачи с параметрами» позволяет нам сделать следующие выводы о том, что [2]:
- экзаменуемые неспособны математически грамотно и ясно записать решение соответствующих задач, проводить необходимые пояснения и обоснования;
- экзаменуемые с трудом справляются с заданиями, в которых необходимо применить хорошо известный им алгоритм в чуть изменившейся ситуации (именно это и является характерным признаком задач с параметрами);
- экзаменуемые не умеют проводить доказательные рассуждения при решении рассматриваемых задач (в особенности, при решении квадратных уравнений и неравенств с параметром), выстраивать аргументацию при доказательстве известных фактов, записывать математические рассуждения, доказательства.
- Цель данной статьи — представление
анализа школьных программ по алгебре 7–9 классов
и установление соответствия между значимостью изучения
содержательно-методической линии «Задачи с параметрами»
и конкретным учебным временем отводимым на изучение названной
линии.
- Итак, открывая учебники алгебры для учащихся 7, 8, 9 классов общеобразовательных учреждений (базовый уровень) под редакцией Мордковича А. Г. мы не увидим ни одного параграфа имеющего название: «Задачи с параметрами» или «Уравнения и неравенства с параметрами». Само же понятие «параметр» и «уравнение с параметром» приведено в учебнике алгебры за 8 класс в главе 4 «Квадратные уравнения» в § 25 «Формулы корней квадратных уравнений» в таком виде [6]:
- «Решить уравнение
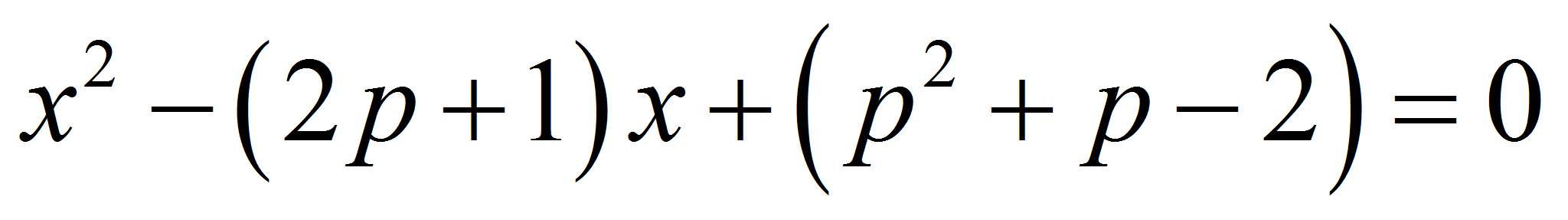.- Это квадратное уравнение отличается от всех рассмотренных до сих пор квадратных уравнений тем, что в роли коэффициентов выступают не конкретные числа, а буквенные выражения. Такие уравнения названы уравнениями с буквенными коэффициентами или уравнениями с параметрами».
- В тексте параграфа разобраны 2 примера на решение уравнений с параметром. В задачнике к § 25 «Формулы корней квадратных уравнений» представлено 48 заданий, 5 из которых посвящены уравнениям с параметром. Далее мы встречаем разбор одного примера с параметром в главе 5 «Неравенства» в § 34 «Решение квадратных неравенств» в котором требуется определить количество корней в зависимости от значений параметра. В задачнике к § 34 «Решение квадратных неравенств» представлено 46 заданий в 8 из которых представлены неравенства параметром [7].
- В учебниках алгебры для учащихся 7 и 9 классов (базовый уровень) под редакцией Мордковича А. Г. уравнения и неравенства с параметром не представлены.
- Часов отводимых на изучение содержательно-методической линии «Задачи с параметрами» в учебной программе не прописано, т. е. данные задачи если и включены в какие-либо темы, то с пометкой «повышенной сложности» и на уроках алгебры чаще всего не рассматриваются.
- Проанализируем далее учебники алгебры для учащихся 7–9 классов под редакцией Мордковича А. Г. профильного уровня. Здесь содержательно-методической линии «Задачи с параметрами» безусловно присутствует в явном виде как и часы отводимые на ее изучение.
- В учебнике для учащихся 8 класса с повышенным уровнем математической подготовки в общеобразовательных школах в главе 6 «Алгебраические уравнения» § 39 имеет название «Задачи с параметрами», число часов отводимое на его изучение равняется 6 [10]. В тексте параграфа разобрано 5 примеров и приведены замечания, также дано определение параметра. «Если дано уравнение f(x, a) = 0, которое надо решить относительно переменной х и в котором буквой а обозначено произвольное действительное число, то говорят, что задано уравнение с параметром» [8]. В задачнике представлено 83 задания к этому параграфу [4].
- В учебнике для 9 класса с повышенным уровнем математической подготовки в общеобразовательных школах Мордковича А. Г. в главе 1 «Неравенства с одной переменной. Системы и совокупности неравенств» § 7 также имеет название «Задачи с параметрами» [9], число часов отводимое на изучение равняется 6 [10]. В тексте параграфа разобрано 3 примера.
- Пример 1 — на количество корней квадратного уравнения в зависимости от параметра; пример 2 — представляет уравнение с параметром и модулем; пример 3 — система неравенств с параметром. В задачнике представлено 76 заданий к этому параграфу [3].
- В учебниках алгебры за 7 класс и 9 класс с повышенным уровнем математической подготовки в общеобразовательных школах Мордковича А. Г. задачи с параметром не представлены.
- Что касается учебников алгебры под редакцией Теляковского С. А. (базовый уровень, 7 класс), то мы не увидели никакой теории по задачам с параметрами, сами же задания на уравнения с параметром в учебнике присутствуют, но отмечены как «трудная задача». Число заданий с параметрами составляет 5 % от общего числа задач учебника.
- В учебнике 8 классе, названного автора, присутствует пункт 27 «Уравнения с параметром» с пометкой вначале пункта «Для тех, кто хочет знать больше», т. е. данный пункт не разбирается на уроках алгебры в классе. Здесь приведено 2 примера на решение уравнений с параметром [1].
- В учебнике 9 класса дело обстоит также как и в учебнике за 7 класс.
- Итак, нами установлено, что содержательно-методической линии «Задачи с параметрами» и часы отводимые на ее изучение присутствуют только в учебниках алгебры профильного уровня, во всех остальных же учебниках уравнения и неравенства с параметрами находится в разделе «трудных задач» или «задач повышенной сложности», что приводит к «обеднению» школьного курса алгебры.
- Отметим, что задачи с параметрами (в частности уравнения и неравенства с параметрами) обладают большим потенциалом в развитии исследовательских умений таких, как умение наблюдать, анализировать, выдвигать и доказывать гипотезу, обобщать и др. Данные задачи играют важную роль в формировании логического мышления и математической культуры как у школьников, так и у студентов.
- Проанализировав диссертационные исследования, учебные пособия и программы (посвященные задачам с параметрами), а также государственные образовательные стандарты отметим следующее [5]:
- Во-первых, задачи с параметрами полностью отсутствуют в учебных программах основной средней школы.
- Во-вторых, задачи с параметрами являются наиболее сложными в техническом плане (как с позиции школьников, так и с позиции учителей математики).
- В-третьих, овладение школьниками методами решения задачи с параметрами ведет к более глубокому пониманию всего школьного курса математики.
- В-четвертых, благодаря своей высокой диагностической и прогностической ценности задачи с параметрами:
- Итак, открывая учебники алгебры для учащихся 7, 8, 9 классов общеобразовательных учреждений (базовый уровень) под редакцией Мордковича А. Г. мы не увидим ни одного параграфа имеющего название: «Задачи с параметрами» или «Уравнения и неравенства с параметрами». Само же понятие «параметр» и «уравнение с параметром» приведено в учебнике алгебры за 8 класс в главе 4 «Квадратные уравнения» в § 25 «Формулы корней квадратных уравнений» в таком виде [6]:
- развивают у учащихся логическое мышление;
- формируют математическую культуру учащихся;
- помогают учащимся в овладении техники исследования;
- позволяют учителю выявить нестандартность мышления учащегося;
- наталкивают учащихся проводить элементарные математические рассуждения;
- открывают перед учащимися значительное число эвристических приемов.
- Задачи с параметрами позволяют сформировать ключевые компетенции, применимые как в учебной, так и в будущей профессиональной деятельности:
- использование приобретенных знаний и умений в практической деятельности и повседневной жизни;
- проведение анализа ситуаций;
- планирование своей деятельности;
- осуществление самоконтроля;
- планирование и выбор более рационального решения;
- работа с учебной и научной литературой;
- систематизация знания по теме, решение и составление аналогичных задачи и др.
- Целенаправленное использование задач с параметрами позволяет развивать и диагностировать развитие ряда предметных компетенций учащихся.
- Выполнять вычисления и преобразования.
- Решать уравнения и неравенства, в том числе:
- находить область допустимых значений;
- приводить дроби к общему знаменателю;
- приводить подобные слагаемые;
- производить проверку принадлежности корней уравнения области допустимых значений;
- применять метод группировки слагаемых;
- свободно владеть формулами сокращенного умножения и др.
- Выполнять действия с функциями.
- Выполнять действия с геометрическими фигурами, координатами и векторами.
- Строить и исследовать простейшие математические модели.
- К сожалению, на сегодняшний день, подготовить даже
очень сильных учащихся к выполнению задач с параметрами
в условиях базовой школы не представляется возможным. Для этого
необходим акцент на развитие вариативности математического
образования, серьезная кружковая, факультативная и т. п.
работа под руководством специально
подготовленных преподавателей [2].
- Литература:
- Алгебра: учеб. для 8 кл. общеобразоват. учреждений / под ред. С. А. Теляковского. — М.: Просвещение, 2007. — 271 с.
- Аналитический отчет предметной комиссии о результатах государственной (итоговой) аттестации выпускников 9 классов по математике / Н. А. Зорина, Л. А. Жигулев — СПб.: СПбАППО, 2012. — 19 с.
- Звавич Л. И. Алгебра. 9 класс: задачник для учащихся общеобразоват. учреждений / Л. И. Звавич, А. Р. Рязановский, П. В. Семенов. — М.: Мнемозина, 2008. — 336 с.
- Звавич Л. И. Алгебра. 8 класс: задачник для учащихся общеобразоват. учреждений / Л. И. Звавич, А. Р. Рязановский. — М.: Мнемозина, 2008. — 271 с.
- Качалова Г. А. О необходимости включения содержательно-методической линии «Задачи с параметрами» в учебный модуль «Основы математики» // Materiały Międzynarodowej Naukowi-Praktycznej konferencji Postępów w nauce. Nowe poglądy, problemy, innowacje. 29.07.2012. — 31.07.2012. Część 2. — Łódź, 2012. — С. 67–70.
- Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — М.: Мнемозина, 2009. — 215 с.
- Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. — М.: Мнемозина, 2009. — 255 с.
- Мордкович А. Г. Алгебра. 8 класс: учеб. для учащихся общеобразоват. учреждений / А. Г. Мордкович, Н. П. Николаев. — М.: Мнемозина, 2008. — 240 с.
- Мордкович А. Г. Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений / А. Г. Мордкович, Н. П. Николаев. —М.: Мнемозина, 2008. — 255 с.
- Программы. Математика. 5–6 классы. Алгебра. 7–9 классы. Алгебра и начала математического анализа. 10–11 классы. / авт.-сост. И. И. Зубарева, А. Г. Мордкович. — М.: Мнемозина, 2009. — 63 с.