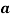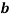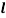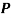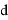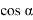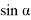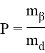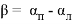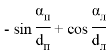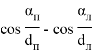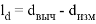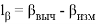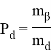О точности комбинированной засечки



В данной статье рассматриваются результаты оценки точности способа «свободная станция». Также приведены теоретически — практические исследования по решению задачи — установки средней квадратической погрешности для данного способа.

Ключевые слова: координаты, погрешность.

При выполнении геодезических работ в населенных пунктах, строительных площадках широкое применение, для определения координат исходной геодезической основы, нашел способ «свободная станция». Тахеометр устанавливается в любой точке, так чтобы была возможность измерить горизонтальные углы и и расстояния , и (см. рис. 1).

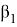
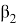
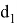
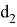
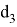
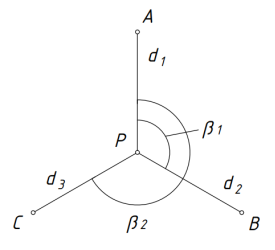
Рис. 1. Схема расположения пунктов

В качестве исходных пунктов принимаются стенные знаки — марки, закрепленные в стенках зданий на высоте от земли 0,6–0,8 м, или на строительной площадке — специальные поворотные знаки [1] на высоте 2–10 м.

По результатам измерений вычисляют координаты x, y пункта Р. Для решения этой задачи обычно применяют параметрический способ уравнивания [2]. В этом способе уравнивания, неизвестное (параметр) представляют в виде суммы двух слагаемых: приближенного значения координат точки и поправки

(1)

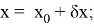
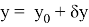
Приближенные значения , — вычисляют по формулам обратной засечки, используя измеренные углы, или по формулам линейной засечки.

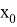
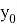
Уравнения поправок в параметрическом способе уравнивания имеют вид

(2)

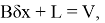
где — матрица коэффициентов уравнений поправок; — матрица поправок к приближенным значениям координат определяемого пункта; — матрица свободных членов; — матрица поправок к результатам измерений.

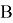
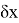
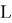
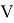
Элементы матрицы — частные производные от измеренных величин и . Обобщенные формулы для вычисления элементов матрицы поправок приведены в табл. 1.

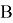
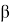
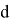
Коэффициенты уравнений поправок

Таблица 1

Виды измерений
Расстояния
Углы (П — правое направление, Л — левое направление)
Свободные члены: сторон, углов
Веса сторон, углов				1

Используя коэффициенты уравнения поправок (табл. 1) составляют систему нормальных уравнений

(3)

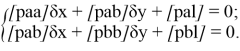
Из решения системы нормальных уравнений вычисляют поправки и , и по формуле (1) получают точные значения координат пункта Р.

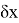
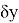
Для вычисления средней квадратичной погрешности (СКП) положения точки Р нужно определить обратную матрицу уравненных неизвестных

(4)

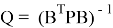
С ее помощью находят СКП координат точки Р по формулам

(5)

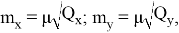
где среднюю квадратическую погрешность единицы веса вычисляют по формуле

(6)

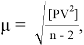
где — число всех измерений.

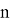
Общая погрешность определения координат точки (пункта) Р равна

(7)

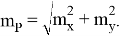
Из изложенного материала следует, что уравнение построения — вычисление координат и СКП положения точки представляет достаточно большой объем работы.

Как установлено [3], ошибка в положении точки Р зависит от конфигурации треугольника АВС, и расположения точки относительно исходных пунктов А, В, С.

Таким образом, при неудачном выборе положения искомой точки, может получится значительная погрешность определения её координат, превышающая допустимое значение. В таком случае, нужно выбрать другое положение точки и вновь выполнить уравнивание. Поэтому, представляет практический интерес и необходимость, по предварительно определенному положению точки на местности, установить её СКП.

Для решения этой задачи, выполнены теоретически — практические исследования:

– составлена модель геодезической сети;

– выполнено уравнивание с разными исходными данными;

– результаты исследований, для применения в практике, представлены в виде графика — номограммы.

В качестве модели сети принят полигонометрический ход (линия В — А — С) с длиной сторон ВА = АС = СВ = 200 м. В сети пункты А, В, С являются исходными, а пункт К — центральная точка, точка Р — определяемая (рис. 2).

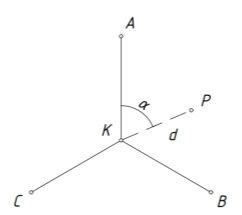
Рис. 2. Схема исследуемой сети

Используя параметрический способ уравнивания, приняв угол и расстояние = 20 и 120 м., вычислили СКП точки Р.

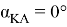
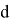
Далее последовательно принимали угол и расстояния 20 и 120 м по каждому направлению, вычисляли СКП точки Р.

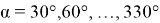
Результаты вычислений свели в таблицу и для практического применения представили в виде графика — номограммы (рис. 3).

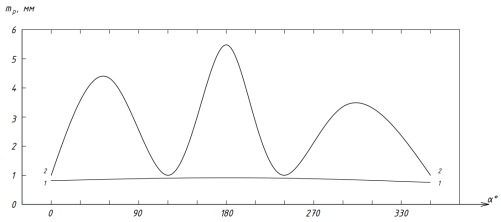
Рис. 3. График зависимости СКП от угла и расстояния

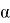
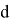
На графике по x отложены значения углов , по оси y — значение СКП точки.

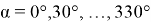
На рис. 3 кривая 1–1 представляет значение СКП точек для расстояния = 20 м., а кривая 2–2 — = 120 м. Определение СКП погрешности положения точки Р осуществляется в таком порядке, например, = 0, = 50 м., вычисляется отношение м = 50/120 м, строим это отношение от точки 1 к точке 2 и от полученной точки строим перпендикуляр на ось y, с которой снимаем показание СКП положения определяемой точки Р, полученную величину (мм) следует умножить на СКП измерения угла, т. е. в конечном счете ошибка положения точки определяется кроме геометрии построения, средней квадратической погрешностью измерения угла. При определении погрешности положения точки не учитываются погрешности исходных данных.

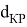
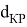
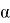
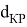
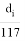
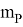
Литература:

1. Колмаков Ю. А., Дронь О. Е. Точность определения координат геодезического пункта способом «свободная станция». // Вузовская наука в современных условиях: сборник материалов 48-й НТК (январь 2014 год). Ульяновск: УлГТУ, 2014–230 с. — с. 191–194.
2. Брынь М. Я., Лобанова Ю. В., Афонин Д. А., Шевченко Г. Г. Оценка точности определения положения точек способом свободного станционирования. // Геодезия и картография. — 2021. — № 5. — с. 2–9.
3. Колмаков Ю. А., Перкакуев Н. Ю. О точности комбинированной засечки. // Вузовская наука в современных условиях: сборник материалов 55-й НТК (25–30 января 2021 года). В 3 ч. ч. 2. — Ульяновск: УлГТУ, 2021–276 с. — с. 41–44.