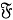Рассматриваются только конечные группы. Пусть
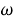
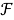

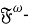



Ключевые слова:
группа, конечная группа, множество Фиттинга группы, нормальная подгруппа,
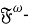
Рассматриваются только конечные группы. В современной теории групп большое внимание уделяется вопросам изучения подгрупп, определяемых посредством заданного класса групп
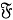
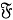
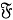
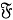
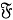
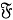
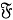
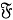
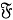

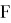
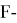
В работе [1] в качестве естественного обобщения понятия
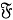
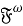
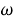
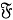
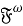
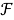

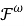

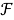

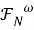


В работе используется терминология, принятая в книгах [3, 11]. Запись
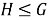
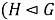
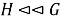
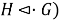
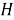

Определение 1.
Непустое множество
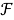


(1) из
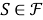
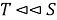
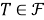
(2) из
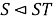
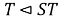
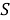
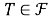
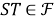
(3) из
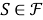
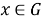
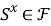
Определение 2.
Пусть
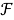

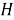

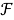

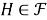
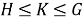
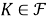
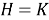
Определение 3.
Пусть
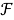

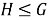
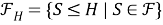
Замечание 1.
Если
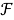

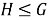
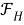
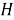
Определение 4
. Пусть

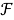

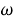
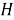

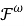

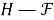

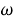
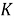

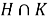
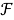
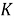
Замечание 2.
Пусть

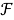

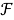

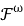
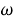
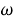
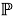
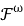
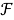
Теорема 1.
Пусть

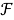

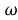
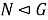
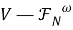

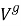
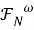

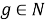
Доказательство.
Пусть

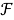

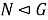
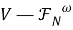

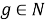
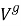
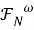

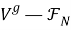

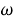
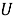

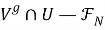
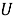
-
Установим, что
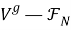

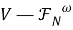

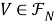
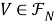
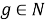
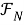

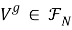
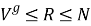
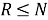
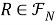
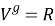
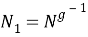
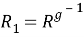
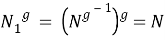
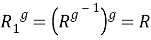
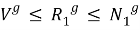
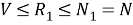
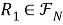
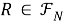
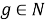
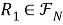
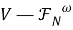

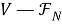

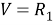
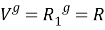
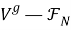

-
Пусть
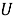
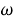

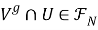
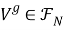
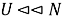
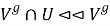
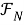

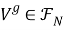
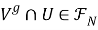
-
Покажем, что пересечение
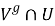
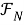
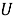
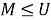
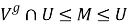
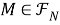
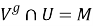
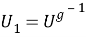
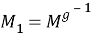
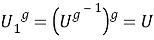
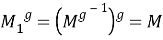
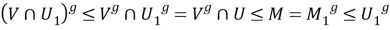
Следовательно,
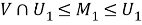
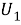
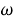

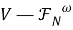

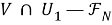
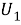
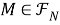
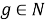
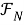

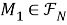
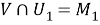
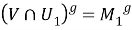
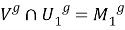
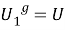
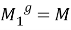
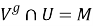
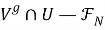
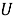
Из 1) — 3) следует, что
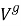
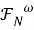

Следствие 1
[11, (VIII.2.7.)]. Пусть

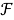

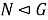
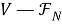

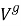
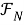

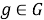
Литература:
-
Ведерников, В.А.
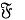
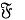
- Воробьев, Н. Т. Множества Хартли и инъекторы конечной группы / Н. Т. Воробьев, Т. Б. Караулова // Математические заметки. — 2019. — Т. 105, № 2. — С. 214–227.
- Монахов, В. С. Введение в теорию конечных групп и их классов / В. С. Монахов. — Мн.: Выш. шк., 2006. — 207 c.
- Новикова, Д. Г. О множествах Фиттинга и инъекторах конечных групп / Д. Г. Новикова, М. М. Сорокина // Материалы Международной научно-практической конференции «Теоретические и прикладные аспекты естественнонаучного образования в эпоху цифровизации». — Брянск: БГУ им. И. Г. Петровского, 2023. — С. 82–86.
- Путилов, С. В. Классы групп / С. В. Путилов, М. М. Сорокина. — Брянск: Белобережье, 2018. — 100 c.
- Семенов, М. Г. Инъекторы во множестве Фиттинга конечной группы / М. Г. Семенов, Н. Т. Воробьев // Математические заметки. — 2015. — Т. 97, № 4. — С. 516–528.
-
Сорокина М. М. О
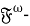
- Anderson, W. Fitting Sets in Finite Soluble Groups / W. Anderson // Ph. D. thesis. — Michigan State University. — 1973. — 270 p.
- Anderson, W. Injector in Finite Solvable Groups / W. Anderson // J. Algebra. –1975. — Vol. 36, № 3. — P. 333–338.
- Ballester-Bolinches, A. Classes of Finite Groups / A. Ballester-Bolinches, L. M. Ezquerro. — Dordrecht: Springer, 2006. — 381 p.
- Doerk, K. Finite Soluble Groups / K. Doerk, T. Нawkes. — Berlin — New York: Walter de Gruyter, 1992. — 891 p.
- Fischer, B. Injectoren Endlicher Auflosbarer Cruppen / B. Fischer, W. Gaschutz, B. Hartley // Math. Z. — 1967. — Vol. 102, № 5. — P. 337–339.
- Guo, W. The Theory of Classes of Groups / W. Guo. — Beijing — New York: Science Press, 2000. — 251 p.
-
Yang, N. On