Статья посвящена вопросам моделирования железобетонных балок прямоугольного сечения с одиночной рабочей арматурой под действием статической нагрузки. Рассмотрены принципы и критерии подобия при моделировании строительных конструкций, в частности железобетонных балок. На основе анализа дифференциального уравнения изогнтой оси балки найдены масштабные коэффициенты действующей нагрузки, изгибающего момента и прогиба в середине балки. Изложены сопоставительные анализы полученных коэффициентов подобий и численного моделирования с использованием программного комплекса ЛИРА-САПР 2017. Приведены технико-экономические сравнения затрат на изготовление 3-х моделей и 3-х натурных балок.
Ключевые слова: железобетонная балка, модельная конструкция, уравнение изогнутой оси балки, коэффициент подобия, эксперимент, напряжённое состояние, численное моделирование, натурная конструкция.
The article is devoted to the modeling of reinforced concrete beams of rectangular cross-section with a single working armature under the action of static load. The principles and criteria of similarity in the modeling of building structures, in particular, reinforced concrete beams, are considered. Based on the analysis of the differential equation of the curved axis of the beam and the similarity criteria, the scale coefficients of the acting load, bending moment and deflection in the middle of the beam are found. Comparative analyses of the obtained similarity coefficients in the analysis of equations and numerical modeling using the LIRA-CAD 2017 software package are presented. Technical and economic comparisons of the costs of manufacturing 3 models and 3 full-scale beams are given.
Keywords: reinforced concrete beam, model structure, beam curved axis equation, similarity coefficient, experiment, stress state, numerical simulation, full-scale structure.
Целью изучения реальных объектов на моделях состоит в том, что с использованием теории подобия перенести количественные результаты на подобные натурные объекты. Однако вопросы наиболее точного физического и геометрического моделирования, а также подобия не до конца исследованы и эти задачи сегодня становятся наиболее актуальными [1]. В последние годы экспериментальные исследования строительных конструкций проводятся в возрастающем объеме, и вопросы наиболее точного моделирования и подобия остро встают перед исследователями. Каждый эксперимент проводится для проверки каких-либо теоретических положений и дальнейшего распространения, и внедрения результатов, полученных при проведении опыта, на реальные объекты. Любой опыт, проводимый в лаборатории на моделях, основывается на двух главных категориях подобия: «константе подобия» и «уравнения связи» [2]. Константа подобия — постоянное число, выражающее отношение одноименных величин в соответствующих точках геометрически подобных систем. Количество величин, входящих в константу подобия, может быть различным. Отношения между подобными объектами обусловлено определенными физическими законами или «связями». Следовательно, константы подобия не могут быть выбраны произвольно, а должны быть получены из «уравнений связи», т. е. из математических выражений физических законов.
При экспериментальном методе изучения прочностных характеристик конструкций в основе исследования, как правило, лежит «критерий механического подобия». Многие методы структурного моделирования основаны на вышеуказанных критериях. Часто размеры экспериментальной модели задаются лишь из условия геометрического подобия, а вместо силового подобия ставится условие равенства напряженных состояний модели и натурной конструкции. Методы нелинейного физического моделирования до конца не разработаны, как правило, в ходе экспериментов окончательный вывод о работоспособности натурной конструкции делают не по упругой стадии, а по стадии разрушения экспериментальной модели. В этом случае исследование конструкции в предельном состоянии методами линейного моделирования дает лишь приближённый результат. Тогда константы подобия выводятся из уравнений связи, линейно выражающих зависимость напряженного состояния модели и натурной конструкции.
В работе [3] изложен вопрос распространение механических возмущений в подобных телах. Рассматривается простейший случай подобные тела
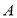
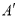
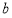
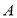
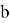
Материалы и методика испытания кубов на осевое сжатие и железобетонных балок на изгиб
Кубики с длиной ребра 100 мм, призмы размером 100х100х400мм были изготовлены из того же бетона, как балки прямоугольного сечения. Изготовленные стандартные образцы из бетона испытывались на сжатие, в результате которых определялись физические характеристики [10].
Значения физических и геометрических характеристик кубов приведены в табл. 1.
Таблица 1
Определение класс бетона
|
№ |
Масса (гр) |
Размеры кубика (мм) |
Разрушающая нагрузка |
Средняя раз. нагрузка |
Средняя прочность (α=0,95) |
Класс бетона |
|
1 |
2315 |
100х100х100 |
21833 кг |
21389 кг |
|
B15 |
|
2 |
2316 |
100х100х100 |
20167 кг | |||
|
3 |
2361 |
100х100х100 |
22167 кг |
Испытание кубов производилось после 28 суток с момента их изготовления на гидравлическом прессе Р-50. В соответствии с требованием [10–13] были проведены выравнивание поверхности формы кубов. Образцы кубиков представлены на рис.1, а. По результату испытания кубов определяли класс бетона изготовленной модели железобетонной балки. Нагрузка на кубике увеличивалась со скоростью, обеспечивающей разрушения образца после 30–60 с момента испытаний. Характер разрушения бетонных кубиков и призм представлены на рис. 1, б,в.

Рис. 1. Образцы и характер разрушения бетонных кубиков и призм
Прежде чем приступить к испытанию модели железобетонной балки и исследования его напряжённо-деформированного состояния также были проведены испытания арматуры на разрыв по ГОСТ 34028–2016 [9]. Эти испытания проводились для получения диаграммы
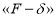

Рис. 2. Испытание образцов арматуры на растяжение
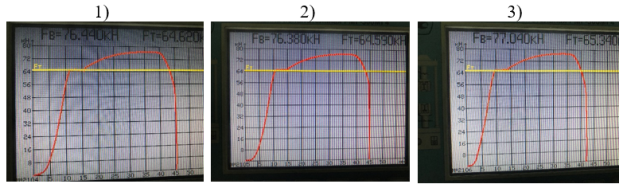
Рис. 3. Данные испытания трёх образцов арматуры на разрыв
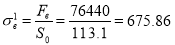
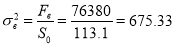
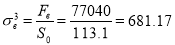
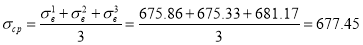
Согласно таблице 7, ГОСТ [9], испытанная арматура относится к классу А500 с модулем упругости
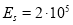
Экспериментальные исследования модели железобетонной балки
Целью эксперимента является моделирование железобетонной балки в уменьшенном масштабе. Исследование были проведены в научно-производственной лаборатории кафедры «Промышленное и гражданское строительство» Таджикского технического университета имени академика М. С. Осими, Министерство образования и науки Республики Таджикистан. Для определения напряжённо-деформированного состояния железобетонной балки были запроектированы и изготовлены три образца модели железобетонной балки (рис.4).

Рис. 4. Физическая модель железобетонной балки
В качестве моделируемого объекта была принята обычная балка прямоугольного сечения 75х150 мм, пролетом 1500 мм. Данная модель железобетонной балки, исходя из расчёта прочности, была армирована в растянутой зоне продольной рабочей арматурой 1 ∅12 А500. В сжатой зоне была армирована конструктивной продольной арматурой 1 ∅6 А240. Соединение двух продольных стержней в обоих зонах осуществлялось поперечными стержнями диаметром 6 А240. Схема армирования модели железобетонной балки приведена на рис. 5. Для измерения перемещения модели балки были использованы механические приборы. Испытание модели балки производилось в положении, соответствующем рабочему положению несущей железобетонной балки.
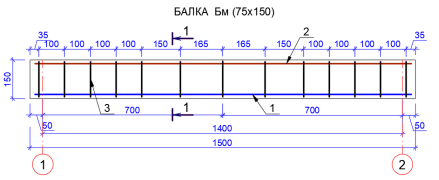
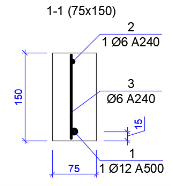
Рис. 5. Армирование модели железобетонной балки
Конструкция испытательного стенда и методика испытания модели балки
Для проведения эксперимента был использован запроектированный и изготовленный испытательный стенд в лаборатории кафедры «Промышленное и гражданское строительство» Таджикского технического университета имени академика М. С. Осими. Испытательный стенд представляет собой плоскую замкнутую раму, которая состоит из вертикальных стоек и верхнего горизонтального ригеля.
Испытание модели железобетонной балки производилось через 30 дней после испытания кубов и призм. Загружение модели производилось двумя сосредоточенными силами, приложенными на одинаковом расстоянии от торцов балки (рис. 6).
Для нагружения образцов модели был использован гидравлический домкрат ДГ50П250 с поэтапным нагружением.
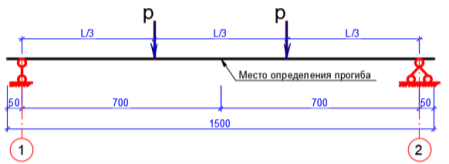
Рис. 6. Схема испытания балки
С целью выделения зоны чистого изгиба, нагрузка на модели балки прикладывалась в виде двух сосредоточенных сил, которые передавались через специально изготовленную металлическую траверсу, выполненную из составного двутавра, усиленной металлическими ребрами. Нагрузка прикладывалась ступенями в зависимости от ожидаемой разрушающей нагрузки.
Значения нагрузки фиксировали с помощью динамометра, установленный непосредственно под домкратом. Перед испытанием образцов динамометр был тарирован. Домкрат снизу опирался на динамометр, а сверху упирался в металлический траверс. В процессе нагружения прогибы измеряли с помощью прогибомера типа ИЧ-50 с ценой деления 0,01 мм, установленный в середине балки. Фотография разрушенных моделей балки приведены на рис. 7.



Рис. 7. Фотографии разрушенных образцов балки
Последовательно увеличивая вертикальную нагрузку на балку, по результатам испытаний получены графики зависимости прогиба в середине пролёта модели от нагрузки (рис. 8).
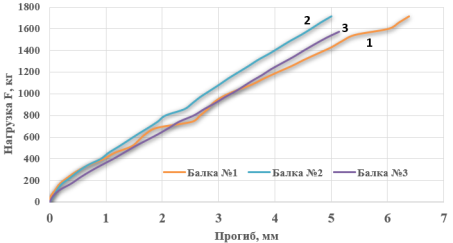
Рис. 8. График зависимости прогиба от нагрузки
При проектировании модель типовой балки были использованы следующие критерии механического подобия [2–8]:
Теория моделирования
Условие одинаковой жёсткости модели и натурной балки. Для это используем уравнение изогнутой оси балки, Дифференциальное уравнение изогнутой оси статически определимой балки можно записать в виде
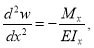
где
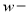
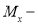
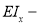
Известно, что уравнение (5) в равной мере описывает закон деформирования, как реальной балки, так и её модели. При этом подобие деформаций и усилий будет обеспечено, если в обеих уравнениях будет соблюдено соотношение сходственных величин. Исходя из теории подобия можно записать
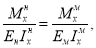
где
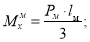
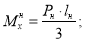
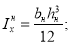
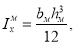
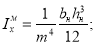
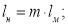
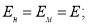
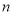
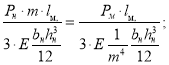
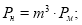
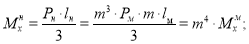
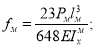
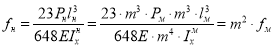
Здесь:
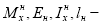
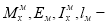
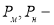
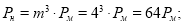
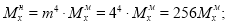
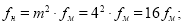
Следует отметить, что в работе [1], при использовании критерия равенства относительных деформаций, констант подобия получается
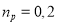
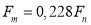
Дальнейшее исследование состоит в проектировании, изготовлении и испытание реальных железобетонных балок, и сравнение полученных результатов модели и балки в натуральной величине.
Результаты и обсуждение.
С целью подтверждения полученных коэффициентов подобия для балки-модели, производили расчёт в программном комплексе ЛИРА-САПР 2017 при одинаковом классе бетона модели и балки в натуральной величине.
Результаты численного моделирования представлены в табл. 2.
Таблица 2
Коэффициенты подобия на основе программного комплекса ЛИРА-САПР
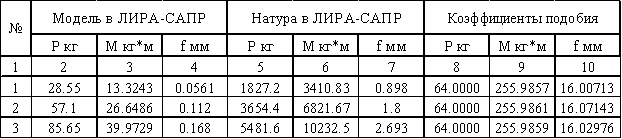
Полученные значения параметров (табл.2): нагрузка, изгибающий момент и прогиб для натурной балки разделим на соответствующие величины модели, получим коэффициенты подобия. Сравнивая полученных коэффициентов с коэффициентами из анализа дифференциального уравнения изогнутой оси балки, можно отметить, что подтверждается правильность предложенной методики определения коэффициентов подобия.
Итоги по смете на расход материала и труда при изготовлении модели и натуральной балки приведены в табл. 3
Таблица 3
Смета расходов материала и труда при изготовлении 3-х натурной и 3-х модельной балки
|
Итоги по смете |
Натурная балка (сомони) |
Модельная балка (сомони) |
|
Материалы |
5327,17 |
131,85 |
|
Машины и механизмы |
129,36 |
2,6 |
|
Итого: |
5456,53 |
134,45 |
Сравнение показывает, что расход материалов и трудоёмкости изготовления модели балки на 97.5 % меньше, чем натурной балки. Кроме того, при натурном испытании возникают значительные трудности, связанные с их изготовлениями и проведением самого эксперимента.
Вывод. Экспериментальным путем исследовано напряженное-деформированное состояние железобетонной балки на моделях. Результаты численного моделирования подтвердили данные, полученные на основе теории моделирования.
Литература:
- Бокарёв С. А., Ефимов С. В. Вопросы подобия усиленных железобетонных балок при экспериментах на уменьшенных масштабных моделях. Интернет-журнал «НАУКОВЕДЕНИЕ» http:// naukovedenie.ru. 2014. Выпуск. 5(24), сентябрь-октябрь, М. — с. 1–12.
- Стельмах С. И. Теоретические основы моделирования балочных конструкций при экспериментах и проектировании. В.сб. ЦНИИСК: «Исследование по расчёту оболочек, стержневых и массивных конструкций». М., 1963.
- Назаров А. Г. О механическом подобии твёрдых тел и его применении к исследованию строительных конструкций и сейсмостойкости сооружений. Известия АН Армянская ССР. Серия тех. наук. Т. XI, № 6, 1958, с. 3–10.
- Назаров А. Г. Основная теорема подобия применительно к моделированию строительных конструкций. Строительная механика и расчет сооружений. № 3, 1959.
- Наносов В. Н. Моделирование строительных конструкций. Стройиздат, М., 1971.
- Мхитарян Д. А. Экспериментальное моделирование бетонных и железобетонных конструкций на статическую нагрузку. Изд. АН Арм. ССР, Ереван, 1987.
- Mkhitaryan D. A. Eksperimental'noe modelirovanie betonnykh i zhelezobetonnykh konstruktsiy na staticheskuyu nagruzku. Izd. AN Arm. SSR, Erevan, 1987.
- 8. Седов Л. И. Методы теории размерностей и теории подобия в механике. Гостехиздат, 1951.
- ГОСТ 34028–2016. Прокат арматурный для железобетонных конструкций. Технические условия. — Введен с 01.01 2018. — 46 с.
- ГОСТ 24452–80. Бетон. Методы испытаний. — Введен впервые 01.01.1982. — М: Стандартинформ, 1980. — 15 с.
- Березин И. С. Методы вычислений. [Текст] / Березин И. С., Жидков Н. П. Том — II. М.:1959 г.
- Бондаренко В. М. Железобетонные и каменные конструкции: [Текст] / Бондаренко В. М., Бакиров Р. О., Назаренко В. Г., Римшин В. Г. Учеб. для строит. спец. вузов // 5-е издание стер. — М.: Высш. шк., 2008. — 887 с.
- Байков В. Н. Железобетонные конструкции [Текст] / Байков В. Н., Сигалов Э. Е. // Общий курс. 5-е издание, переработанное и дополненное. Москва — Стройиздат,1991. 767с.