В данной статье рассматривается особенности создания расчетной модели сталежелезобетонной полностью обетонированной шарнирно опертой балки в ПК Ansys Mechanical c учетом физической нелинейности свойств материалов. В качестве моделирования свойств бетона используется модель Друкера — Прагера. Для стального сердечника и гибкой арматуры применялись описанные в нормативной литературе диаграммы состояния строительных сталей и арматуры соответственно. Получена модель, которую можно использовать в дальнейших исследованиях.
Ключевые слова: Ansys Mechanical, сталежелезобетонная балка, модель Друкера — Прагера, нелинейный расчет, диаграмма состояния стали.
В настоящее время наряду с актуальностью развития методики расчетов и анализа сталежелезобетонных конструкций растет и количество исследований на эту тему [1,2,3,4]. Поэтому остро встает вопрос о нелинейном моделировании пространственных деформируемых твердых тел и их механики в программных комплексах. Для решения таких задач на данный момент активно используется ПК Ansys, в основе которого лежит метод конечных элементов (МКЭ) [5,6].
Цель работы — создать рабочую модель с нелинейными характеристиками материалов в соответствии с СП для использования в дальнейших исследованиях.
Исходными данными для моделирования взята балка сечением 300х500 мм, в качестве жесткой арматуры представлен двутавр 40Б2 по ГОСТ Р 57837–2017 [7], а также четыре стержневые арматуры по верхним углам сечения диаметром 12 мм. Длина балки 6 м.
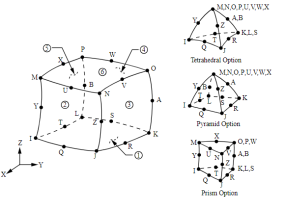
Для моделирования бетона и стального сердечника был использован «SOLID186». Этот элемент определен 20 узлами с тремя степенями свободы на узел: перемещения в узловых направлениях x, y и z. Поддерживает пластичность, ползучесть, жесткость под напряжением, большие прогибы и большие деформации [8]. Для стержневой арматуры использован LINK180. Элемент представляет собой одноосный элемент растяжения-сжатия с тремя степенями свободы в каждом узле: перемещениями в узловых направлениях x, y и z. Поддерживаются пластичность, ползучесть, вращение, большое отклонение и большая деформация [9].
|
|
|
|
а) |
б) |
Рис. 1. a) модель SOLID186 [7], б) модель LINK180 [8]
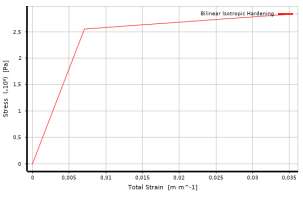
Для стержневой арматуры свойства материалов заданы в соответствии с двухлинейной диаграммой работы арматуры по СП 63.13330.2018 [10]. В Ansys Mechanical принята модель «Bilinear Isotropic Hardening», для которой задается предел текучести и модуль тангенса угла наклона участка прямой пластических деформаций. На рис. 2а представлена диаграмма для стали А500С.
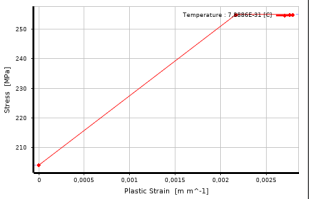
Для жесткой арматуры была принята трехлинейная расчетная диаграмма работы строительных сталей по СП 16.13330.2017 [11], деформации в пластичной стадии ограничены 5 %, так как в дальнейшем исследовании работа сталежелезобетонной балки за пределом текучести не предусматривается. В Ansys Mechanical принята модель «Multilinear Isotropic Hardening», для которой необходимо задать долю пластических деформаций. На рис. 2б представлена диаграмма для стали С255.
|
|
|
|
а) |
б) |
Рис. 2. a) Bilinear Isotropic Hardening для стержневой арматуры; б) Multilinear Isotropic Hardening для жесткой арматуры.
Для задания характеристик и свойств бетона использована модель неупругого деформирования «Drucker-Prager Concrete» [12,13,14]. Для построения начальной поверхности текучести используется три параметра: предел прочности материала при одноосном растяжении, предел прочности при одноосном сжатии и придел прочности при двухосном сжатии [15]. Значения этих параметров представлены на рис. 3 для бетона B40.

Рис. 3. Параметры модели Друкера — Прагера
В ПК Ansys Mechanical существует возможность задать связь между контактными поверхностями. Тип поведения контакта «Bounded» назначается между поверхностью опорных площадок и нижней грани балки. Этот тип поведения контакта не позволяет контактирующим поверхностям проникать друг в друга, а также ограничивает скольжение поверхностей относительно друг друга. Для контакта жесткой арматуры с бетоном задан тип «Frictional», который допускает скольжение поверхностей. Это скольжение определяется коэффициентом трения. В рамках задачи был задан коэффициент 0,1, однако следует регламентировать значение в зависимости от исходных данных и целей проводимых исследований. Тип контакта для связи стержневой арматуры с телом бетона задавался с использованием командной строки APDL, где выделенные параметры — название «Named Selection» для стержневой арматуры и бонтона соответственно:
/PReP7
CMSEL,S, Rebar ,ELEM
NSLE,S
CMSEL,S, С oncrete ,ELEM
CEINTF,0.1
ALLSEL,ALL
/SOLU
Закрепления опорных пластин производилось с помощью «Remote Displacement». Данные представлены в таблице 1.
Таблица 1
Закрепление перемещений и поворотов
|
Тип |
Опора 1 |
Опора 2 |
|
Перемещение X |
+ |
- |
|
Перемещение Y |
+ |
+ |
|
Перемещение Z |
+ |
+ |
|
Поворот X |
+ |
+ |
|
Поворот Y |
- |
- |
|
Поворот Z |
+ |
+ |
Нагрузка задавалась равномерно-распределенной на верхнюю грань элемента. Загружение делилось на 10 шагов.
Тип решатель «Solver Type» использовался прямой «Direct». Прямой решатель считается более надежным и применяется для решения нелинейных моделей с не средовыми элементами, например, балки и оболочки. Остальные параметры вкладки «Analysis settings» заданы по умолчанию «Program controlled». В случае плохой сходимости во вкладке «Step Controls» возможно задать пользовательское значение максимального количества подшагов.
Вывод. Врезультате расчета при загружении балки разрушающей нагрузкой 0,3 МПа получены максимальные напряжения, что свидетельствует о разрушении балки. Результаты представлены в таблице 2. Распределение напряжений в элементах балки представлено на рис. 4–6. Данная модель сталежелезобетонной балки будет использована в дальнейших исследованиях.
Таблица 2
Результаты расчета
|
Элемент |
Напряжение, МПа |
Расчетное сопротивление растяжению (сжатию), МПа |
Отклонение, % |
|
Бетон В40 |
22,617 |
(22) |
2,8 |
|
Жесткая арматура С255 |
255,79 |
255 |
0,3 |
|
Стержневая арматура А500С |
435,98 |
435 |
0,2 |
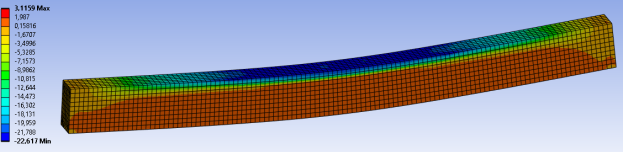
Рис. 4. Распределение напряжений в бетоне
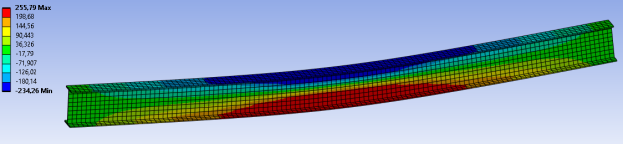
Рис. 5. Распределение напряжений в жесткой арматуре
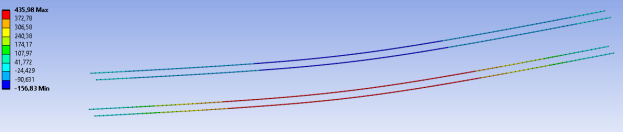
Рис. 6. Распределение напряжений в стержневой арматуре
Литература:
- Замалиев, Ф. С. Расчетно-экспериментальные исследования сталежелезобетонных балок. Известия КГАСУ. 2017. № 4 (42). С. 150–158.
- Mohammad M. El Basha, Tarek K. Hassan, Mohamed N. Mohamed and Omar A. M. Elnawawy, Efficiency of Hollow Reinforced Concrete Encased Steel Tube Composite Beams, International Journal of Civil Engineering and Technology, 9(3), 2018, pp. 720–735.
- Мухамедиев, Т. А. Расчет прочности сталежелезобетонных колонн с использованием деформационной модели. Бетон и железобетон. 2006. № 4. С. 18–21.
- Травуш, В. И. Экспериментальные исследования сталежелезобетонных конструкций, работающих на изгиб. Строительство и реконструкция. 2017. № 4 (72). С. 63–71.
- Krylov, S. B. Contact technologies in design of reinforced concrete beams with cracks. IOP Conference Series. VII International Symposium Actual Problems of Computational Simulation in Civil Engineering, Novosibirsk, Russian Federation: Materials Science and Engineering. 2018. Vol. 456.
- Syahril Taufik, Budi Tjahjono, 3D ANSYS Modeling Behaviour of Encased Steel Composite Column with Wide Flange and Hollow Section, International Journal of Mechanics and Applications , Vol. 9 No. 1, 2019, pp. 10–18. doi: 10.5923/j.mechanics.20190901.02.
- ГОСТ Р 57837–2017 «Двутавры стальные горячекатаные с параллельными гранями полок. Технические условия». Стандартинформ, 2019. 44с.
- SOLID186–3‑D 20‑Node homogeneous. Layered Structural Solid [Электронный ресурс] URL: https://www.mm.bme.hu/~gyebro/files/ans_help_v182/ans_elem/Hlp_E_SOLID186.html. (дата обращения: 15.05.2024).
- 3-D Spar (or Truss). Layered Structural Solid [Электронный ресурс] URL: https://www.mm.bme.hu/~gyebro/files/ans_help_v182/ans_elem/Hlp_E_LINK180.html. (дата обращения: 15.05.2024)
- СП 63.13330.2018 Бетонные и железобетонные конструкции. Актуализированная редакция СНиП 52–01–2003. — М.: АО «НИЦ «Строительство» — НИИЖБ им. А. А. Гвоздева. 2018. — 118 с.
- СП 16.13330.2017 Стальные конструкции. Актуализированная редакция СНиП II-23–81*. — М.: — АО «НИЦ «Строительство» — ЦНИИСК им. В Л. Кучеренко. МГСУ, СПбГАСУ/ 2017. — 139 с.
- Drucker-Prager concrete [Электрон‑ ный ресурс] // Sharcnet. — URL: https://www.sharcnet.ca/Software/ Ansys/17.0/en -us/help/ans_mat/ mat_geomechanics.html (дата об‑ ращения: 19.03.2018)
- Drucker D. C. Relations of experiments to mathematical theories of plasticity // Journal of Applied Mechanics. 1949. № 16. C. 349–357.
- Öztekin E., Pul S., Hüsem M. Experimental determination of DruckerPrager yield criterion parameters for normal and high strength concretes under triaxial compression // Construction and Building Materials. 2016. (112). C. 725– 732.
- Бударин А. М., Плетнев М. В., Алехин В. Н. Численное моделирование изгибаемых железобетонных элементов с использованием критерия прочности Друкера — Прагера. Академический вестник УРАЛНИИПРОЕКТ РААСН. 2018. № 3. С. 74–77.