Сравнение диаграмм деформирования железобетона отечественных и зарубежных норм

В статье автор приводит сравнительный анализ диаграмм деформирования железобетона отечественных и зарубежных норм на примере балочной клетки.

Ключевые слова: диаграмма деформирования, бетон, железобетон, нелинейный расчет, балочное перекрытие.

В современном проектировании нелинейная деформационная модель железобетонного сечения часто используется для расчетов конструкций благодаря своей простоте, универсальности и возможности самостоятельно автоматизировать расчёты с её использованием. Особенностью такой модели является то, что она дает возможность учесть неупругие деформации материалов за счет диаграммы зависимости между напряжениями и деформациями, возникающими в конструкциях. Были рассмотрены три диаграммы: кусочно-линейная и криволинейная по СП63.13330.2018 [1] и криволинейная диаграмма по Eurocode [2].

Линейные диаграммы представляют собой зависимость между напряжением и деформациями с помощью прямых участков, в свою очередь криволинейные — в виде криволинейной линии, состоящей из точек зависимости напряжения и деформаций. Данная зависимость устанавливается: в отечественных нормах через коэффициент упругости, по Eurocode — с помощью коэффициента кривизны K. Данный обзор по диаграммам описан в первой главе работы.

В качестве численно-экспериментальной модели принята каркасная система (см. рисунок 1), которая состоит из колонн и балочного перекрытия. Для исследования зависимости были выбраны различные высоты плиты (от 140 мм до 250 мм) без изменения высоты балки (400 мм). Это было принято, чтобы понять, как влияет отношение плитной части к балочной части на перераспределение усилий в перекрытие. Размер колонн — 400х400 мм, шаг колонн — 6 м. Класс бетона — B25, класс арматуры — А400.

Рис. 1. Расчетная 3D модель

При выполнении физического нелинейного расчета необходимо задать диаграммы деформирования материалов.

На рис. 2 представлены принятые линейно-кусочные диаграммы деформирования для бетона и стали согласно СП 63.13330.2018 [1]. Параметры диаграмм назначаются в зависимости от класса бетона и арматуры и длительности нагружения.

Рис. 2. Линейно-кусочные диаграммы деформирования материалов по СП 63.13330.2018 [1]

На рис. 3 представлены криволинейные диаграммы деформирования бетона и арматуры, которые задавались автоматически в ПК «ЛИРА-САПР», для бетона исходными данными были класс бетона (B25) и тип бетона (ТА).

Рис. 3. Криволинейные диаграммы деформирования материалов по СП 63.13330.2018 [1]

На рис. 4 представлены диаграммы деформирования бетона и арматуры построенные по Eurocode 2 [2].

Рис. 4. Диаграммы деформирования материалов по Eurocode 2 [2]

По итогам расчета были полученные результаты, представленные в табл.1. В качестве сравнение по балке были выделены такие параметры как: значение изгибающего момента в пролете и на опоре балки, перемещение в пролете средней балки.

По результатам расчетов, собранные в табл. 1 и рис. 5–9, можно сделать выводы о том, что при каждом из способов задания диаграмм, получаются примерно одинаковые значения изгибающих моментов My в плите, но при этом можно заметить, что различаются площади зон распределение этих усилий. То есть, при задании криволинейных диаграмм материалов по СП 63.13330.2018 [1] зоны распределения, более очерченные и сконцентрированные, по сравнение с эпюрами по линейно-кусочной диаграмме [1] и диаграммой по Eurocode [2].

Так как основным методом расчета в РФ является расчет по линейно-кусочной диаграмме деформирования материалов, то значения, полученные при этом расчете, принимаем за эталонные. Поэтому можно наблюдать, что значения перемещений в обоих методах отличаются больше, чем на 50 %, то есть, реально возможные деформации при применении данных диаграмм оценивать сложно.

Что касается изгибающего момента в средней балке, то в пролете при расчете по криволинейной диаграмме отечественных норм разница составляет более 20 %, а по Eurocode менее 20 %, но несмотря на это, так же разница присутствует. Значение на опоре имеет другую ситуацию: по криволинейной диаграмме — значения близки к эталонным, по Eurocode — разница составляет ±20 %.

Если в совокупности проанализировать и результаты расчетов по балке, и по плите, то имеем, что более явное перераспределение усилий происходит по нелинейному расчету по линейно-кусочной диаграмме, то есть расчет показывает, что балка включается в работу плиты и забирает на себя часть усилий. Важно отметить, что данное перераспределение усилий и учет приближенного к реальным деформациям перемещения в совокупности влияют на армирование конструкций.

В случае проектирование балочного перекрытия, без учета нелинейной работы материалов, может получиться, что балка в растягивающей зоне будет недоармирована. А более точные значения напряжено-деформированного состояния конструкций позволяют в полной мере проанализировать поведение конструкций.

Таблица 1

Результаты расчета

Примечания: 38,6 % — разница между значением, полученным при нелинейном расчете по л.-к. и значениями, полученными при расчете по криволинейным диаграммам.

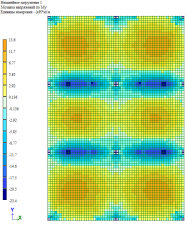
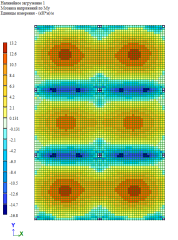
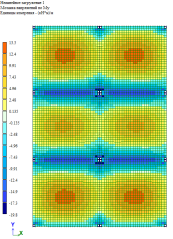
Рис. 5. Изгибающий момент M _y при линейно-кусочной, криволинейной и диаграммам по Eurocode соответственно. Высота плиты 140 мм

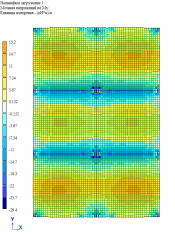
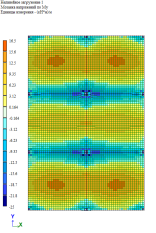
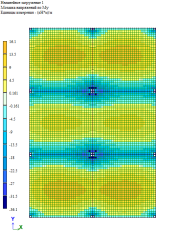
Рис. 6. Изгибающий момент M _y при линейно-кусочной, криволинейной и диаграммам по Eurocode соответственно. Высота плиты 180 мм

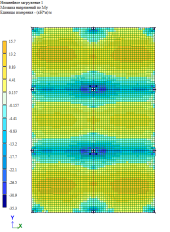
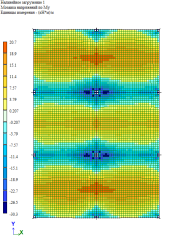
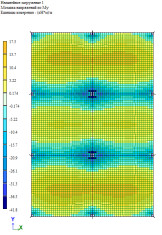
Рис. 7. Изгибающий момент M _y при линейно-кусочной, криволинейной и диаграммам по Eurocode соответственно. Высота плиты 200 мм

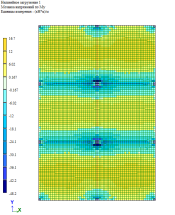
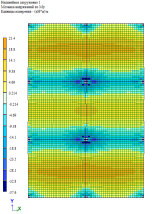
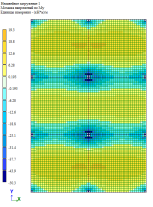
Рис. 8. Изгибающий момент M _y при линейно-кусочной, криволинейной и диаграммам по Eurocode соответственно. Высота плиты 220 мм

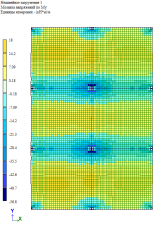
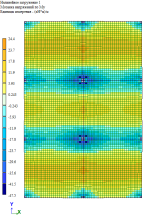
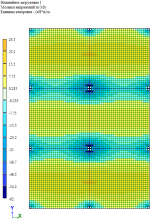
Рис. 9. Изгибающий момент M _y при линейно-кусочной, криволинейной и диаграммам по Eurocode соответственно. Высота плиты 250 мм

Литература:

1. СП 63.13330.2018. Бетонные и железобетонные конструкции. Основные положения. СНиП 52–01–2003 (с Изменением № 1)
2. Eurocode 2: Design of Concrete Structures — Part 1–1: General Rules and rules for buildings. European Committee for Standardization [Text]. — Brussels, 2004. — 225 p.