При математическом моделировании сложных систем широко распространены математические модели случайных процессов, подчиняющихся логарифмически-нормальному распределению. В работе представлен машиноориентированный алгоритм генерации таких процессов, позволяющий генерировать логарифмически-нормальные числовые последовательности с заданными корреляционно-спектральными характеристиками без методических ошибок.
Ключевые слова : методическая ошибка, алгоритм моделирования, логарифмически-нормальное распределение, формирующий фильтр.
In the mathematical modeling of complex systems, the mathematical models of stochastic processes that obey the logarithmic-normal distribution are widespread. The paper presents a machine-oriented algorithm for generating such processes, which allows generating logarithmic-normal numerical sequences with specified correlation-spectral characteristics without methodological errors.
Keywords: logarithmic-normal distribution, methodical error, modeling algorithm, shaping a filter.
Логарифмически-нормальное распределение широко используется в качестве математической модели, описывающей случайные процессы, наблюдаемые в технике, биологии, экономике, при социологических исследованиях и т. п. [1, 2, 3]. Эти процессы используются для описания входных сигналов и признаков сложных систем.
При математическом моделировании как входных сигналов, так и признаков сложных систем требуется генерировать логарифмически-нормальные процессы с заданными корреляционно-спектральными характеристиками [4]. В работе представлен один из возможных подходов решения этой задачи, а именно, генерация логарифмически-нормальных последовательностей с заданной корреляционной функцией с помощью нелинейных формирующих фильтров [3, 5].
Задача моделирования подобных процессов сводится к моделированию числовых последовательностей, являющихся отсчетами моделируемого дискретного случайного процесса …, ξ -3 , ξ -2 , ξ -1 , ξ 0 , ξ 1 , ξ 2 , … ξ n , …, которые имеют логарифмически-нормальную плотность распределения и заданную корреляционную функцию [4].
В общем случае при моделировании подобных процессов моделируется точно либо закон распределения вероятностей отсчетов, либо корреляционная функция отсчетов. В обоих этих случаях при моделировании имеется методическая ошибка, влияние которой на результаты, полученные при моделировании, оценить довольно проблематично.
Эти сложности присущи практически всем алгоритмам моделирования негауссовых процессов, но, при некоторых ограничениях, накладываемых на закон распределения или (и) корреляционно-спектральные характеристики процессов, существуют исключения, позволяющие воспроизводить моделируемый процесс с заданными статистическими характеристиками без методических ошибок [5]. При этом, в отличие от трудно контролируемых методических ошибок приближенных алгоритмов моделирования, вводимые ограничения могут быть учтены точно, а, следовательно, может быть учтено и их влияние на результаты моделирования.
Поскольку требуется моделировать отсчеты дискретного случайного процесса, то будем использовать нелинейные дискретные формирующие фильтры (ДФФ), которые позволяют моделировать практически любые не гауссовские нестационарные процессы. Эффективность машиноориентированных алгоритмов нелинейных ДФФ резко повышается, если ограничиться моделированием приводимых процессов ς( t ).
Под понятием приводимые процессы понимаем нестационарные процессы, для которых существуют функциональные преобразования, позволяющие свести моделирование этих процессов к моделированию известных детерминированных функций и моделированию некоторого стационарного в широком смысле случайного процесса η( t ).
Например, моделирование приводимого нестационарного нормального процесса ς(
t
) с изменяющимися средним значением
m
ς
(
t
) и дисперсией
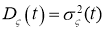
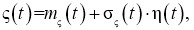
где стационарный в широком смысле процесс с постоянным математическим ожиданием
m
η
=0, среднеквадратическим отклонением σ
η
=1 и корреляционной функцией равной
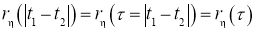
Корреляционная функция
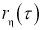
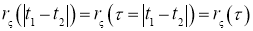
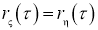
Представление процесса в виде выражения (1) непосредственно используется при моделировании нормальных нестационарных процессов, а при моделировании негауссовых процессов требует некоторой модификации в зависимости от области определения процесса и вида нелинейного преобразования φ(.), обеспечивающего требуемый функциональный вид многомерной (на практике двумерной) плотности распределения вероятностей процесса.
Случайный процесс ξ( t ) может быть получен на выходе нелинейного ДФФ, путем нелинейного преобразования ξ( t )=φ(ς(t)) некоторого «порождающего» процесса ς(t), обычно нормального, как выше (но не обязательно). В этом случае нелинейный ДФФ представляет собой структуру, состоящую из последовательного соединения линейного ДФФ (инерционное звено), на выходе которого формируется процесс ς(t), и нелинейного безынерционного преобразователя φ(ς(t)) (безынерционное звено), после которого и формируется требуемый процесс ξ( t ).
При моделировании процесса η( t ) необходимо обеспечить устойчивость линейного ДФФ, а также, в соответствии с заявленной целью статьи, исключить методические ошибки моделирования. Обе эти цели можно достичь, если ограничиться аппроксимацией корреляционной функции процесса η( t ) в виде экспоненциальных, экспоненциально-косинусных и экспоненциально-синусных кривых, или, что эквивалентно, ограничиться аппроксимацией спектра процесса η( t ) в виде дробно рациональных функций [6]. При этом следует отметить, что выбором соответствующего порядка линейного ДФФ можно добиться требуемой точности аппроксимации реальных (экспериментальных) корреляционных функций [2, 5].
Конкретизируем всё вышесказанное к моделированию логарифмически-нормального процесса. Итак, пусть процесс η(t)
m
η
=0 и σ
η
=1 формируется на выходе линейного ДФФ, сохраняющего закон распределения вероятностей процесса (нормальный) и обеспечивающий заданную корреляционную функцию процесса
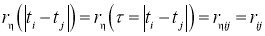
Порождающий процесс ς(t) запишем в виде (1). Тогда, используя функциональное преобразование φ( x )=exp(x), отсчеты дискретного процесса ξ( t i )= ξ i запишутся в виде
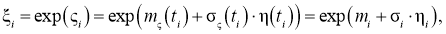
в последнем равенстве индекс ς опущен, η i — случайные нормальные величины с нулевым математическим ожиданием m η =0, единичной дисперсией σ η =1 и корреляционной функцией r ij = r | i - j | = r q , q =0,1,2,…. В работе ограничимся случаем, когда σ i =σ 0 , i =…-2,-1,0,1,2,…, тогда математическое ожидание m ξ i , дисперсия D ξ i и нормированная корреляционной функция r q моделируемого процесс ξ i будут равны
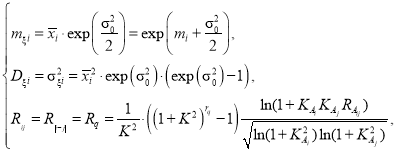
где
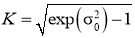
В заключение заметим, что безынерционное функциональное преобразование стационарного процесса приводит к стационарному процессу. Здесь же на вход функционального преобразователя поступает нестационарный процесс, поэтому на выходе стационарного преобразователя также формируется нестационарный процесс, но такой, что при изменении его среднего значения и дисперсии, его нормированная корреляционная функция при ограничении σ i =σ 0 зависит только от разности аргументов, что и позволяет при его моделировании использовать метод формирующих фильтров, предназначенный для моделирования стационарных процессов.
Представленный алгоритм моделирования не содержит методических ошибок при условии, что спектр порождающего нормального процесса аппроксимирован дробно рациональными функциями.
Литература:
- Изранцев В. В., Шепета Д. А. Моделирование внешних сигналов бортовых приборных комплексов летательных аппаратов пятого поколения // Научное приборостроение. — 2000. — Т.10. — № 2. — С. 14–19.
- Подоплёкин Ю. Ф., Шепета Д. А. Имитационные модели и математическое моделирование эхо-сигналов кораблей и морского фона // Морская радиоэлектроника. — 2021. — № 2 (76). — С. 54–57.
- Шепета А. П. Моделирование социально-экономических показателей посредством многоканальных нелинейных дискретных формирующих фильтров // Информационно-управляющие системы. — 2004. — № 4. — С. 49–56.
- Шепета, Д. А. Прямой метод моделирования логарифмически-нормального распределения / Д. А. Шепета, В. И. Исаков, В. А. Тюринова // Волновая электроника и инфокоммуникационные системы: Сб. ст. XXV Междунар. науч. конф. — Санкт-Петербург: Санкт-Петербургский государственный университет аэрокосмического приборостроения, 2022. — С. 135–139.
- Шепета Д. А. Разработка математических моделей и синтез алгоритмов моделирования входных сигналов бортовых систем обработки информации и управления. Диссертация на соискание ученой степени кандидата технических наук / Санкт-Петербург, 2000.
- Марпл. -мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. — М.: Мир, 1990. — 584 с.







