В данной статье рассмотрены методы статистического моделирования применительно к моделированию на ЭВМ случайных процессов, имитирующих непрерывные случайные функции с заданными вероятностными характеристиками.
Ключевые слова: статистическое моделирование, случайные величины, стохастические процессы.
Существуют два типа алгоритмов, при помощи которых на ЭВМ могут вырабатываться дискретные реализации случайного процесса U(t). Алгоритмы первого типа предусматривают вычисление дискретной последовательности значений ![]() , т. е. значений реализаций процесса U(t) в совокупности заранее выбранных моментов времени
, т. е. значений реализаций процесса U(t) в совокупности заранее выбранных моментов времени ![]() . Шаг дискретизации обычно принимается постоянным: ∆t = const, тогда из стационарности процесса U(t) следует стационарность последовательности {
. Шаг дискретизации обычно принимается постоянным: ∆t = const, тогда из стационарности процесса U(t) следует стационарность последовательности {![]() }.
}.
В основе алгоритмов этого типа положено линейное преобразование стационарной последовательности независимых гауссовских чисел ζ с параметрами <ζ> = 0, <![]() > = 1 в последовательность {
> = 1 в последовательность {![]() } коррелированную по заданному закону
} коррелированную по заданному закону
![]() (1)
(1)
где K(τ) корреляционная функция моделируемого процесса. При этом оператор соответствующего линейного преобразования записывается или в виде скользящего суммирования с весом ![]()

или в виде рекуррентного уравнения типа

Вид корреляционной функции воспроизводимого при помощи соотношений (2), (3) случайного процесса определяет набор значений коэффициентов ![]() .
.
Ко второму типу относятся алгоритмы, основанные на представлении моделируемых процессов в виде разложений
![]()
где ![]() некоторая система детерминистических функций; U случайный вектор. При этом моделирование случайного процесса сводится к воспроизведению реализаций векторов U и последующему вычислению значений Um = U(tm) по формуле (4).
некоторая система детерминистических функций; U случайный вектор. При этом моделирование случайного процесса сводится к воспроизведению реализаций векторов U и последующему вычислению значений Um = U(tm) по формуле (4).
Целью статистического моделирования случайных полей является воспроизведение совокупности реализаций значений поля U(x) в дискретных точках ![]() [x = (
[x = (![]() ), n=1,…,N]. В дальнейшем не будем делать формального различия между пространственными координатами и временем и ограничимся случаем однородных случайных полей. Алгоритмы моделирования случайных полей, как правило, являются обобщением соответствующих алгоритмов моделирования случайных процессов на случай m переменных.
), n=1,…,N]. В дальнейшем не будем делать формального различия между пространственными координатами и временем и ограничимся случаем однородных случайных полей. Алгоритмы моделирования случайных полей, как правило, являются обобщением соответствующих алгоритмов моделирования случайных процессов на случай m переменных.
Моделирование гауссовского белого шума.
При статистическом моделировании случайных процессов и полей возникает необходимость в моделировании стационарного дельта-коррелированного гауссовского процесса ζ(t) (белого шума интенсивности s) или его многомерного аналога ζ(x). На ЭВМ можно воспроизводить только усеченный белый шум ζ(f) с конечной дисперсией. Параметр ![]() при моделировании подбирается таким образом, чтобы последовательность ζm = ζ(m∆t) была некоррелированной. Это условие будет выполняться, если выбрать
при моделировании подбирается таким образом, чтобы последовательность ζm = ζ(m∆t) была некоррелированной. Это условие будет выполняться, если выбрать ![]() ∆t где ∆t шаг дискретизации. Моделирующий алгоритм при этом имеет вид [1]:
∆t где ∆t шаг дискретизации. Моделирующий алгоритм при этом имеет вид [1]:

Метод скользящего суммирования для моделирования случайных процессов.
Алгоритм (2) позволяет воспроизводить на ЭВМ последовательности {Um} сколь угодно большой длины, которые с самого начала обладают свойством стационарности. Весовые коэффициенты ![]() могут быть вычислены различными способами. Эффективным является способ, основанный на разложении в ряд Фурье спектральной плотности моделируемого процесса. Преобразование (2) при этом берется в виде
могут быть вычислены различными способами. Эффективным является способ, основанный на разложении в ряд Фурье спектральной плотности моделируемого процесса. Преобразование (2) при этом берется в виде

а коэффициенты

Шаг дискретизации ∆t и число членов ряда P выбираются из условия

где ε — допустимая погрешность; ![]()
Моделирование стационарных случайных процессов с дробно-рациональной спектральной плотностью.
Для моделирования случайных процессов с дробно-рациональной спектральной плотностью вида
![]()
где B(i![]() ) и С(i
) и С(i![]() ) полиномы относительно (i
) полиномы относительно (i![]() ) порядка r и p соответственно (r < p) эффективным является алгоритм типа (3). Спектральная плотность последовательности
) порядка r и p соответственно (r < p) эффективным является алгоритм типа (3). Спектральная плотность последовательности

может быть приведена к виду
![]()
Где
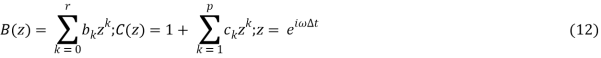
Коэффициенты ![]() используются в рекуррентных уравнениях (3). Соотношения (3) позволяют получать дискретные реализации случайных процессов сколь угодно большой длины. Начальные условия в (3) при вычислении первых значений последовательности {Um} можно выбрать произвольными (например, нулевыми). Вследствие этого возникает переходный процесс, в пределах которого начальный участок вырабатываемой реализации будет искажен. Величина этого участка реализации зависит от корреляционных свойств моделируемого процесса [2].
используются в рекуррентных уравнениях (3). Соотношения (3) позволяют получать дискретные реализации случайных процессов сколь угодно большой длины. Начальные условия в (3) при вычислении первых значений последовательности {Um} можно выбрать произвольными (например, нулевыми). Вследствие этого возникает переходный процесс, в пределах которого начальный участок вырабатываемой реализации будет искажен. Величина этого участка реализации зависит от корреляционных свойств моделируемого процесса [2].
Моделирование случайных процессов с использованием канонического разложения.
Для стационарных гауссовских случайных процессов справедливо разложение:
![]()
где U(ω) и V(ω) — независимые и стохастически ортогональные случайные функции. Принимая, что S(ω) = 0 при |ω| > ![]() и заменяя интеграл конечной суммой, получим:
и заменяя интеграл конечной суммой, получим:

Здесь ![]() гауссовские случайные величины со следующими вероятностными характеристиками:
гауссовские случайные величины со следующими вероятностными характеристиками:
![]()
![]()
Число членов ряда (14) выбирается из условия
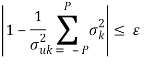
Наряду с (14) можно использовать разложение

Здесь ![]() случайные величины с совместной плотностью вероятности
случайные величины с совместной плотностью вероятности
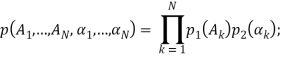
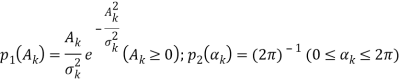 .
.
Реализации, получаемые при помощи выражений (14), (15), являются периодическими (T = 2π/∆ω) следовательно, свойством эргодичности не обладают. Общее достоинство разложений (14) и (15) — простота алгоритма моделирования, а недостаток — необходимость учитывать большое число членов ряда.
Разложения (14) и (15) удобно использовать для получения дискретных реализаций случайных процессов в неравноотстоящих точках [3].
Другие методы моделирования случайных процессов.
Во многих случаях эффективным оказывается метод моделирования, основанный на использовании разложения [4]:

Здесь ![]() случайные величины с совместной плотностью вероятности
случайные величины с совместной плотностью вероятности
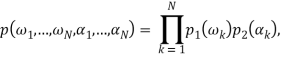
![]()
Согласно центральной предельной теореме распределение реализаций (16) при ![]() стремится к гауссовскому. Кроме того, при
стремится к гауссовскому. Кроме того, при ![]() реализации будут асимптотически эргодическими по отношению к математическому ожиданию и корреляционной функции.
реализации будут асимптотически эргодическими по отношению к математическому ожиданию и корреляционной функции.
Наряду с (16) можно использовать разложение

Здесь ![]() случайные величины с совместной плотностью вероятности
случайные величины с совместной плотностью вероятности
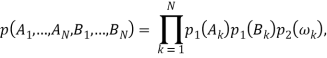
![]()
Кроме того, ![]() Закон распределения величин
Закон распределения величин ![]() можно принять равномерным на интервале (0,1), при этом их реализации моделируются при помощи соотношений
можно принять равномерным на интервале (0,1), при этом их реализации моделируются при помощи соотношений
![]()
Здесь ![]() — случайные числа, равномерно распределенные на интервале (0,1), которые вырабатываются на ЭВМ с помощью программных датчиков. Моделирование реализаций
— случайные числа, равномерно распределенные на интервале (0,1), которые вырабатываются на ЭВМ с помощью программных датчиков. Моделирование реализаций ![]() выполняют одним из методов моделирования случайных величин с заданным законом распределения.
выполняют одним из методов моделирования случайных величин с заданным законом распределения.
Заключение
В данной статье были рассмотрены методы статистического моделирования применительно к моделированию на ЭВМ случайных процессов, заключающихся в решении задачи воспроизведения дискретных последовательностей, имитирующих непрерывные случайные функции с заданными вероятностными характеристиками.
Литература:
- Быков В. В. Цифровое моделирование в статистической радиотехнике. М., «Советское радио», 1971, 328с.
- Голенко Д. И. Моделирование и статистический анализ псевдослучайных чисел на электронных вычислительных машинах. М., «Наука», 1965. 227с.
3. Шведов А. С. Теория вероятностей и математическая статистика. М.: Изд. дом, ГУ-ВШЭ, 2005. — 254с
- Shinozuka M. Simulation of multivariate and multidimensional random processes. — “Journ. Acoust. Soc. Am.”, 1971, vol. 49, N 1, p. 556–583.







