При разработке и исследовании компьютерных систем моделирования в условиях неполной информации мы часто сталкиваемся с наличием различной дискретности контроля «входных — выходных» переменных исследуемого процесса. Подобная ситуация часто возникает при изучении дискретно-непрерывных процессов в технологии, экономике и др. В итоге, исследователь имеет дело с данными, которые могут быть представлены на нижеследующей таблице. Из таблицы следует, что выходная переменная y контролируется реже, чем входная x
Итак, пусть дана выборка, состоящая из s независимых наблюдений случайных величин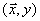 
. При наличии случайных помех, действующих в каналах измерения, где 
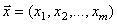, имеются s измерений входной величины 
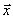. Измерение входной и выходной переменных производятся с разной дискретностью: дискретность измерений 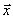обозначим 
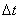, по y — 
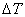, причем имеет место соотношение: 
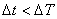. Данные обладают неполнотой по y. Ставится задача восстановления значений выхода и определения целесообразности их использования для задачи моделирования. Таким образом, важно ответить на вопрос: будет ли оценка регрессии с использованием восстановленных y точнее, чем оценка по исходной матрице наблюдений при отбрасывании незаполненных строк в исходной выборке?
Для восстановления значений выхода использовалась непараметрическая оценка функции регрессии [1]:
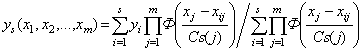, (1)
где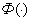 
— ядерная колоколообразная функция и параметр размытости Cs удовлетворяют некоторым условиям сходимости [1, 2].
Методика восстановления недостающих измерений в исходной матрице наблюдений состоит в следующем. Сначала восстанавливается функция регрессии по наблюдениям, полностью представленным в исходной матрице измерений, то есть по полностью заполненным строкам в результате эксперимента. Там, где наблюдения y пропущены, в оценку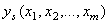 
(1) подставляем значения измеренных 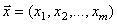и вычисляем соответствующую оценку 
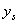, которой восполняем недостающее наблюдение y. Следующий этап восстановления зависимости 
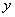от 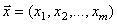состоит в построении непараметрической оценки по всей имеющейся (заполненной) матрице наблюдений. Настройка непараметрической оценки функции регрессии по параметру размытости осуществляется в режиме скользящего экзамена при минимизации среднеквадратической ошибки аппроксимации.
Таким образом, при наличии пропусков необходимо дополнить недостающие строки оценками соответствующих переменных. Как показало достаточно объемное численное исследование изложенного метода, этот прием целесообразно использовать, если доля пропусков более 30 % и менее 80 % от объема исходной выборки.
Результаты вычислений иллюстрируются на рис. 1 и рис.2, где показана квадратичная ошибка приближения функции регрессии по незаполненной (рис. 1) и заполненной (рис. 2) при произвольных значениях вектора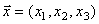 
из куба [0;3].
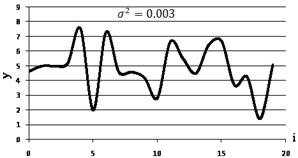
Рис. 2. Восстановление по незаполненной матрице наблюдения
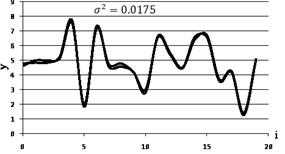
Рис. 3. Восстановление по заполненной матрице наблюдения
Как видно из проведенного эксперимента, восстановление зависимости y = f(x) по заполненной матрице наблюдений оказывается более точным, чем по незаполненной.
Дадим краткую характеристику активным системам, которые можно моделировать на основе предлагаемой методике. К активным процессам относятся такие, которые протекают с участием человека или коллективов людей, а именно: объекты промышленности, коммерческие структуры, региональное образование и многие другие. Характерной особенностью последних являются неполнота априорных данных, неопределенность, взаимосвязанность, трудность формирования согласованных целей и способов их достижения и др. Неполнота априорных сведений приводит к необходимости формулировать те или иные задачи локального характера в различных, принципиально отличающихся постановках, а их объединение в единую систему представляет серьезные теоретические трудности. В частности, задача управления организацией, коллективами во многом остается в большей степени искусством, чем наукой. Обусловлено это тем, что присутствие человека (коллектива) в исследуемом процессе требует учета ряда факторов, а именно: морального, психологического, престижного и других черт и особенностей, свойственных человеку, наиболее важным из которых является искажение информации о своих возможностях, целях, способах и средствах их достижения. Тот или иной организационный процесс можно моделировать, например, по схеме, представленной на нижеследующем рисунке.
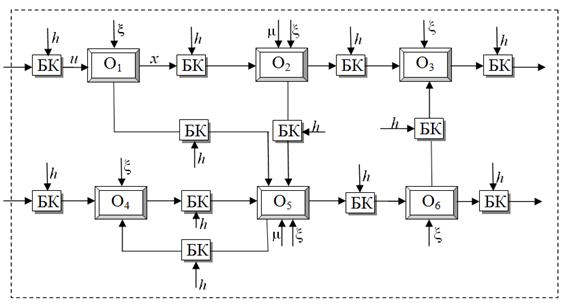
Рис. 4. Схема фрагмента исследуемой системы
На рис. 4 приведена часть системы, элементы которой могут соответствовать различным блокам (технологическим процессам, узлам, отделам обработки и управления). Среди объектов (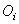
) могут быть как вполне технические, автоматизированные узлы производства, так и блоки, сами по себе являющиеся организационной системой или объектом с участием ЛПР. Блоки контроля (БК) представляют собой измерительные устройства разнообразного характера. Самыми надежными данными могут считаться те, которые получены электрическим способом, но существует и множество других, которые получены в результате химических анализов, технологических испытаний, измерений показателей согласно нормативным актам и прочие. Измерения некоторых переменных в активных системах сопряжено с непосредственным участием человека или экспертов. Вследствие этого возникает необходимость использования различных шкал измерения. Таким образом, задача данной схемы — показать связь разнотипных блоков между собой, где «входные — выходные» характеристики (
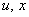) взаимно влияют друг на друга, имеют разную природу, измеряются различными способами и имеют разную дискретность.
Важной составляющей моделирования сложных систем является необходимость работы со случайными помехами, распределенными по конкретному закону. В [4] достаточно подробно изложен метод генерации случайных чисел, распределенных по заданному закону. В настоящее время получены генераторы случайных чисел, распределенных по законам нормальному, Вейбулла, логнормальному, Лапласа и др. На рис. 4 показана гистограмма для закона Лапласа, построенная на основе выборки объемом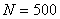 
, количества подынтервалов 
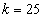, порядка малости 
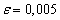[5]. Получившаяся оценка параметра 
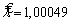при заданном значении параметра 
.
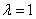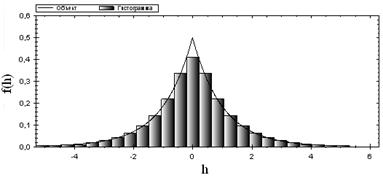
Рис. 5. Гистограмма распределения чисел по закону Лапласа
Рассмотренные выше методы заполнения исходных матриц наблюдений входных выходных переменных и использование датчиков случайных чисел распределенных по различным законам в каналах измерения целесообразно использовать в задачах моделирования организационных процессов.
Литература:
1. Надарая Э. А. Непараметрическое оценивание плотности вероятностей и кривой регрессии. — Тбилиси, Издательство Тбилисского Университета, 1983. — 194 с.
2. Медведев А. В. Непараметрические системы адаптации. — Новосибирск, Наука, 1983.
3. Медведев, А. В. Теория непараметрических систем. Моделирование/ А. В. Медведев // Вестник: СибГАУ. Вып. 4, 2010. — с. 46–53.
4. В. Ф. Первушин, Н. А. Сергеева, А. В. Стрельников. Прецизионный генератор случайных чисел // Вестник: СибГАУ. Вып. 5, 2010. — с. 86–91.
5. Н. А. Сергеева, М. В. Цепкова, Е. А. Чжан. П — генератор случайных чисел по закону Лапласа/ Материалы XV-ой Международной конференции «Решетневские чтения»// Красноярск: изд-во СибГАУ, 2011. — с. 78–79.
