При измерении позиции объекта радаром возникает вопрос о точности измерения. Чтобы минимизировать ошибку измерения используется Фильтр Калмана. Для этого необходимо чтобы измерение было бы выполнено в Декартовых системах координат, но большинство радаров измеряют позицию в полярных или сферических системах координат, и возникает вопрос о линеаризации модели измерения. Ранее для этого была использована формула Тейлора. В этой же статье будет рассмотрен метод минимизации ошибки линеаризации.

Ключевые слова: фильтр, Калман, полярные, сферические, модификация.

1. Обозначения

— n-мерное вещественное векторное пространство

— Множество всех непрерывных функций на множестве [5]

и — Мат. Ожидание и дисперсия случайной величины [8]

— Ковариационна матрица случайного вектора [7]

— След квадратной матрицы [6]

— транспонированная матрицы [6]

— Единичная матрица [6]

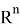
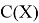
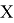
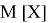
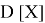
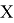
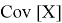
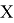
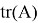
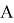
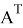
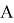
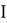
Допустим имеем некоторый движущийся объект в с заданной моделью:

,(1)

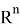
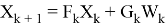
где k-я позиция вектора состояния, - вещественная матрица называемая матрицей перехода, вещественная матрица и есть — мерный Гауссовский случайный вектор т. ч. и .

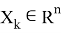
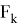
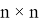
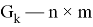
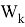
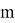
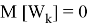
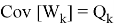
Допустим что некоторое устройство измеряет данный объект с заданной моделью:

,(2)

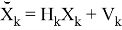
где измерение k-той позиции, есть матрица и есть -мерный Гауссовский случайный вектор т. ч. . и . Рассмотрим оценку вектора состояния на основе измерений

(3)

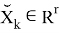
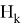
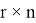
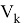
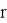
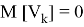
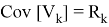
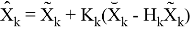
Где и вещественная матрица.

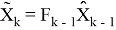
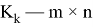
Теорема 1 (см [1] или [2]) Если взять матрицу равной

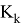
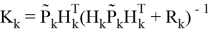
Где определяется рекурсивно

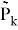
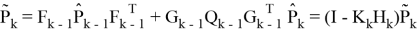
Тогда о есть оценка (3) будет оптимальной.

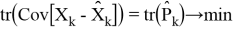
Как можно заметить ковариационная матрица (т. е. ) играет роль в формуле матрицы . Рассмотрим двумерную модель движения [4]: Пусть Т-время между измерениями. Рассмотрим модел состояния в виде

,где . ,где .

. .

. .

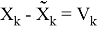
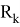
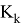
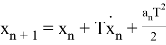
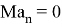
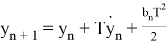
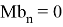
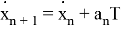
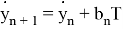
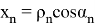
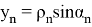
Также модел измерения в виде

, где и . где и .

.

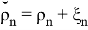
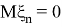
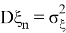
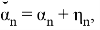
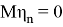
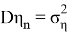
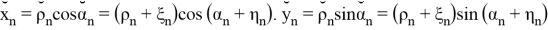
Также Обозначим

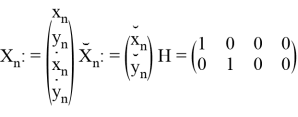
Как можно заметить — модель движения объекта является моделью линейно движущегося объекта со случайным ускорением, но измерение выполняется в полярных систем координат. Проблема заключается в линеаризации и нахождении ковариационной матрицы. Применив формулу Тейлора и отбросив остаточный член получилась следующая оценка ковариационной матрицы [4]

где .(4)

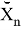
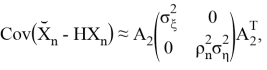
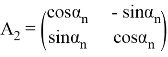
2. Приближение в полярных системах координат

Рассмотрим множество функций

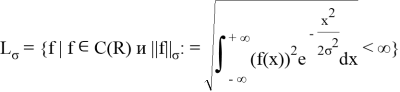
Данное пространство является векторным [6]. Также определим скалярное произведение.

.

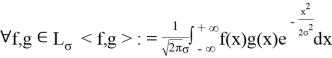
Найдем линейные оценку для в виде

(5)

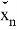
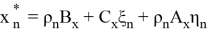
Так чтобы

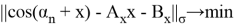
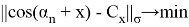
Рассмотрим пространство — множество всех многочленов со степенью не выше чем [3]. есть подпространство , Таким образом наша задача эквивалентна задаче о нахождении и т.ч.

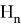
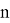
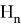
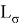
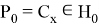
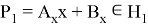
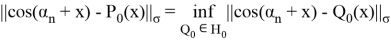
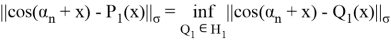
Так как есть базиз в и пространство есть Гильбертово пространство [6, 3], мы можем применить метод неопределенных коэффицентов

(6)

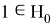
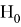
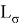
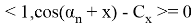
Решив уравнение, имеем

= (7)

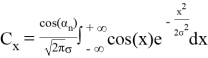
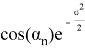
Векторы образуют базис в . Кроме того

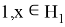
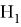
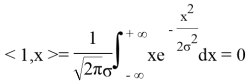
Следовательно система векторов образует базис в [6], следовательно

(8)

(8)

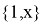
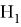
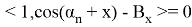
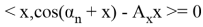
Можем заметить что уравнения (8) и (6) одинаковы, следовательно

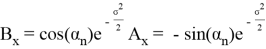
Повторив тот же процесс для y имеем

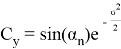
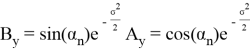
Таким образом мы доказали теорему.

Теорема 2 Оценки и

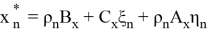
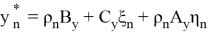
Будут иметь наименьшие значения для и среди линейных оценок.

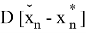
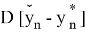
Представив в матричном виде

(2.6)

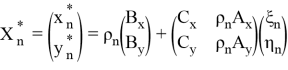
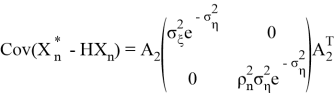
нетрудно заметить, что оценка (1.4) является частным случаем формулы (2.6) когда значение близка к нулю.

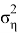
3. Практическое наблюдение при полярных координатах

Ковариационные матрицы (1.4) и (2.6) были использованы при алгоритме фильтрации Kальмана на симуляции при различных значениях .

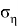
Далее можете видеть результат данной компьютерной симуляции, где

= при использовании ковариационной матрицы (1.4), а — при использовании (2.6)․ Если - то ковариационная матрица эффективенее.

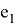
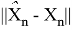
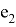
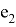
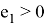
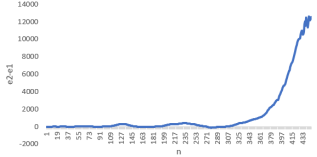
Как видно из полученных результатов, новая ковариационная матрица в большинстве случаев лучше прежней.

Литература:

1. Kalman, R.E. (1960). «A new approach to linear filtering and prediction problems». Journal of Basic Engineering. 82 (1): 35–45. doi:10.1115/1.3662552. Archived from the original (PDF) on 2008–05–29. Retrieved 2008–05–03.
2. Kalman, R.E.; Bucy, R.S. (1961). «New Results in Linear Filtering and Prediction Theory»
3. Hakobyan Y. R. Basics of Numerical Analysis (2005)
4. Ramachandra K. V. (2000) «Kalman Filtering Techniques for Radar Tracking» 1st Edition
5. Дарбинян А. А., Акопян А. Р. (2019) “Модификация фильтра Калмана для полярных и сферических систем координат” Вестник РАУ