Применение алгоритма быстрого преобразования Фурье в системах широкополосного радиомониторинга



В статье автор попытался рассмотреть вопрос применения прямой и обратной формы дискретного преобразования Фурье на основе алгоритма Кули-Тьюки в системах широкополосного мониторинга.

Ключевые слова: радиомониторинг, широкополосный сигнал, прямое дискретное преобразование Фурье, обратное дискретное преобразование Фурье, алгоритм быстрого преобразования Фурье.

Практика показывает, что мониторинг радиоспектра (радиомониторинг) подразумевает одновременное наблюдение за априорно неизвестным количеством источников радиоизлучений [1]. При этом базовой для любой системы радиомониторинга является задача обнаружения несанкционированных сигналов. Эффект и результат радиомониторинга зависит не только от дорогостоящей аппаратуры и правильной установки измерительных приборов, но и от методов, применяемых к этому процессу. Для выполнения поставленных перед комплексами радиомониторинга требований разработчики используют новые технологии, основанные на применении широкополосных (ШПС) и сверхширокополосных сигналов (СШПС). Такие комплексы могут более успешно, чем узкополосные, решать задачи обнаружения и распознавания несанкционированных средств передачи данных в радиосвязи.

В соответствии с [2] к широкополосным относятся системы или сигналы, имеющие относительную полосу частот η в пределах от 0,01 до 0,25, а при η >0,25 они относятся к сверхширокополосным.

В связи с переходом в системах радиосвязи (РС) на широкополосные сигналы (ШПС), при использовании несанкционированных источников передачи данных появилась возможность значительно увеличить скорость передачи информации. В соответствии с известной формулой К. Шеннона [3], при передаче дискретной информации максимальная скорость равна:

C = W• log ₂ [1+P/N ₀ ], (1)

где W — частотная полоса канала связи;

P — мощность сигнала на входе приёмника;

N ₀ — спектральная плотность нормальных аддитивных шумов, равномерная во всей полосе канала.

То есть, основным способом увеличения скорости передачи информации в системе является расширение полосы частот или уменьшение длительности (сжатие) передаваемого сигнала. В реальности теория информации накладывает конечные пределы на возможности сжатия без потерь [4]. Мерой, определяющей эти пределы, является энтропия, характеризующая непредсказуемость информации и рассчитываемая по следующему выражению:

(2)

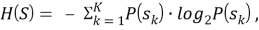
где S — вектор данных, каждый элемент которого может принимать значения s ₁ , s ₂ ,..., s _K с соответствующей вероятностью P(s ₁ ), P(s ₂ ),..., P(s _K ).

Энтропия может принимать значения в пределах:

0 H(S) log ₂ K.

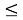
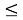
Анализ параметров радиосигналов наряду с их обнаружением составляет одну из основных операций радиомониторинга. В процессе анализа определяются интересующие характеристики обнаруженного радиосигнала, такие как несущая частота, уровень, форма и ширина спектра, параметры модуляции и т. д. В общем случае мощности сигналов и помех на входе обнаружителя — случайные величины, поэтому задача сводится к обнаружению радиосигналов с заранее неизвестными параметрами на фоне помех. В связи с этим исследуемый процесс можно представить как совокупность радиосигналов, наблюдаемых совместно в полосе частот шириной ∆F на фоне аддитивного нормального белого шума (t) неизвестной интенсивности .

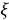
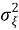
Пусть неизвестное число M радиосигналов S _m (t) , спектры которых, имеющие неизвестную форму, сосредоточены в полосах частот шириной ∆f _m < ∆F (рис. 1).

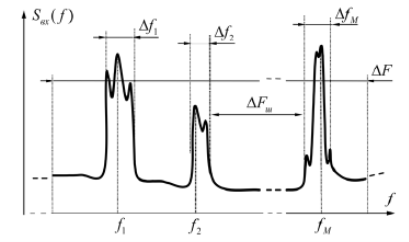
Рис. 1. Спектральная плотность мощности наблюдаемого процесса

Тогда наблюдаемый процесс имеет вид:

(3)

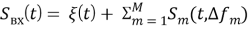
При рассмотрении в качестве исследуемой выборки совокупности отсчетов наблюдаемого во времени процесса S _вх (k) , взятых с интервалом дискретизации T , получаем, что каждый временной отсчет сложным образом зависит от параметров всех присутствующих сигналов. Этот факт затрудняет процесс обнаружения сигналов. Для облегчения решения поставленной задачи необходимо перейти в частотную область, что позволит в качестве вектора наблюдаемых координат использовать отчеты усредненного энергетического спектра анализируемого случайного процесса S _вх (k):

,(4)

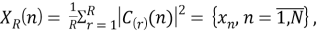
рассчитываемые путем усреднения R спектральных выборок, полученных с помощью прямого дискретного преобразования Фурье (ДПФ, DFT — Discrete Fourier Transform):

.(5)

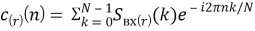
где R — число усредняемых спектров, определяемое числом независимых выборок процесса S _вх (t),

r = – порядковый номер выборки,

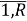
S _вх (t) — анализируемый случайный процесс,

k — номер отсчета во временной области,

n — номер отсчета в спектральной области,

T — интервал дискретизации,

N — размер выборки ДПФ.

Наиболее приемлемым алгоритмом для вычисления дискретного преобразования Фурье является алгоритм быстрого преобразования Фурье (БПФ, от англ. FFT — Fast Fourier Transform), который в Дж.В. Кули и Дж.В. Тьюки описали в своей работе в 1965 г. [5]. Они показали, что можно ускорить вычисления ДПФ с помощью алгоритма БПФ за счет использования свойств симметрии. Данный алгоритм является одним из важнейших алгоритмов обработки сигналов и анализа данных и позволяет получить результат за время, значительно меньшее, чем требуется для прямого, поформульного вычисления (которое вычисляется за O [N ² ] шагов). При применении основного алгоритма дискретное преобразование Фурье может быть выполнено за O(N(p ₁ + p ₂ + … + p _n )) действий, где N = p _1• p _2• … _• p _n . Его применяют при анализе частот в дискретном оцифрованном аналоговом сигнале и т. д.

Согласно алгоритму БПФ Кули-Тьюки число отсчётов (количество компонент разложения) N = N ₁ N ₂

, взятое на некотором ограниченном временном интервале T , выражается как сумма дискретных преобразований Фурье более малых размерностей N ₁ и N ₂ рекурсивно для того, чтобы достичь вычислительной сложности O . Вычислительная сложность О определяет функцию зависимости объёма работы, которая выполняется некоторым алгоритмом, от размера входных данных N . Кули и Тьюки предложили использовать симметрию в каждом из этих вычислений. Поскольку диапазон k равен 0 ≤ k < N , а диапазон n равен 0 ≤ n < M ≡ N/2 (из свойства симметрии) то можно выполнить только половину вычислений для каждой подзадачи. Наше вычисление O [N ² ] стало O [M ² ], где M в два раза меньше N . До тех пор, пока меньшие преобразования Фурье имеют четное M, можно повторно применять разделение, каждый раз вдвое уменьшая вычислительные затраты, пока массивы не станут достаточно маленькими, чтобы стратегия больше не сулила выгоды. В асимптотическом пределе такой рекурсивный подход масштабируется как О [Nlog ₂ N]. Поэтому иногда алгоритм Кули-Тьюки называют алгоритмом прореживания по частоте — времени, имеющим сложность O(Nlog ₂ N).

ДПФ имеет прямую и обратную (ОДПФ, DTFT — discrete-time Fourier transform) форму, т. е. позволяет дискретному сигналу, заданному во временной области, сопоставить его эквивалентное представление в частотной области (дискретный спектр), и, наоборот, по частотной характеристике сигнала позволяет сформировать исходный сигнал во временной области. Обратное дискретное преобразование Фурье (ОДПФ) вычисляют по формуле (6):

(6)

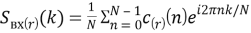
Преобразование из c _r (n) в S _{вх r} (k) является переходом из временной области в частотную, т. е. математически БПФ — это координаты исследуемого сигнала в пространстве, в котором синусоиды выступают в качестве орт. Физически — это частотный спектр сигнала, поэтому данный алгоритм может быть использован для исследования спектра мощности сигнала. Особенностью усредненного спектра (выражение 4) является возможность эффективно накапливать информацию из многих выборок, что позволяет существенно снизить дисперсию получаемых значений по сравнению со случаем, когда R = 1 [6].

Несмотря на то, что БПФ является достаточно быстрым и мощным инструментом исследования спектра сигнала, он не лишён ряда недостатков.

1. Кратность. Основной недостаток БПФ — требование использовать для БПФ только сигналы, у которых длина сигнала в выборках должна быть кратна 2 ⁿ , т. е. при исследовании сигнала с частотой 1 000 Гц гарантированно искажается его спектр, т. к. для БПФ частота сигнала должна быть 1 024 Гц.
2. Дискретность. Сигнал измеряется только в N известных моментах, разделенных в определённые моменты времени временами выборки T, т. е. конечной последовательностью данных. Соответственно информация о его состоянии в промежутках между этими точками отсутствует.

В связи с активным развитием цифровых систем передачи данных в последнее время стали актуальными вопросы разработки алгоритмов цифровой обработки сигналов в системах радиомониторинга, основанные на современных вычислительных методах, одним из которых является вейвлет-анализ. Вейвлет-преобразование устраняет недостатки, присущие преобразованию Фурье, а также даёт частотно-временное представление сигнала.

Литература:

1. Концепция развития системы контроля за излучениями радиоэлектронных средств и (или) высокочастотных устройств гражданского назначения в Российской̆ Федерации на период до 2025 года (Утверждена решением ГКРЧ от 4 июля 2017 г. № 17–42–06).
2. Астанин Л. Ю., Костылев А. А. Основы сверхширокополосных радиолокационных измерений. М.: Радио и связь, 1989. — 192 с.
3. Шеннон К. Работы по теории информации и кибернетики. М.: Иностранная литература, 1963. — 820 с.
4. Волькенштейн М. В. Энтропия и информация. М.: Наука, 2006. — 192 с.
5. James W. Cooley, John W. Tukey. Journal: Mathematics of Computation. 1965, V.19, p.297–301.
6. Рембовский А.М., Токарев А. Б. Автоматизированный радиомониторинг на основе одноканальной и двухканальной обработки данных // Вестник МГТУ. 2004. № 3(56). С. 42–62.