Авторы предлагают применение различных приемов для решения физических задач на аудиторном практическом занятии и самоподготовке.
Ключевые слова: физические закономерности, физические задачи.
Одним из значимых средств формирования мыслительных, творческих способностей курсантов является решение задач, содействующее более глубокому усвоению курса физики, на которой базируются спецдисциплины. Физическая задача как компонента образовательного процесса — это наиболее эффективная форма самостоятельного углубленного изучения и закрепления теории. В процессе решения задействуются все мыслительные операции (наприер, абстракция, анализ, дедукция, обобщение, сравнение, синтез).
Надо отметить, что большинство курсантов на первом курсе испытывают трудности при решении задач. Это связано с формальным запоминанием законов, определений, понятий, формул без уяснения особенностей условий и границ их применимости. В итоге отмечается неверное или безграмотное их применение в конкретных физических условиях. Например, нельзя применять закон Кулона при решении задач на расчет сил, действующих на электрон внутри конденсатора. Или в задачах, связанных с электростатическими явлениями в конденсаторе, не знают, что следует рассматривать только однородные и изотропные диэлектрики, у которых форма их поверхности совпадает с эквипотенциальными поверхностями внешнего поля.
Решить подобные проблемы можно, используя основные принципы обучения педагогики и психологии. Так принципы планомерно-поэтапного формирования умственных действий [1, с. 97] и данные психологических наблюдений над процессом творческого мышления и невозможностью охвата всего объема накопленной информации теоретического и эмпирического характера [2, с. 10] являются хорошим психологическим обеспечением проведения практических занятий по физике и подготовки к ним.
Эта работа должна быть построена на активном взаимодействии курсантов. Совместной деятельности обучающихся в учебных группах с неодинаковым уровнем подготовленности способствуют разнообразные психологические воздействия на личность. Это может быть убеждение, подражание в процессе групповой работы, включающей коммуникативную (обмен информацией), интерактивную (организация взаимодействия) и перцептивную (способность взаимовосприятия) стороны общения.
При таком обучении осуществляются: а) передача полученных знаний друг другу; б) сотрудничество и взаимопомощь; в) реализация обучающимися роли соавтора учебного процесса; г) рефлексия и самоанализ собственных действий. Большой потенциал при работе с учебной группой имеют формы коммуникативного обучения: коллективный фронтальный опрос, взаимоконсультирование курсантов, диалог, групповые дискуссии по конкретным вопросам физики, технология критического мышления (ТКМ), функционирующая по схеме: вызов ↔ осмысление ↔ рефлексия [3, с.146].
Остановимся на ТКМ при использовании на практическом занятии. Этап вызова позволяет уточнить и обобщить наличие знания по данной теме, заинтересовать и мотивировать курсанта к учебе на аудиторном занятии и в часы самостоятельной работы через использование текстов профессионально-ориентированных задач. Этап осмысления ТКМ направлен на получение новой учебной информации и работы с ней. На данной стадии значительный вклад вносят современные средства измерений, информационные технологии, вузовский базовый электронный ресурс тестирования ответов при самостоятельном решении задач. Результатом является конкретный объем знаний. Стадия рефлексии ТКМ нацелена на расширение предметного поля, обращение внимания субъекта на свое сознание, собственную активность.
Для успешного овладения теорией разных разделов физики необходимо предоставить курсанту общие требования по дисциплине: 1) обязательное выполнение индивидуальных заданий, выданных для самостоятельной работы в соответствии с уровнем подготовки; 2) фиксирование задач, решенных на практических занятиях и на самоподготовке, в проверяемую преподавателем отдельную тетрадь; 3) наличие всех конспектов лекций; 4) активность при подготовке к практическим занятиям и на занятиях при решении задач.
Работая по технологии ТКМ на практическом занятии, каждый обучающийся получает индивидуальные задания различного уровня сложности. Вариант заданий определяется преподавателем, который дает общие указания по выполнению заданий и консультирует обучающихся. Курсантам при выполнении задания, выделения этапов решения задач рекомендуем внимательно ознакомиться с соответствующим материалом лекций, прочесть материал учебника, конспекта лекций, методическое пособие теме занятия в соответствии с тематическим планом специальности.
В самом начале занятия обязательно решается задача у доски с пояснениями. В индивидуальных заданиях есть задачи, решаемые по образцу, в которых меняются лишь числовые значения. Они полностью лишены творческого содержания, но необходимы согласно принципам планомерно-поэтапного формирования умственных действий. Неумеющий решать физические задачи курсант должен получить удовлетворение от маленькой победы над собственной неумелостью. Психологический анализ преподавателя умений курсанта должен содержать похвалу.
В ходе обучения решению физических задач в индивидуальных заданиях следует давать стандартные задачи. Любое отклонение от представленного решения показной задачи на доске означает выход за границы рассмотренной ситуации и предполагает поиск нового способа решения. Например, решение задач на расчет емкости плоского воздушного конденсатора (
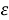
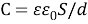
Креативный компонент обучения физике возрастает, если искомое неизвестное формулируется в терминах, не связанных непосредственно с используемой формулой. Например, задача: оружие неподвижного БЛА производит выстрелы во всех направлениях. Найти границу области, простреливаемую из этого оружия, если начальная скорость снарядов известна. Сопротивлением воздуха пренебречь. Для решения данной задачи следует пояснить, что искомая поверхность симметрична относительно выбранной системы отсчета, связанной с позицией БЛА. Или другая задача: вес комплекса радиоэлектронной борьбы «Борисоглебск-2» на горизонтальном участке дороги составляет 21,2 кН. Определить силу тяги для его равномерного движения в гору с уклоном 0,08, если коэффициент трения равен 0,04.
При аудиторном решении физической задачи используются разнообразные приемы, например, прием «тридцати секунд», допускающий произнесение слов одобрения и поддержки на начальном этапе обсуждения с курсантом или всей группой условия задачи и ее физического смысла.
Другим приемом является взаимное обучение. Он состоит в том, что курсант, первый решивший предлагаемую задачу из своего индивидуального задания, обсуждает полученный результат с преподавателем. Затем по просьбе преподавателя при необходимости объясняет суть ее решения другому курсанту, отвечая детально на появившиеся вопросы. Обычно это делается на рабочем месте. Затем они вместе разбирают другой вариант индивидуального задания с аналогичной задачей (например, расчет разветвленных электрических цепей). Изложение вслух понятого материала другому обучающемуся способствует формированию у курсанта уверенности в себе, готовности к взаимопомощи при решении задач, групповой сплоченности.
Следующим приемом является использование бригадной технологии. Учебная группа может быть поделена на малые группы де-юре или де-факто. В случае формального подхода деление на подгруппы проводится на основании локальных актов вуза (по отделениям). При неформальном действии мини группы образовываются самопроизвольно в соответствии с принципом единства предметно-ориентированного и личностно-ориентированного обучения. Внутри мини группы уровень физической и математической подготовленности обычно неодинаков. Но организованные вторым способом мини группы психологически более устойчивы, сплоченны и работоспособны.
Курсанты одной учебной группы первого курса разработали собственный алгоритм подготовки к практическим занятиям по физике: 1) самостоятельное ознакомление с материалом лекции; 2) объяснение смысла физических величин; 3) разъяснение курсанта всей группе у доски законов с приведением простых по смыслу примеров; 4) самостоятельное чтение каждым обучающимся рекомендованной литературы или конспектов по теме предстоящего занятия; 5) заслушивание ответов курсантов и исправление ошибок курсантами с хорошим уровнем подготовки.
Обучение решению задач через представленные технологические приемы позволяют развивать сотрудничество, ответственность за результат, включают курсантов в разнообразные виды созидательной и продуктивной деятельности, способствуют более глубокому усвоению физики, которая является базой изучения общепрофессиональных и специальных дисциплин.
Литература:
- Гальперин П. Я. Четыре лекции по психологии: Учебное пособие для студентов вузов. М.: Университет, Высшая школа. —2010. —297 с.
- Панферов В. Н., Микляева А. В. Принцип целостности в интеграции психологического знания// Психологический журнал. 2019. —Т.40. —№ 2. —С.5–14.
- Сушко Т. И., Хухрянская Е. С., Попов С. В. Технологические приемы критического мышления курсантов при обучении дисциплине «Физика»//Вестник ВИВТ. 2019. —№ 1(28). —С.144–147.

