В статье автор пытается описать систему возможных рисков в 4-х балльной системе, рассчитанных через экспертную систему методом Саати.
Ключевые слова: ремонт, риски, экспертная система, метод парных сравнений, баллы.
В настоящее время существует множество советов по ремонту автомобилей, электрики, сантехники и др. Для того, чтобы обезопасить и оповестить читающего тогда, когда тот решает самостоятельно выполнить работу, не являясь профессионалом в этом деле, был проработан процесс принятия решений, направленный на снижение вероятности неблагоприятного результата и минимизацию возможных потерь, именуемый риск-менеджментом.
Современная экономическая наука представляет риск как вероятное событие, в результате наступления которого могут произойти положительные, нейтральные или отрицательные последствия. Риск относится к спекулятивным рискам, если предполагает наличие как положительных, так и отрицательных результатов. Если же вследствие реализации риска могут наступить либо отрицательные результаты, либо их может не быть вовсе, такой риск именуется чистым [1].
Цель риск-менеджмента — помочь читающему в выборе решения проблем и предупредить его о возможных последствиях и рисках в результате незнания или малого опыта.
Таким образом, возникли следующие задачи:
- Выявить риск и оценить вероятность его реализации и масштаба последствий;
- Разработать риск — стратегию с целью снижения вероятности реализации риска и минимизации возможных негативных последствий;
- Выбрать методы и инструменты управления выявленным риском;
- Непосредственное управление риском;
- Оценить достигнутые результаты и скорректировать риск-стратегию.
Для решения текущих задач пришлось прибегнуть к экспертной системе.
Экспертные системы применяют для моделирования производственных процессов и производственных систем в том случае, когда невозможно формальное описание ситуации, т. е. нет возможности построить математическую модель. Используют неформализованные знания экспертов — специалистов, обладающих солидным опытом и знаниями аналогичных производственных систем.
Известно несколько методов построения экспертных оценок. Предлагается построить экспертную оценку на основе одного из самых распространенных и признанных методов — метода парных сравнений.
Метод парных сравнений основан на попарном сравнении альтернатив [2]. Для каждой пары альтернатив эксперт указывает, какая из альтернатив предпочтительнее (лучше, важнее и т. д.). Ниже рассматриваются алгоритм Саати, реализующий метод парных сравнений [2].
Алгоритм основан на сравнении альтернатив, выполняемом одним экспертом. В качестве эксперта может быть выбран сотрудник, который имеет опыт в сфере ремонта. Для каждой пары альтернатив эксперт указывает, в какой степени одна из них предпочтительнее другой.
Предлагаются пять возможных рисков, с которыми читающий может столкнуться: рисков нет — 0 баллов (обозначим ее как А1), очень маловероятный риск — 1 балл (А2), есть незначительный риск — 2 балла (А3), есть значительный риск — 3 балла (А4), есть точный риск — 4 балла (А5). Решение о возможных рисках, как и говорилось ранее, принимается на основе консультации с экспертом.
Экспертом заполняется матрица парных сравнений размером NxN, где N — количество альтернатив. Матрица заполняется по правилам, приведенным в таблице 1:
Таблица 1
Правила заполнения матрицы парных сравнений для метода Саати
|
Xij |
Значение |
|
1 |
I-я и j-я альтернативы примерно равноценны |
|
3 |
I-я альтернатива менее вероятна j-й |
|
5 |
I-я альтернатива немного предпочтительнее j-й |
|
7 |
I-я альтернатива предпочтительнее j-й |
|
9 |
I-я альтернатива более вероятна j-й |
Если i-я альтернатива менее предпочтительна, чем j-я, то указываются обратные оценки (1/3, 1/5, 1/7, 1/9, 1/11). На главной диагонали ставятся единицы.
Пусть эксперт заполнил матрицу парных сравнений следующим образом (таблица 2):
Таблица 2
Парные сравнения
|
А1 |
А2 |
А3 |
А4 |
А5 | |
|
А1 |
1 |
3 |
5 |
7 |
9 |
|
А2 |
1/3 |
1 |
3 |
5 |
7 |
|
А3 |
1/5 |
1/3 |
1 |
3 |
5 |
|
А4 |
1/7 |
1/5 |
1/3 |
1 |
3 |
|
А5 |
1/9 |
1/7 |
1/5 |
1/3 |
1 |
Здесь, например, X (1,2) = 3 означает, что риск 0 баллов более вероятен, по мнению эксперта, чем 1 балл, поскольку читающий справится с задачей. Элемент X(2,1) = 1/3 означает, что риск 0 баллов менее вероятен, чем 1 балл, т. к. читающий может допустить ошибку, но при этом исправить её самостоятельно.
Затем находятся цены альтернатив (средние геометрические строк матрицы) и их сумма.
Сумма цены (С) альтернатив равна сумме корней N-ой степени из произведения элементов строки.
Для первой строки формула будет выглядеть следующим образом:
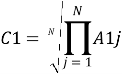
Аналогично и для последующих строк.
Таким образом, сумма будет выглядеть так:
С = 3,94 + 2,04 + 1 + 0,49 + 0,25 = 7,72
После чего необходимо найти веса альтернатив по следующей формуле:
V i = C i /C, где i = 1, …, N.
Таким образом, веса альтернатив следующие:
- V 1 = 3,94/7,72 = 0,51;
- V 2 = 2,04/7,72 = 0,26;
- V 3 = 1/7,72 = 0,13;
- V 4 = 0,49/7,72 = 0,06;
- V 5 = 0,25/7,72 = 0,03.
Наиболее предпочтительной, по мнению эксперта, является альтернатива, имеющая максимальный вес.
Таким образом, по мнению эксперта, наиболее вероятным является риск:
0 баллов — читающий сможет успешно произвести ремонт самостоятельно;
1 балл — может завершить начатый ремонт, и при этом не повредив ничего, и передать то, что он ремонтировал, специалистам самостоятельно.
2 балла — может завершить начатый ремонт, и при этом не повредив ничего, но передать ремонтированную деталь только вызвав специалиста на дом.
3 балла — самостоятельный ремонт невозможен, при этом ремонтированную деталь можно самостоятельно отвезти специалистам
4 балла — самостоятельный ремонт невозможен, ремонтированную деталь отвезти специалистам нельзя.
Благодаря полученной информации была составлена шкала экспертных оценок, где сотрудник может озвучить своё мнение насчёт устранения той или иной причины неисправности читателем самостоятельно.
Это проиллюстрировано на рис. 1.
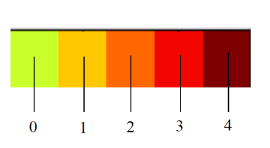
Рис. 1. Тональная шкала рисков.
Литература
- Лельчук А. Л. Актуарный риск-менеджмент. — Москва: Анкил, 2014. — 424 с
- Учебное пособие «Риск-менеджмент. Методы оценки риска». Картвелишвили В. М., Свиридова О. А., ФГБОУ ВО «РЭУ им. Г. В.Плеханова», 121 с.

