В рамках данной статьи были рассмотрены методы машинного обучения для решения задачах нечеткого поиска совпадений в фрагментах текстовых данных в рамках предметной области работы с документами, содержащими перечни материально технических ресурсов. Выделенные методы были оценены с учетом особенностей предметной области и специфики формирования входных потоков данных, были обозначены основные достоинства и недостатки, а также возможность применения методов для реализации алгоритма предобработки данных, в роли которых выступают материально-технические ресурсы.
Ключевые слова: машинное обучение, данные, задачи классификации, нечеткое сравнение.
В настоящее время идет тенденция к тому, чтобы компании, действия которой так или иначе касаются закупкой или поставкой материалов стараются хранить информацию о ресурсах у себя. Это может быть использовано для различных целей: проведение анализа на выборке материалов из множества поставщиков, организация построения логистических путей с учетом множества факторов и т. п.
Для достижения этой цели используются такие технологии как хранилища данных. Однако актуальной проблемой является обеспечение надлежащего качества самих данных, которые приходят от внешних источников. Зачастую проблемой является различия в формате поступающих данных, например, разница между формированием наименования материала у различных поставщиков. Или же возникают проблема с невозможностью точного сопоставления данных из-за возникновения ошибок при занесении информации вручную.
Еще одним фактором является повсеместное применение систем электронного документооборота (СЭД). Однако, большая часть документации участвует в документообороте в виде отсканированных файлов. Для занесения данных в единую информационную систему необходимо использование программ, для распознавания изображений и сканированных документов. Существующие программы распознавания текста значительно упрощают процесс формирования данных, но в тоже время, сами имеют проблемы при распознавании неподготовленных к сканированию файлов, из-за чего зачастую создают ошибки в данных, что затрудняет их дальнейшее использование.
Для этого необходимо применение нечетких методов распознавания и сопоставления новых полученных данных, с уже существующими.
Сейчас большой интерес приобретает использование методов машинного обучения в задачах, которые не имеют однозначного решения, а используется вероятностный подход [1,2].
В рамках данной статьи будут изучены методы, получившие применения в схожих областях и проведен анализ применимости найденных методов к задаче нечеткого поиска совпадений при распознавании текстовых данных.
Классификация является одной из задач информационного поиска, относящаяся к определению объекта классификации к одной из определенных категорий, на основе сформулированных критериев.
Пусть заданы некоторое конечное множество категорий:
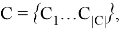
конечное множество фрагментов текстовых данных (далее фрагментов)
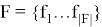
и неизвестная целевая функция Ф, которая для каждой пары <фрагмент, категория> определяет, степень их соответствия:
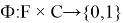
Задача классификации заключается в нахождении максимально близкого классификатора Ф’ к Ф.
Машинное обучение основывается на начальной коллекции фрагментов:
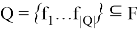
При этом, значение целевой функции Ф известно для каждой пары
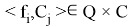
- Учебная. Представляет собой набор фрагментов, для которых находится классификатор.
- Тестовая. Подготовленный набор фрагментов, для которых определено значение целевой функции. Приближение результата вывода классификатора к тестовой коллекции определяет работоспособность и эффективность классификатора.
Фрагмент
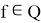
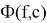
Стоит отметить, что существует два различных наиболее распространённых вида классификации. В зависимости от ответа, классификация бывает:
1. точная:
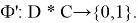
2. ранжированная:
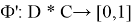
Таким образом, классификация является точной , когда каждой паре <фрагмент, класс> ставится в соответствие булево значение — истина или ложь, то есть, определяет относится ли данных фрагмент к выбранной категории. Второй тип классификации называется ранжированным. Каждой паре <фрагмент, класс> классификатор сопоставляет число, характеризующее степень принадлежности фрагмента к тому или иному классу и лежащее в диапазоне [0,1].
Сейчас математический аппарат методов машинного обучения достаточно развит и существует множество методов решение задач классификации [3,6]. Тем не менее, в зависимости от решаемой задачи и входных условий, методы могут показывать разные показатели эффективности. Машинное обучение является трендом развития технологий, и потому многие предприятия заинтересованы в развитии этой технологии для получения наилучшего качества.
В решении задач классификации наибольшее применение получили следующие типы методов: вероятностные, метрические, логические, линейные, логическая регрессия. Рассмотрим некоторые из популярных методов классификации и определим основные достоинства и недостатки каждого относительно поставленной задачи.
Метод Байеса
(Naive Bayes, NB) относится к категории вероятностных методов классификации. Пусть
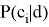
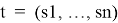
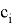
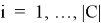
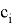
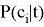
Достоинствами данного метода являются: высокая скорость работы, простота реализации алгоритма, результаты работы алгоритма достаточно просто интерпретировать результат работы, возможность инкрементного обучения, что позволяет непрерывно расширять модель.
Несмотря на приведенные достоинства, метод Байеса имеет так же и минусы в своей реализации. Среди них можно выделить относительно низкое качество классификации и низкая эффективность при соотношении результатов работы алгоритма для одних фрагментов с различными сочетаниями признаков.
При обработке перечня материально технических ресурсов это может быть существенным недостатком, поскольку для дальнейшего внедрения построенного алгоритма может быть необходимо производить классификацию по нескольким критериям сразу.
Метод
k
ближайших соседей
(k Nearest Neighbors, KNN) относится к категории метрических методов. Чтобы найти категорию, соответствующую фрагменту f, классификатор сравнивает f со всеми фрагментами из обучающей выборки L, то есть для каждого
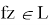
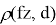
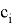
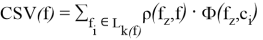
Достоинства данного метода являются: простота реализации, адаптация под нужную задачу выбором метрики или ядра, интерпретируемость результатов.
Однако данный метод имеет ряд существенных недостатков: недостаточная производительность в реальных задачах, так как число соседей, используемых для классификации, будет достаточно большим; трудность в наборе подходящих весов и определением, какие признаки необходимы для классификации; зависимость от выбранной метрики расстояния между примерами, при большом числе объектов сравнения большое время обучения, невозможность решения задач с большим количеством категорий.
Метод опорных векторов (Support Vector Machine, SVM) относится к категории линейных методов классификации. Основной метода является перевод исходных векторов в пространство более высокой размерности и поиск разделяющей гиперплоскости с максимальным зазором в этом пространстве. Две параллельных гиперплоскости строятся по обеим сторонам гиперплоскости, разделяющей классы. Разделяющей гиперплоскостью будет гиперплоскость, максимизирующая расстояние до двух параллельных гиперплоскостей. Идея применения данного метода заключается в том, что чем больше образуется расстояние между параллельными гиперплоскостями, тем более точность определения классификатора.
Достоинствами данного метода являются: задача выпуклого квадратичного программирования хорошо изучена и имеет единственное решение, Принцип оптимальной разделяющей гиперплоскости приводит к максимизации ширины разделяющей полосы, а, следовательно, к более уверенной классификации [7].
Потенциальные недостатки метода опорных векторов заключается в следующем: невозможность калибровки вероятности попадания в определенный класс, подходит только для решения задач с 2 классами, параметры модели сложно интерпретировать.
Для решения задач в рамках предметной области данных алгоритм будет малоэффективных, из-за ограниченности количества классов, на которые могут подразделяться исходные фрагменты.
Метод деревьев решений (Decision Trees, DT) относится к категории логических методов классификации. Деревом решений называют ациклический граф, по которому производится классификация фрагментов, описанных набором признаков. Каждый узел дерева содержит условие ветвления по одному из признаков. У каждого узла столько ветвлений, сколько значений имеет выбранный признак.
Главным преимуществом метода является высокая производительность обучения и прогнозирования, такие деревья решений можно легко визуализировать и интерпретировать.
Основной недостаток метода заключается в том, что для обеспечения высокой точности алгоритма необходим большой объем входных данных.
Данный метод является фаворитом на применение нечеткого поиска среди заданных фрагментов, однако реальную эффективность метода необходимо проверить путем проведения эксперимента и тестовыми данными и определением краевого значения количества тестовых данных, при которых классификатор будет с допустимой полнотой определять классификацию входящих фрагментов.
Нейронные сети являются передовой технологией в решении задач классификации документов и образов. Сейчас большое внимание сконцентрировано на обработке данных, накопленных за время с начала рассвета информационных технологий, и вычислительная мощность современных компьютеров и накопленная теоретическая база позволяет извлечь знания из сохраненной информации.
При решении задач классификации необходимо отнести имеющиеся статические образцы к определенным классам. Наиболее распространенным является способ представления данных, при котором образец представляется в качестве вектора. Компоненты этого вектора представляют собой различные характеристики образца, которые влияют на принятие решения о том, к какому классу можно отнести данный образец. Таким образом, на основании некоторой информации о примере, необходимо определить, к какому классу его можно отнести. Классификатор относит объект к одному из классов в соответствии с определенным разбиением N-мерного пространства, которое называется пространством входов, и размерность этого пространства является количеством компонент вектора.
Большим достоинством применения нейронных сетей в задачах классификации — высокая эффективность и точность классификации. Это обуславливается тем, что в результате обучения нейронной сети создается множество регрессионных моделей (которые используется в решении задач классификации с помощью статических методов).
Однако необходимо понимать, что эффективность обуславливается огромным количеством подготовленных данных для обучения, которые должны покрывать все возможные вариации классификации. Без этого точность и эффективность нейронной сети будет крайне мала, и результат решения задачи не будет достаточно полным.
Рассмотрев особенности указанных методов, можно сказать, что однозначного выбора применяемого метода нет, и необходимо рассмотреть возможности применения методов, исходя из критериев и метрик, которые будут показателями эффективности работы алгоритма над задачей нечеткого сравнения текстовых данных, с учетом особенностей предметной области.
Для более объективного представления об эффективности рассмотренных методов необходимо установить, какого характера данные будут поступать в алгоритм для классификации.
Документы, данные из которых предполагается извлечение информации представляют из себя различные типы документов, в которых имеются ряд уже установленных критериев. которые можно использовать для дальнейшего анализа (наименования материалов, дата поставки, количество, цена, единицы измерения, адрес поставки и пр.). Документы могут быть различных типов и форматов (сканированные документы, табличное представление, выгрузки из базы данных, готовые расчет с перечнем классифицируемых данных). Так как документы изначально поступают в различных форматах и могут иметь различную структуру, это является негативным фактором для классификации, поэтому требуется подготовка данных. Формат подготовленных данных может отличаться, в зависимости от выбранного метода классификации и является одним из факторов оценки конечного алгоритма классификации.
По результатам обзора методов машинного обучения для решения задач нечеткого поиска совпадений в фрагментах текстовых данных, можно сказать, что нет абсолютно точного метода, который гарантированно обеспечить высокую точность определения класса текстового фрагмента ввиду специфических особенностей формообразования используемых фрагментов текста, подвергаемых нечеткому сравнению. Однако уже на основе оценки методов можно предположить какие методы можно исследовать в дальнейшем, а какие далее не рассматривать из-за специфики классифицируемых данных и технологических сложностей не могут быть использованы для дальнейшего применения.
Дальнейшая исследования применения методов машинного обучения к поставленной задаче предполагает реализацию алгоритмов с использованием вышеуказанных методов и проведения экспериментов по классификации подготовленных фрагментов в рамках установленной предметной области.
Литература:
1. Клячкин В. Н. и др. Применение методов машинного обучения при решении задач технической диагностики // Научный вестник УВАУ ГА (И). — 2016. — Т. 8. — С. 158–161.
2. Барахнин В. Б. и др. Автоматизированная классификация русских поэтических текстов по жанрам и стилям // Вестник Новосибирского государственного университета. Серия: Лингвистика и межкультурная коммуникация. — 2017. — Т. 15. — № 3. — С. 13–23.
3. Бабуцкий В. А., Сидоров И. Д. Методы и средства извлечения ключевых слов в задаче автоматической идентификации потенциально опасных текстов в условиях неопределенности их тематической принадлежности // Успехи современной науки. — 2017. — Т. 1. — № 12. — С. 54–59.
4. Комарова А. В. и др. Метод автоматизированного извлечения адресов из неструктурированных текстов //International Journal of Open Information Technologies. — 2017. — Т. 5. — № 11. — С. 21–26.
5. Батура Т. В. Методы автоматической классификации текстов // Программные продукты и системы. — 2017. — Т. 30. — № 1.
6. Краснянский, М. Н., Обухов, А. Д., Воякина, А. А., & Соломатина, Е. М. (2018). Сравнительный анализ методов машинного обучения для решения задачи классификации документов научно-образовательного учреждения. Вестник ВГУ. Серия: Системный анализ и информационные технологии, (3), 173–182. https://doi.org/10.17308/sait.2018.3/1245
7. Метод опорных векторов (SVM). — Текст: электронный // Университет ИТМО. Конспекты: [сайт]. — URL: https://neerc.ifmo.ru/wiki/index.php?title=_Метод_опорных_векторов_(SVM)&oldid=75168 (дата обращения: 21.03.2021).







