Математические методы распознавания образов
Авторы: Худайберганов Тимур Рустамович, Адинаев Хушнудбек Сайлбоевич, Артикбаев Мухаммад Азимжон угли
Рубрика: Спецвыпуск
Опубликовано в Техника. Технологии. Инженерия №2 (4) апрель 2017 г.
Дата публикации: 04.05.2017
Статья просмотрена: 430 раз
Библиографическое описание:
Худайберганов, Т. Р. Математические методы распознавания образов / Т. Р. Худайберганов, Х. С. Адинаев, М. А. Артикбаев. — Текст : непосредственный // Техника. Технологии. Инженерия. — 2017. — № 2.1 (4.1). — С. 45-47. — URL: https://moluch.ru/th/8/archive/57/2318/ (дата обращения: 17.04.2024).
В этой статье написано о математических методах распознавания образов, эффективности и улучшении распознавания образов. Также идёт речь о роли информационных технологий и их достижений. Указаны преимущества Байесовского подхода и алгоритма персептрона.
Ключевые слова: информационные технологии, машинное зрение, ввод и хранение данных, символьное распознавание, диагностика медицины, геология, распознавание речи, распознавание в дактилоскопии, распознавание лица, распознавание подписи и жестов.
Annotation: This article is written on the mathematical methods of pattern recognition, efficiency and improving recognition. Also, there is a speech about the role of information technologies and their achievements. These advantages of the Bayesian approach and perceptron algorithm.
Keywords: information and communication technologies, resources, portal, e-learning, multimedia presentations, animations, static images, dynamic images, global, mapping, modeling, differential training, individual training, distance learning.
Распознавание образов – это научная дисциплина, целью которой является классификация объектов по нескольким категориям или классам. Объекты называются образами. [1,38]
Классификация основывается на прецедентах. Прецедент – это образ, правильная классификация которого известна. Прецедент – ранее классифицированный объект, принимаемый как образец при решении задач классификации. Идея принятия решений на основе прецедентности - основополагающая в естественно - научном мировоззрении.
Задача распознавания образов является основной в большинстве интеллектуальных систем. Рассмотрим примеры интеллектуальных компьютерных систем. [2,124]
1. Машинное зрение. Это системы, назначение которых состоит в получении изображения через камеру и составление его описания в символьном виде (какие объекты присутствуют, в каком взаимном отношении находятся и т.д.).
2. Символьное распознавание – это распознавание букв или цифр.
a. Optical Character Recognition (OCR);
b. Ввод и хранение документов;
c. Pen Computer;
d. Обработка чеков в банках;
e. Обработка почты.
3. Диагностика в медицине.
a. Маммография, рентгенография;
b. Постановка диагноза по истории болезни;
c. Электрокардиограмма.
4. Геология.
5. Распознавание речи.
6. Распознавание в дактилоскопии (отпечатки пальцев), распознавание лица, подписи, жестов.
Формальная постановка задачи классификации.
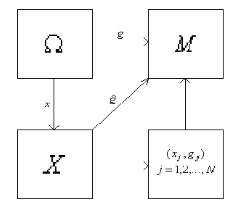
Будем использовать следующую модель задачи классификации. Ω - множество объектов распознавания (пространство образов). : Ω - объект распознавания (образ). g() - Ω M, M={1,2,…,m} - индикаторная функция, разбивающая пространство образов на Ω на m непересекающихся классов Ω1, Ω2 ,…,Ωm. Индикаторная функция неизвестна наблюдателю.
X - пространство наблюдений, воспринимаемых наблюдателем (пространство признаков). x(): Ω X – функция, ставящая в соответствие каждому объекту точку х() в пространстве признаков. Вектор х() - это образ объекта, воспринимаемый наблюдателем. В пространстве признаков определены непересекающиеся множества точек KiX, i = 1,2,…, m, соответствующих образам одного класса. g(x): X M - решающее правило – оценка для g() на основании x(), то есть g(x)= g(x()).
Пусть хj = x(j), j = 1,2,…, N – доступная наблюдателю информация о функциях g() и x()но сами эти функции наблюдателю неизвестны. Тогда (gj,,xj), j = 1,2,…,мN – есть множество прецедентов. задача заключается в построении такого решающего правила g(x), чтобы распознавание проводилось с минимальным числом ошибок. Обычный случай – считать пространство признаков евклидовым, т.е. Х = R1. Качество решающего правила измеряют частотой появления правильных решений. Обычно его оценивают, наделяя множество объектов Ω некоторой вероятностной мерой. Тогда задача записывается в виде minP{ g(x())≠g()}.[4,98]
Классификация на основе байесовской теории решений.
Байесовский подход исходит из статистической природы наблюдений. За основу берется предположение о существовании вероятностной меры на пространстве образов, которая либо известна, либо может быть оценена. Цель состоит в разработке такого классификатора, который будет правильно определять наиболее вероятный класс для пробного образа. Тогда задача состоит в определении “наиболее вероятного” класса.
Задано М классов Ω1, Ω2,…, ΩM , а также P (Ωi|x), i=1,2,…,M вероятность того, что неизвестный образ, представляемый вектором признаков x, принадлежит классу Ωi P (Ωi|x) называется апостериорной вероятностью, поскольку задает распределение индекса класса после эксперимента (a posteriori – т.е. после того, как значение вектора признаков x было получено).
Рассмотрим случай двух классов Ω1 и Ω2. Естественно выбрать решающее правило таким образом: объект относим к тому классу, для которого апостериорная вероятность выше. Такое правило классификации по максимуму апостериорной вероятности называется Байесовским: если P (Ω1|x)> P (Ω2|x), то х классифицируется в Ω1, иначе в Ω2. Таким образом, для Байесовского решающего правила необходимо получить апостериорные вероятности P (Ωi|x), i=1,2. Это можно сделать с помощью формулы Байеса.[3,62]
Итак, Байесовский подход к статистическим задачам основывается на предположении о существовании некоторого распределения вероятностей для каждого параметра. Недостатком этого метода является необходимость постулирования как существования априорного распределения для неизвестного параметра, так и знание его формы.
Линейный классификатор. Алгоритм персептрона. Алгоритм персептрона представляет собой последовательную итерационную процедуру. Каждый шаг состоит в предъявлении нейрону очередного вектора-прецедента и коррекции весов W, по результатам классификации. При этом прецеденты предъявляются циклически, т.е. после предъявления последнего снова предъявляется первый. Процесс обучения заканчивается, когда нейрон правильно классифицирует все прецеденты. Обозначим Wt весовой вектор после t-й итерации, а xt – прецедент, предъявляемый на t-й итерации. Основной шаг алгоритма состоит в предъявлении прецедента очередного прецедента очередного прецедента xi+1.
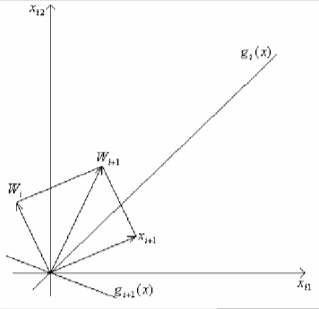
На данном рисунке gt (x) - дискриминантная функция после t - го шага алгоритма; Wt - весовой вектор после t-го шага алгоритма.[4]
Таким образом, задача заключается в построении линейного классификатора в (l+1)M - мерном пространстве так, чтобы каждый из (M - 1)N векторов-прецедентов лежал в положительном полупространстве. Если вектора в исходной задаче разделимы, то это можно сделать с помощью алгоритма персептрона.
Литература:
- Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. Стохастические проблемы обучения. – М.: Наука, 1974.
- Владимиров В.С. Уравнения математической физики. – М.: Наука, 1988.
- Вероятность и математическая статистика: Энциклопедия / Под ред. Ю.В. Прохорова. – М.: Большая российская энциклопедия, 2003.
- Воронцов К.В. Математические методы обучения по прецедентам. Курс лекций (ФУПМ, МФТИ). – www.ccas.ru/voron/teaching.html.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. – М.: Мир, 1985.
Ключевые слова
информационные технологии, распознавание речи, геология, машинное зрение, ввод и хранение данных, символьное распознавание, диагностика медицины, распознавание в дактилоскопии, распознавание лица, распознавание подписи и жестовПохожие статьи
Применение байесовского подхода в измерениях аналитических...
Анализ методов распознавания образов | Статья в журнале... Метод 4. Байесовский подход к принятию решения.
Согласно теореме Байеса [5] вероятность принадлежности высказывания d классу c выражается следующим образом.
Анализ методов распознавания образов | Статья в журнале...
Рис. 2. Евклидово пространство признаков двух классов. Таким образом — первая проблема распознавания
Данная классификация позволяет однозначно определить принадлежность объекта к одному из классов. Метод 4. Байесовский подход к принятию решения.
Устранение полосового шума и зарисовывание пропущенных...
Чтобы ограничить пространство решений в соответствии с априорными знаниями в данной статье мы описываем метод максимума апостериорной вероятности (MAP)
Это может быть вычислено следующим образом. (1.3). Применяя правило Байеса, уравнение (1.3) примет вид.
Контролируемые методы машинного обучения как средство...
Многослойные персептроны (искусственные нейронные сети) были созданы, чтобы попытаться решить эту проблему.
Метод опорных векторов (SVM) предложен Vapnik [8]. SVM преобразует входной вектор в многомерное пространство признаков, а затем получает...
Применение байесовской сети в дифференциальной диагностике...
Байесовской сетью (БС) является графическая модель, отображающая вероятностные
Таким образом, количество ячеек в ТУВ дискретной вершины БС равно произведению
При этом количественная оценка апостериорных вероятностей возможных диагнозов может...
Неконтролируемые методы машинного обучения при...
Таким образом, данные разделены на K кластеров.
При таком подходе основной компонент анализа нейронной сети используется для уменьшения размеров пространства признаков.
Использование апостериорного анализа данных для...
Метод определения весов параметров из набора входящих...
В C4.5 применяется такой вероятностный подход для обработки отсутствующих значений и в обучающих, и в тестовых выборках данных.
Анализ методов распознавания образов | Статья в журнале... Примером этой группы служит байесовский метод принятия решения.
Крайние подходы группировки данных в распознавании образов
Решающее правило в распознавании образов — это алгоритм, который позволяет по результатам измерений определенных признаков объекта
Задача построения решающего правила в условиях полной апостериорной неопределенности достаточно проблематична.
К вопросу о классификации пространств с нечеткими мерами
Пространством с вероятностной мерой или вероятностным пространством называется математическая
Таким образом, может быть получена классификация различных классов пространств с нечеткой
Применение байесовского подхода в измерениях аналитических...
Похожие статьи
Применение байесовского подхода в измерениях аналитических...
Анализ методов распознавания образов | Статья в журнале... Метод 4. Байесовский подход к принятию решения.
Согласно теореме Байеса [5] вероятность принадлежности высказывания d классу c выражается следующим образом.
Анализ методов распознавания образов | Статья в журнале...
Рис. 2. Евклидово пространство признаков двух классов. Таким образом — первая проблема распознавания
Данная классификация позволяет однозначно определить принадлежность объекта к одному из классов. Метод 4. Байесовский подход к принятию решения.
Устранение полосового шума и зарисовывание пропущенных...
Чтобы ограничить пространство решений в соответствии с априорными знаниями в данной статье мы описываем метод максимума апостериорной вероятности (MAP)
Это может быть вычислено следующим образом. (1.3). Применяя правило Байеса, уравнение (1.3) примет вид.
Контролируемые методы машинного обучения как средство...
Многослойные персептроны (искусственные нейронные сети) были созданы, чтобы попытаться решить эту проблему.
Метод опорных векторов (SVM) предложен Vapnik [8]. SVM преобразует входной вектор в многомерное пространство признаков, а затем получает...
Применение байесовской сети в дифференциальной диагностике...
Байесовской сетью (БС) является графическая модель, отображающая вероятностные
Таким образом, количество ячеек в ТУВ дискретной вершины БС равно произведению
При этом количественная оценка апостериорных вероятностей возможных диагнозов может...
Неконтролируемые методы машинного обучения при...
Таким образом, данные разделены на K кластеров.
При таком подходе основной компонент анализа нейронной сети используется для уменьшения размеров пространства признаков.
Использование апостериорного анализа данных для...
Метод определения весов параметров из набора входящих...
В C4.5 применяется такой вероятностный подход для обработки отсутствующих значений и в обучающих, и в тестовых выборках данных.
Анализ методов распознавания образов | Статья в журнале... Примером этой группы служит байесовский метод принятия решения.
Крайние подходы группировки данных в распознавании образов
Решающее правило в распознавании образов — это алгоритм, который позволяет по результатам измерений определенных признаков объекта
Задача построения решающего правила в условиях полной апостериорной неопределенности достаточно проблематична.
К вопросу о классификации пространств с нечеткими мерами
Пространством с вероятностной мерой или вероятностным пространством называется математическая
Таким образом, может быть получена классификация различных классов пространств с нечеткой
Применение байесовского подхода в измерениях аналитических...







