The talented mathematician Frank Plumpton Ramsay proved that total disorder is impossible. Every sufficiently large set of numbers, points, or objects necessarily contains a highly ordered structure.
Specialists in Ramsey's theory try to calculate how large a set of stars, numbers or objects must be in order to guarantee the existence of a certain desired substructure. Such problems often take decades to solve, and they only lend themselves to the most inventive and subtle reasoning. By trying to find solutions to the problem at hand, experts in Ramsey's theory are thus helping engineers to build better communication networks and systems for transmitting and retrieving information. They have also discovered some mathematical methods that will be of use to scientists of the next century. Perhaps most importantly, Ramsey's theory explores the underlying structure of mathematics, that is, the structure that pervades the entire universe.
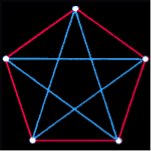
Unlike many sections of modern mathematics, Ramsey's theory can be stated on an intuitive level. Indeed, the attractiveness of this theory is due in part to the simplicity with which its problems can be formulated. For example, if six people (say, Alfred, Betty, Calvin, Deborah, Edward, and Frances) are randomly selected from those present at a party, is it true that either three of them know each other, or three of them are strangers to each other?
We could solve this «party puzzle» in many ways. We could go through every conceivable combination and test whether each group in question contains three people we know or three people we don't know. But since we would have to check 32768 (or 215) combinations, this «brute force method» is neither practical nor instructive.
Fortunately, we can find the answer by looking at two simple cases. In the first, suppose Alfred knows three (or more) of the other guests, say Betty, Calvin, and Deborah. If Betty and Calvin, or Betty and Deborah, or Calvin and Deborah know each other, then Alfred and the pair of acquaintances form a group of three familiar people; otherwise, Betty, Calvin, and Deborah are strangers to each other. In the second case, suppose Alfred knows at most two (or fewer) of the guests, say Betty and Calvin. If Deborah and Edward, or Deborah and Francis, or Edward and Francis are strangers to each other, then Alfred and a pair of strangers to each other form a group of three strangers to each other. Otherwise, Deborah, Edward, and Francis know each other. In just six sentences, we have proved why any group of six must include either three people who know each other or three people who don't know each other. In short, the solution to the «party puzzle» is a special case of Ramsey's theory.

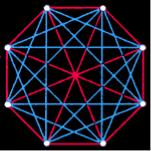
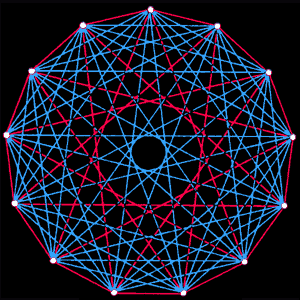
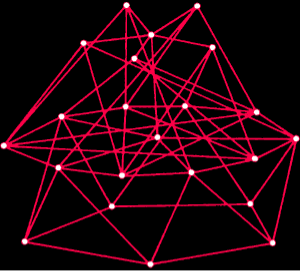
Fig. 1. The party puzzle is a problem typical of applications of Ramsey's theory. How many people are there enough to form a group in which there will always be either four people who know each other, or four people who do not know each other? In this figure, the guests are represented by dots. Each red edge in the graph connects guests who know each other, and each blue edge connects those who do not know each other. In the group of 17 dots depicted in the figure it is impossible to find four dots for which the network of connecting edges would be entirely red or entirely blue. Therefore more than 17 people are needed so that among them there are necessarily either four people who know each other or four people who do not know each other. In fact, in any group of 18 people there will always be either four people who know each other, or four people who don't know each other.
Generalizing this particular case, we can formulate the theorem in its full form. Instead of six people, as in this problem, we can take any number of people or, if you like, any number of objects. In addition, there is no need to be limited to two types of relationship, acquaintance and stranger. We can take any number of mutually exclusive relationships--for example, friends, enemies, and observing neutrality.
Ramsey's theory can be formulated even more generally. If the number of objects in the set is large enough, and every two objects are connected by one of a set of relations, then there is always a subset of the set that contains a given number of objects, and such that all objects in it are connected by a relation of the same type.
Frank Ramsay, who first proved this statement in 1928, grew up in Cambridge, England. His father, Arthur S. Ramsay, was professor of mathematics and president of Magdalene College, Cambridge University. In 1925 the young Ramsay, recognized as the best student in mathematics, graduated from the university. Although he was most interested in philosophy and mathematical logic, he also wrote papers on economics, probability theory, decision-making, cognitive psychology and semantics.
There is a certain irony in the way in which, two years before his death, Ramsay derived the theory that now bears his name. He arrived at the basic idea by trying to prove the thesis advanced by Russell and Alfred North Whitehead in their seminal work Principia Mathematica. They suggested that all mathematical truths could be derived from a limited set of axioms. Developing this idea, the German mathematician David Hilbert suggested that there must be a procedure for deciding whether or not a given statement follows from a given set of axioms. Ramsay showed that in some particular case such a decision procedure existed. (A few years later Kurt Gödel and his followers, the Englishman Alan Turing and others, proved exhaustively that no such procedure exists in the general case.)
Ramsay proved his theorem as a first step, trying to demonstrate the validity of Russell's thesis in the special case. As it turned out, he could have accomplished this task by other means. Earlier, Ramsay had proved a theorem irrelevant to the thesis he had justified, which he would never have been able to prove in the general case.
This was the case until 1933, when two Hungarian mathematicians, Paul Erdős and George Szekeres, rediscovered Ramsey's theory. It was largely due to their efforts that the theory became popular among mathematicians. At the time, Erdős was a nineteen-year-old student at the University of Budapest, while Szekeres had shortly before that obtained a degree in chemical engineering from the Budapest Polytechnic Institute. Together with a group of student friends, they met almost every Sunday in a country park, mostly to talk about mathematics.
In the winter of 1933, one of the students, Esther Klein, asked them to solve a curious problem; to prove that if five points in a plane were placed in such a way that no three points lay on the same straight line, then they would certainly find four of them which formed a convex quadrilateral. (Convex figures include, say, a regular hexagon, but not a five-pointed star. More strictly, a polygon is called convex if every segment connecting its vertices lies inside that polygon.)
What about Ramsey's number for five red and three blue? In other words, what is the smallest complete network, which, if randomly colored in red and blue, would necessarily contain either a red network of five points or a blue network of three points? Ramsey's number for five red and three blue is 14, which was proved only in 1955 by Robert Greenwood of the University of Texas at Austin and Andrew Gleason of Harvard University.
|
|
|
|
|
5 < R(3,3) = 6 |
8 < R(3,4) = 9 |
13 < R(3,5) = 14 |
|
|
| |
|
17 < R(3,6) = 18 |
22 < R(3,7) = 23 | |
|
|
| |
|
27 < R(3,8) ≤ 29 |
35 < R(3,9) = 36 | |
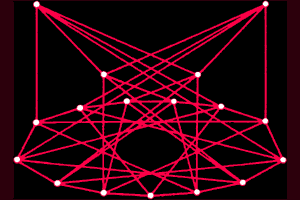
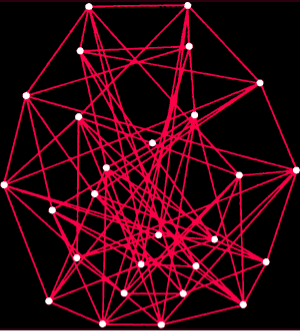
Figure 2. Ramsey numbers are defined as the smallest value of n for which in any group of n points either some group of j points forms a complete network of red edges, or some group of k points forms a complete network of blue edges. The figures show how large a particular Ramsey number must be. The first diagram shows five points connected by red and blue edges in such a way that no three points form either red or blue complete network. Consequently, it can be deduced from the first diagram that the Ramsey number for three red and three blue edges is greater than five. Similarly, it can be argued that the second diagram implies that the Ramsey number for three red and four blue is greater than eight. By other more complicated methods it can be shown that Ramsey's number for three reds and three blues is six, and Ramsey's number for three reds and four blues is nine. All known Ramsey numbers are given above, except the Ramsey number for four reds and four blues, for which the diagram is shown in Fig. 1. (In some diagrams the blue edges are not shown for simplicity.) With respect to the Ramsey number for the three reds and eight blues, it has been proven that it is greater than 27 and less than or equal to 29. Recently it has been shown (but not yet confirmed) to be 28.
Ramsey numbers are extremely difficult to compute. Through the efforts of generations of mathematicians and computers, we were able to find only seven Ramsey numbers, which are shown in Fig. 2. To illustrate the difficulty of calculating Ramsey numbers, Erdösh often tells the following anecdote. Aliens have invaded the Earth and threaten to destroy it in a year if humanity cannot find the Ramsey number for the five reds and five blues. We could mobilize the best minds and the fastest computers, and then within a year we might be able to find the value. But if the aliens demanded that we find Ramsey's number for the six reds and six blues, we would have no choice but to strike preemptively.
Erdösh did find a way to get some idea of how big the Ramsey number must be. What if he could find a red and blue coloring of a large full net containing neither a red nor a blue net of three dots? Such a coloring of a complete net of five points is shown in Fig. 2. It follows that the Ramsay number for three red and three blue must be greater than five. Five is the lower limit for this Ramsey number.
In 1947, Erdős proposed an unusual method of finding the lower bound of any Ramsey number: the flip of a coin. He attempted a mental experiment in which each edge of a complete network of, say, a million points was colored according to the tossing of a «real» coin (i.e., a coin for which the probability of heads or tails is exactly the same and equal to 1/2. — Translation). The edge is colored red if tails rolls and blue if heads rolls. He then tried to prove that Ramsey's number for, say, 34 reds and 34 blues is greater than a million. The experiment is considered successful if no red or blue network of 34 dots results from such random coloring.
How would he guarantee success? Any 34 points are connected by 561 edges. If the first throw prescribes a blue color for the first edge, then to get a blue network, the next 560 throws must also prescribe a blue color. The probability that this will happen is 2–561. The probability of a red net occurring is exactly the same, so the total probability of a one-color net occurring is double, or about 2.6×10–169.
Now recall that the number of sets of 34 points chosen from a million points is
|
1000000! 34! · 999966! |
≈3,4×10 165 . |
Thus we can expect that of all possible complete networks of 34 points, 3.4×10165×2.6×10–169, or approximately 0.001, will be monochrome. So, in 99.9 % of cases the mental experiment will be successful, single-color sets of 34 points will not occur.
Erdősz then applied a subtle contrary proof. He assumed that no coloring scheme was successful. Then the mental experiment would have a zero probability of success, which he already knows is not true. So this assumption must be wrong, i.e., there must be a successful coloring scheme (not with 99.9 % probability, but with absolute certainty). The existence of such a coloring scheme means that one million is the lower bound for 34 reds and 34 blues.
This reasoning, known as the probabilistic method, gives the best lower bound estimates for the Ramsey numbers. However, this method gives no indication of how the desired coloring should actually be produced. In attempts to obtain such colorings, researchers use a rich arsenal of techniques from number theory, set theory, and other branches of mathematics. Although the results obtained are interesting, they do not yet reach the estimates given by the coin flip method.
Much of the early research on Ramsey's theory focused on sets of points and lines, but still many of these studies also dealt with sets of numbers. The Dutch mathematician Barthel L. van der Varden began to solve such problems even before Ramsey proved his theorem.
In 1926, van der Varden encountered an interesting problem related to arithmetic progressions. As the name itself suggests, an arithmetic progression is a sequence of numbers in which the difference between two adjacent terms remains constant. For example, the sequence 3, 5, 7 is a three-member arithmetic progression in which the difference between the adjacent terms is two. A particular case of the problem that attracted Van der Varden's attention can be formulated as follows. If every integer from 1 to 9 is printed on a page in one of two colors, red or blue, will there always be three blue or three red numbers which form an arithmetic progression? The answer is given in the following box.
Ramsey's theory and arithmetic progressions
An arithmetic progression is a sequence of numbers in which the difference between adjacent terms remains constant. For example, 7, 10, 13, 16 is an arithmetic progression in which the difference between the adjacent terms is three. The following statement about arithmetic progressions follows from Ramsey's theory: if each number from 1 to 9 is colored red or blue, then either three blue numbers or three red numbers will form an arithmetic progression.
To prove this statement, we could check all 512 ways of coloring the nine numbers. But we can prove it by considering only two cases. Let's start with the case in which 4 and 6 have the same color, say blue.
1 2 3 4 5 6 7 8 9
To avoid the blue arithmetic progression 4, 5, 6, we will paint 5 red.
1 2 3 4 5 6 7 8 9
To avoid the blue arithmetic progressions 2, 4, 6 and 4, 6, 8, we will paint 2 and 8 red.
1 2 3 4 5 6 7 8 9
But then we have a red arithmetic progression of 2, 5, 8. So, if 4 and 6 have the same color, we always get either a red or a blue arithmetic progression. Now consider the case where 4 and 6 are different colors. The number 5 can be colored any way we want without creating an arithmetic progression, so we will arbitrarily paint 5 red.
1 2 3 4 5 6 7 8 9
Let's continue coloring as follows:
3 to avoid 3 4 5
9 to avoid 3 6 9
7 to avoid 5 7 9
8 to avoid 6 7 8
2 to avoid 2 5 8
1 to avoid 1 2 3
This coloring gives a sequence of
1 2 3 4 5 6 7 8 9
But there is still a red arithmetic progression of 1, 5, 9. Thus, regardless of whether 4 and 6 are colored the same or differently, there is always either a blue or a red arithmetic progression.
Van der Varden set himself the following problem, which is a generalization of the previous one: to prove that if n is a sufficiently large number, and all integers from 1 to n are printed on the page in one of two randomly chosen colors for each digit, then there always exists a one-color sequence with a certain number of members, which is an arithmetic progression. This statement can be considered Ramsey's theorem for arithmetic sequences, although it is commonly known as Van der Varden's theorem.
Van der Varden enlisted the help of his colleagues Emil Artin and Otto Schreyer. He later wrote: «We went to Artin's study in the Mathematics Department of the University of Hamburg and tried to find a proof. We drew some drawings on the blackboard. We had what the Germans call an Einfälle (epiphany) state, when unexpected ideas come to mind. Several times such new ideas steered the discussion in a new direction, and one of them finally led to a solution. It turned out, however, that Van der Varden could not prove this result for two colors without proving it for the case where an arbitrary number of colors are used simultaneously.
In his proof, van der Varden applied a special kind of mathematical induction. The usual (single) induction involves two steps. The first step is to show that the statement holds for some small number, say two. The second step proves that if the statement is true for some number, then it is also true for a number one larger. It follows that it is true for three, four, and so on. The results «come in hand after hand» like an endless line of falling dominoes placed on an edge: if you push one, all of them will fall.
To prove Ramsey's theorem for arithmetic progressions, van der Varden applied a more subtle, double induction. He assumed that for any fixed number of colors, there exists a number n such that if every integer in the interval from one to n is printed with some of these colors, an arithmetic progression of numbers of the same color, consisting of, say, 10 members, will be found. Based on this assumption, he was able to show that for any fixed set of colors there exists a number m such that if every integer in the interval from 1 to m printed with any of these colors, there will be a one-color arithmetic progression of 11 members. In general, he showed that from the results for k members and any number of colors the result for k+1 members and any number of colors follows.
After van der Varden got to this stage of the proof, he only had to demonstrate that his assumption is indeed true for some small value of k. If there are more integers than colors, there are always two numbers of the same color. These two numbers form an arithmetic progression of two terms. So a one-color arithmetic progression always exists if there are one more numbers than colors. An infinite sequence of dominoes for two members now collides an infinite sequence of dominoes for three members, which in turn collides an infinite sequence of dominoes for four members, and so on (see the next box).
References:
- A. M. Gleason and R. E. Greenwood. Combinatorial Relations and Cromatic Graphs. In: Canadian Journal of Mathematics, 1955, v.7, No.1, pp.1–7.
- B.L. van der Waerden. How the Proof of Baudet's Conjecture Was Found. In: Studies in Pure Mathematics (Edited by L.Mirsky). Academic Press, Inc., 1971.
- Paul Erdös: The Art of Counting: Selected Writings (Edited by Joel Spencer). The MIT Press, 1973.
- Paul Hoffman. The Man Who Loves Only Numbers. In: Atlantic Monthly, 1987, v.260, No.5, pp.60–74.
- R. L. Graham and V.Rödl. Numbers in Ramsey Theory, in Surveys and in Combinatorics. London Mathematical Society Lecture Notes Series, 1987, No.123, pp.111–153.
- Ronald L.Graham, Bruce L.Rothschild and Joel H.Spencer. Ramsey Theory. Second Edition. John Wiley & Sons, Inc., 1990.