Математическое моделирование типовых очагов горения в начальной стадии при помощи программы FDS (Fire Dynamics Simulator)

Математическое моделирование процессов горения все более часто используется в научных разработках, а также при расследовании пожаров. Развитие теории математического моделирования горения, а также увеличение вычислительной мощности компьютеров позволило существенно сократить требуемые ресурсы, а также повысить точность моделирования. Одной из областей применения результатов математического моделирования динамики пожара является тестирование интеллектуальных алгоритмов работы автоматической пожарной сигнализации. Проведение огневых испытаний всегда трудоемкий и достаточно опасный процесс, и в этом отношении работа с математической моделью менее затратная и более безопасная.

Решение задачи математического моделирования в данной работе относится к прикладной области исследований и позволяет получить динамику развития опасных факторов пожара (далее ОФП) в различных условиях эксперимента. Как известно, к опасным факторам пожара, воздействующим на людей и имущество, относятся:

1. пламя и искры;

2. тепловой поток;

3. повышенная температура окружающей среды;

4. повышенная концентрация токсичных продуктов горения и термического разложения;

5. пониженная концентрация кислорода;

6. снижение видимости в дыму.

Процесс горения различных веществ имеет некоторые общие закономерности, однако, может кардинально различаться по динамике развития, а также по факторам пожара, поэтому для огневых испытаний извещателей были утверждены несколько наиболее характерных моделей, с помощью которых и проводятся огневые испытания. Нормативные требования [1] предусматривают шесть видов тестовых очагов пожара с разнообразными характеристиками.

Таблица 1

Характеристики тестовых очагов пожара

Цель данной работы заключается в построении математических моделей наиболее характерных очагов пожара, а также в выявлении характерных особенности динамики развития пожара в начальной стадии.

Существует несколько основных моделей пожара используемых для прогнозирования ОФП:

• Интегральная модель;

• Зоннная модель;

• Полевая дифференциальная модель.

Интегральная модель пожара позволяет получить информацию о средних значениях параметров среды в помещении для любого момента развития пожара. Зонная модель позволяет получить представление о размерах характерных зон, возникающих при пожаре в помещении, а также о средних параметрах состояния среды внутри этих зон. И наконец, полевая дифференциальная модель позволяет рассчитать для любого момента развития пожара значение всех локальных параметров состояния в любой точке пространства помещения. Все три модели в математическом отношении характеризуются различным уровнем сложности. Наиболее просто реализуемой является интегральная модель, она же является и наименее точной. Наиболее перспективной, с точки зрения, практического применения является полевая модель горения. Полевые модели основываются на системе дифференциальных уравнений в частных производных. Результатами решения данной системы уравнений являются поля распределения температур, скоростей, концентраций компонентов газовой среды в каждый момент времени.

Программа FDS (Fire Dynamics Simulator) реализует вычислительную гидродинамическую модель (CFD) тепломассопереноса при горении. FDS решает уравнения Навье-Стокса для низкоскоростных температурно-зависимых потоков. Базовым алгоритмом является определенная схема использования метода предиктора-корректора второго порядка точности по координатам и времени. Турбулентность выполняется с помощью модели Смагоринского «Масштабное моделирование вихрей».

Главным образом нас интересует начальный момент времени пожара, когда срабатывание автоматической пожарной сигнализации еще может привести к выполнению системой своих целевых функций (эвакуация людей, эффективное пожаротушение). Время это относительно мало, и в этот промежуток времени пожар имеет некоторые особенности, позволяющие еще более упростить математическую модель. Основной особенностью данного процесса является отсутствие газообмена помещения с окружающей средой. Поступление воздуха в помещение из окружающей среды отсутствует, и динамика возгорания диктуется исключительно пожарной нагрузкой. Поэтому полевая модель пожара, рассматриваемая в данной работе, носит ограниченный характер по времени и справедлива исключительно в начальный момент развития пожара, пока отсутствует поступление воздуха в помещение, и выполняется ограничивающее условие[2]:

(1)

где - суммарная площадь открытых проемов, м²,

g- ускорение свободного падения, ,

H – высота проемов в помещении, м,

V – объем помещения, м³.

Для работы в программе FDS используется схема одноступенчатой химической реакции, результаты передаются через двухпараметрическую модель доли в смеси. По умолчанию рассчитываются два параметра смеси: массовая доля несгоревшего топлива и массовая доля выгоревшего топлива (т.е. продуктов сгорания). Лучистый теплообмен включен в модель посредством решения уравнения переноса излучения для серого газа и, для некоторых ограниченных случаев, с использованием широкодиапазонной модели. Уравнение решается с помощью «метода конечных объемов» (FVM). Данный метод аналогичен методу конечных объемов для конвективного переноса. На всех твердых поверхностях задаются тепловые граничные условия, плюс данные о горючести материала. Тепло- и массоперенос с поверхности и обратно рассчитывается с помощью эмпирических соотношений, хотя при выполнении прямого численного моделирования (DNS) можно вычислить передачу тепла и массы напрямую.

Основные уравнения математической модели, реализуемой FDS, можно записать в общем виде[3]:

, (2)

, (3)

, (4)

, (5)

гдеплотность, -три компонента скорости капель (частиц),, скорость образования испаряющихся капель (частиц), ускорение свободного падения, параметр учитывающий внешние силы, воздействующие на капли (частицы), ,, , , - энтальпия, , скорость тепловыделения в единичном объеме химической реакции, энергия передаваемая от испаряющихся капель (частиц).

Для примера моделирования рассмотрим тестовый очаг горения ТП-6. Данный очаг имитирует горение жидкости (2000 г. этанола) в стальном поддоне размерами 435 мм х 435 мм. Пожарную нагрузку, в идеологии FDS, целесообразно представить трехслойным пользовательским материалом, состоящим из стали, этанола, а также бетонного основания для учета теплообмена поддона с полом. В свойствах каждого слоя необходимо прописать параметры соответствующие материалам - бетон, сталь, этанол. По условиям моделирования данный очаг располагается в центре помещения размерами 10 м х 6 м, высотой 4 м. Материалом стен и перекрытий выберем бетон. Поскольку жидкое топливо в FDS возгорается одновременно по всей поверхности, дополнительный источник зажигания не требуется. Время моделирования выбирается в соответствии с условием (1). Измерения опасных факторов пожара производится на уровне потолка помещения пятью термопарами, пятью датчиками задымления, а также четырьмя датчиками теплового излучения, установленными на стенах на уровне 2 м.

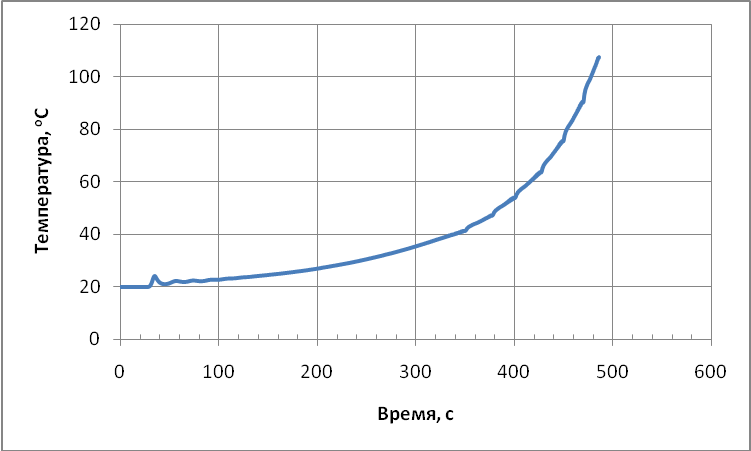
Результаты измерений записываются в табличном виде и для наглядности могут быть представлены в графической форме. На рисунке 1, для примера, показана динамика нарастания температуры для тестового очага пожара ТП-6.

Рисунок 1 – Динамика изменения температуры модельного очага ТП-6.

Результаты математического моделирования динамики опасных факторов пожара, описанные в данной статье, с приемлемой точностью соотносятся с экспериментальными данными, что позволяет говорить об адекватности рассматриваемой математической модели в рамках описанных ограничений.

• Литература:

1. ГОСТ Р 53325-2009. Техника пожарная. Технические средства пожарной автоматики. Общие технические требования. Методы испытаний.

2. Кошмаров Ю.А. Прогнозирование опасных факторов пожара в помещении: Учебное пособие. – М.: Академия ГПС МВД России, 2000. 118 с.

3. Fire Dynamics Simulator (Version 5). Technical Reference Guide. Volume 1: Mathematical Model. National Institute of Standards and Technology. U.S. Department of Commerce. October 29, 2010