В настоящее время, в связи с перегруженностью частотных диапазонов, с увеличением числа естественных помех, а также усложнением вида преднамеренных, исследования в области компенсации помех в каналах радиосвязи приобрели особую важность.
Принцип компенсации помех основан на использовании амплитудно-фазовых различий сигнала и помехи, принятых на пространственно-разнесенные антенны. При сложении смесей, обработанных весовыми коэффициентами, сформированных на основе этих различий, соотношение сигнал/помеха меняется в пользу сигнала.
Широко известным в силу своей простоты и универсальности методом решения задач управления и, в частности, задачи адаптивной подстройки весовых коэффициентов системы компенсации радиопомех, является градиентный метод.
Предположим, что градиент в любой точке на поверхности уровня, образованной среднеквадратической ошибкой (СКО – математическое ожидание квадрата разности выходного и опорного сигналов), может быть точно определен. В этом случае можно применить метод наискорейшего спуска для нахождения точки минимума, то есть таких значений весовых коэффициентов, при которых уровень остатка помехи в выходной смеси будет минимальным.
Метод наискорейшего спуска может быть представлен следующим рекуррентным соотношением:
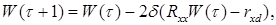(1)
где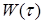 
– вектор весовых коэффициентов, 
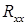– корреляционная матрица, 
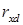– вектор корреляции между входным и опорным сигналами, 
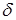– константа, определяющая размер шага; 
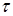– номер шага [1, с. 59].
Метод наискорейшего спуска начинается с предварительного нахождения возможного начального значения минимума на поверхности уровня. Эта оценка представляет собой совокупность исходных значений для каждой из составляющих весового вектора. Выбрав начальное значение, определяют градиент вектора и затем получают следующую оценку, соответствующим образом изменив предыдущее значение. Эта операция заключается в прибавлении к предыдущему значению вектора, имеющего направление, обратное направлению градиента (то есть в направлении наибольшего уменьшения СКО).
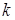
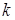
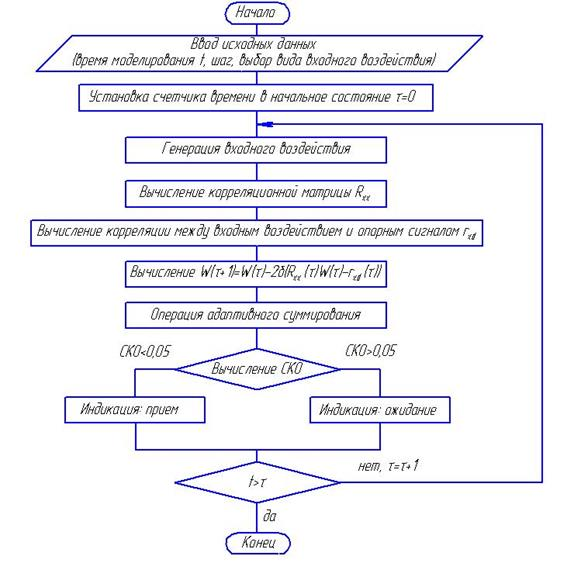
Рис. 1. Блок-схема функционирования компенсатора радиопомех,
построенного на основе алгоритма НС
Блок-схема функционирования компенсатора радиопомех, построенного на основе алгоритма НС, представлена на рисунке 1. Модель, реализующая данную последовательность операций, приведена на рисунке 2. В его левой части изображены блоки, отвечающие за формирование корреляционной матрицы и вектора взаимной корреляции полезного сигнала с опорным. Коэффициентом усиления можно регулировать размер шага, а следовательно, и скорость адаптации. Коэффициент усиления выбирается из интервала от нуля до некоторого значения, зависящего от распределения собственных значений корреляционной матрицы. Необходимо помнить, что при слишком большом размере шага алгоритм становиться неустойчивым. После вычисления весовых коэффициентов по формуле (1) вычисляется произведение этих коэффициентов на входные воздействия. Затем полученные результаты складываются, таким образом, формируя выходной сигнал. Он представляет собой сумму полезного сигнала и некоторой ошибки, которую по тем или иным причинам не удалось скомпенсировать. В правой части рисунка размещены блоки, отвечающие за формирование входных воздействий, а также осциллограф и спектроскопы, необходимые для просмотра полученных результатов.
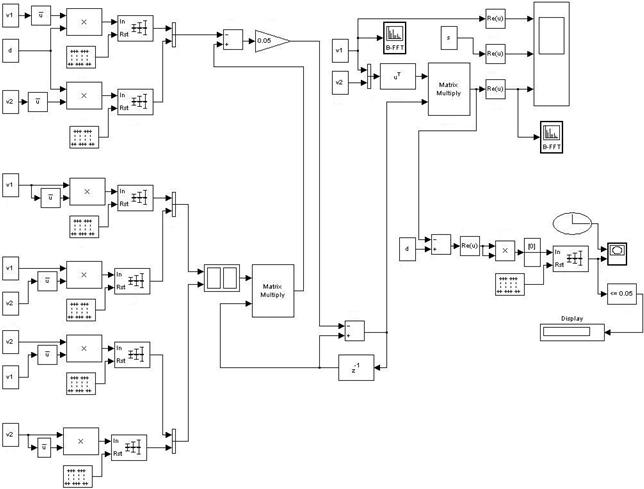
Рис. 2. Модель компенсатора радиопомех, построенного на основе алгоритма НС
Данная модель была создана с целью исследования эффективности подавления помех в ДКМВ канале компенсатором для транкинговой радиосвязи. Некоторые помехи, которые могут присутствовать в эфире, сведены в таблицу 1. С учетом этого были созданы в среде МАТЛАБ генераторы следующих разновидностей входных смесей полезного сигнала и помехи:
- импульсная помеха и АМ-сигнал (амплитудно-модулированный сигнал);
- импульсная помеха и ЧТ-сигнал (частотная телеграфия);
- импульсная помеха и ОФТ-сигнал (относительная фазовая телеграфия);
- узкополосная помеха и АМ-сигнал;
- узкополосная помеха и ЧТ-сигнал;
- узкополосная помеха и ОФТ-сигнал;
- АМ-помеха и АМ-сигнал;
- АМ-помеха и ЧТ-сигнал;
- АМ-помеха и ОФТ-сигнал;
- ЧТ-помеха и АМ-сигнал;
- ЧТ-помеха и ЧТ-сигнал;
- ЧТ-помеха и ОФТ-сигнал;
- ОФТ-помеха и АМ-сигнал;
- ОФТ-помеха и ЧТ-сигнал;
- ОФТ-помеха и ОФТ-сигнал.
Таблица 1. Исследуемые виды помех и их источники
|
Вид помехи |
Источник помехи |
|
Импульсная помеха |
гроза, электроустановки и приборы |
|
узкополосная (синусоидальная) помеха |
сигналы от посторонних радиостанций, излучения генераторов высокой частоты |
|
АМ-помеха |
каналы, созданные другими абонентами сети связи |
|
ЧТ-помеха |
|
|
ОФТ-помеха |
Анализ функционирования модели адаптивного компенсатора помех при подаче на его вход смесей приведенных выше показал уверенное подавление исследуемых помех. В качестве примера, на рисунках 3 и 4 изображены осциллограмма и спектрограммы, полученные в результате запуска модели адаптивного компенсатора помех при подаче на ее вход смеси из ЧТ полезного сигнала и узкополосной помехи.
|
|
||||
|
|
|
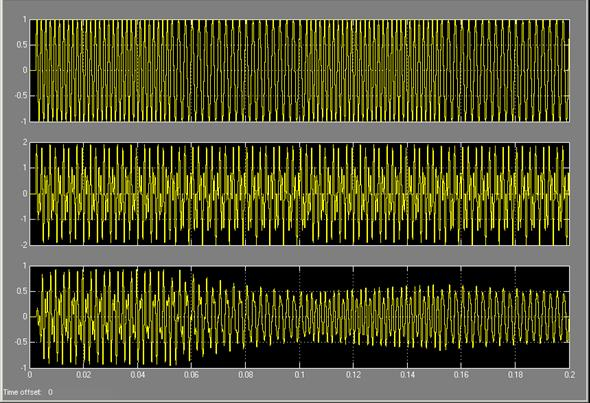
Рис. 3. Осциллограммы, полученные в результате моделирования
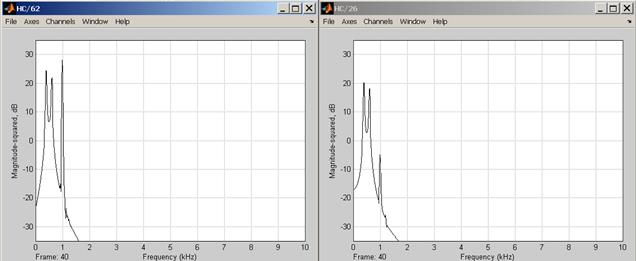
а) б)
|
|
|
а) – для входной смеси (первая антенна);
б) – для выходного сигнала
Созданная модель позволяет оценивать эффективность подавления компенсатором различных видов радиопомех путем анализа спектра, осциллограмм, а также кривой обучения (зависимости уровня СКО от количества итерации). Кроме того, данная модель может быть автоматически преобразована с помощью МАТЛАБ в программу на языке Си, а затем из СИ в машинный код и записана в память микроконтроллера. Таким образом, можно перейти от моделирования к реализации готового изделия с минимальными временными и финансовыми затратами.
Литература
1. Уидроу Б., Стирнз С. Адаптивная обработка сигналов: Пер. с англ. – М.: Радио и связь. 1989. – С. 59.
2. Ануфриев И. Е., Смирнов А. Б., Смирнова Е. Н., Matlab7. – СПб.: БХВ-Петербург, 2005. – 1104 с.
3. Вентцель Е. С. Теория вероятностей, М., 1969. – 576 с.
4. Монзинго Р. А., Миллер Т. У. Адаптивные антенные решетки: Введение в теорию: Пер. с англ. – М.: Радио и связь, 1986. – 448 с.
