В статье рассматривается решение задачи обеспечения помехозащиты каналов системы связи, с помощью адаптивной фильтрации на базе итерационного градиентного метода. Приводится алгоритм работы адаптивного метода, проводится его моделирование. В результате адаптивной обработки приводится спектр аддитивной смеси полезных сигналов и помех, для разных случаев.
Ключевые слова: адаптивная фильтрация, помехозащита, цифровая обработка, широкополосная помеха, спектр сигнала, система связи.
При проектировании различных систем связи, важную роль играет вопрос обеспечения необходимой помехозащиты каналов связи от различного рода помех. Для решения данной задачи рассмотрим применение алгоритма адаптивной фильтрации на базе итерационного градиентного метода, в случае, когда необходимо обеспечить правильный прием узкополосного сигнала при воздействии широкополосной помехи.
Итерационный градиентный метод является одним из первых разработанных методов адаптивной фильтрации, применяемых в антенных решетках. Данный метод обладает важным преимуществом, а именно малая вычислительная сложность, что делает его привлекательным для использования в цифровых системах обработки информации [1, c. 135].
Рассмотрим алгоритм работы данного метода.
Основной идеей градиентного метода является итерационная процедура настройки весового вектора, с помощью которой осуществляется максимизация целевой функции [2, с. 49]:
![]() ,(1)
,(1)
Где W(k) — вектор комплексных весовых коэффициентов адаптивного алгоритма;
μ — постоянный шаг сходимости адаптивного алгоритма;
![]() –градиент по целевой функции в качестве которой берется отношение сигнал/шум;
–градиент по целевой функции в качестве которой берется отношение сигнал/шум;
k — шаг дискретного времени.
Вычислив градиент, учитывая правила дифференцирования, и заменив корреляционную матрицу R на ее выборочную оценку ![]() на k-ом шаге, перепишем уравнение (1):
на k-ом шаге, перепишем уравнение (1):
![]() ,(2)
,(2)
Где x(k)– вектор сигналов адаптивного алгоритма;
α(k) — априорная ошибка моделирования требуемого сигнала.
Далее представлены результаты моделирования работы адаптивной фильтрации. Рассмотрим случай, когда по каналу связи передается один узкополосный сигнала, при воздействии одной широкополосной помехи. Параметры сигналов представлены в таблице 1.
Таблица 1
Параметры сигналов при воздействии одной помехи
|
Тип сигнала |
Частота, кГц |
Мощность, дБ |
|
Полезный |
35 |
13 |
|
Помеха |
- |
29 |
На рисунках 1 и 2 представлены спектры полезного узкополосного сигнала и широкополосной помехи соответственно.
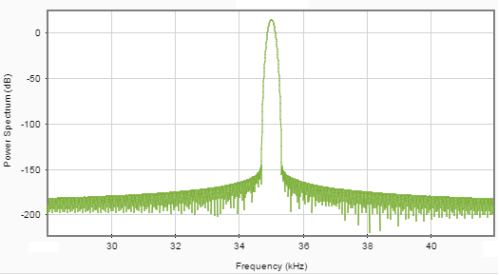
Рис. 1. Спектр полезного сигнала
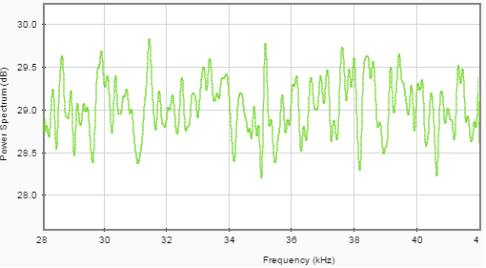
Рис. 2. Спектр широкополосной помехи
На рисунке 3 представлен спектр аддитивной смеси полезного сигнала и помехи.
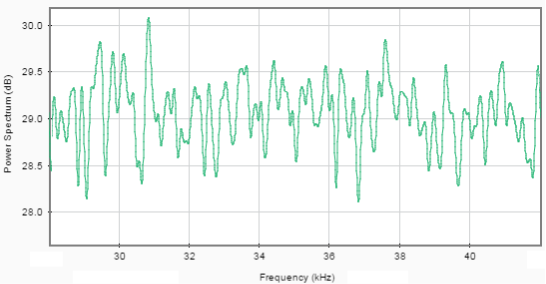
Рис. 3. Спектр аддитивной смеси полезного сигнала и помехи
Из рисунка 3 видно, что полезный сигнал скрывается в полосе частот широкополосной помехи. Применим алгоритм адаптивной фильтрации и посмотрим на результаты.
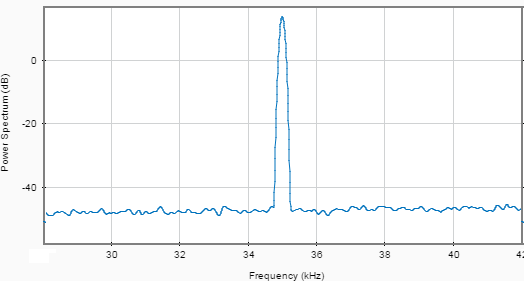
Рис. 4. Спектр аддитивной смеси полезного сигнала и помехи после адаптивной фильтрации, при воздействии одной помехи
Анализируя рисунок 4 видно, что после процесса адаптивной фильтрации отношение сигнал-помеха более чем плюс 40 дБ, в то время как до адаптивной фильтрации минус 16 дБ.
Теперь рассмотрим случай, когда имеем два узкополосных сигнала, при воздействии трёх широкополосных помех, параметры сигналов представлены в таблице 2.
Таблица 2
Параметры сигналов при воздействии одной помехи
|
Тип сигнала |
Частота, кГц |
Мощность, дБ |
|
Полезный 1 |
35 |
13 |
|
Полезный 2 |
30 |
8 |
|
Помеха 1 |
- |
29 |
|
Помеха 2 |
- |
41 |
|
Помеха 3 |
- |
33 |
На рисунках 5 и 6 представлены спектры аддитивной смеси полезных сигналов и аддитивной смеси широкополосных помех.
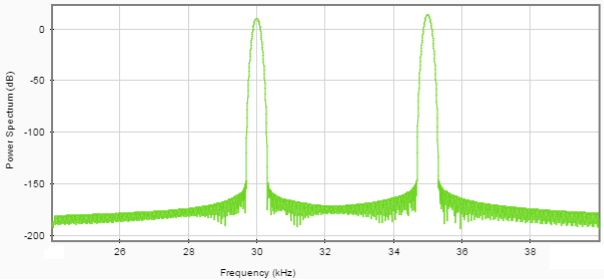
Рис. 5. Спектр аддитивной смеси полезных сигналов
На рисунке 7 представлен спектр аддитивной смеси полезных сигналов и помех. Так же, как и в случае с одной помехой, сигналы скрываются в полосе частот помех. Выполним алгоритм адаптивной фильтрации, результат представлен на рисунке 8.
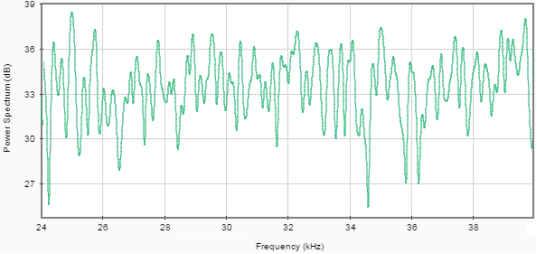
Рис. 6. Спектр аддитивной смеси широкополосных помех
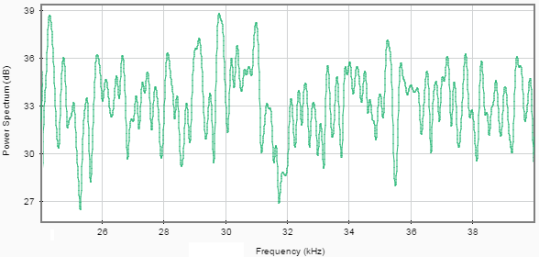
Рис. 7. Спектр аддитивной смеси широкополосных помех
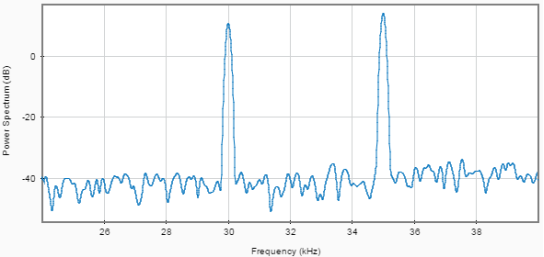
Рис. 8. Спектр аддитивной смеси полезного сигнала и помехи после адаптивной фильтрации, при воздействии трёх помех
Анализируя рисунок 8 видно, что в случае воздействия трёх помех, отношение сигнал-помеха после адаптивной обработки более 40 дБ.
В данной работе были рассмотрены два случая аддитивной смеси полезных сигналов с помехами, входе которых продемонстрирован процесс адаптивной фильтрации помех на базе итерационного градиентного метода. Удалось получить спектры смеси сигналов и помех после адаптации, с помощью которых можно убедиться в решении задачи помехозащиты.
Литература:
- Джиган В. И. Адаптивная фильтрация сигналов: теория и алгоритмы. — М.: Техносфера, 2013. — 528 с.
- Ратынский М. В. Адаптация и сверхразрешение в антенных решетках. — М.: Радио и связь, 2003. — 200 с.

