В настоящее время сильно возросло количество беспроводных устройств, многие из которых работают без связи друг с другом, но в одном частотном диапазоне. Каждое такое устройство является источником помех для других.
Использование антенных решеток позволяет подавлять мешающие сигналы, приходящие с отличных направлений от прихода полезного сигнала[1]. Это выполняется за счет формирования диаграммы направленности(ДН). Существует несколько известных алгоритмов для формирования диаграмм направленности[3], но нигде не встречается их сравнительная характеристика, чему и посвящены были данные исследования.
Для исследований была выбрана 7-ми элементная решетка (смоделированная в среде MATLAB), расстояние между элементами λ/2(где λ рабочая длина волны).
Расстояние между элементами было выбрано из следующего исследования:
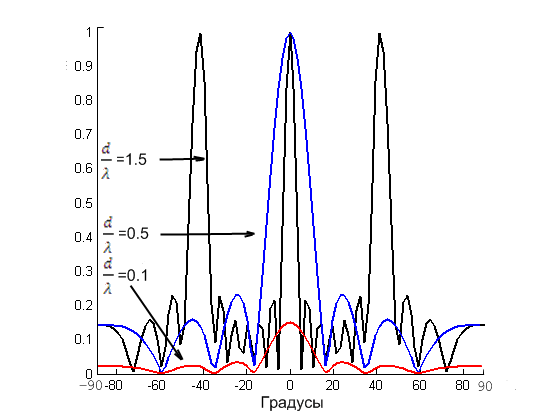
Изменяли, расстояние между элементами антенной решетки от 0 до 2λ с шагом 0,1λ. Полученные результаты приведены на рисунке 1.
Рис.1
При сближении элементов ДН становится практически ненаправленной. А при увеличении отношения расстояния между элементами к длине волны (относительно 0.5) формируются дополнительные максимумы в ДН.
В исследованиях рассматривали 3 алгоритма: Винера-Хопфа[2], минимальной дисперсии[3] и средней квадратичной ошибки[3].
Параметры для прихода помехи и полезного сигнала выбрали следующие:
угол прихода сигнала 45º. Угол прихода помехи 1 от 0º до 45º.Угол прихода помехи 2 от 90º до 45º. Шаг 1º. Получили следующие результаты:
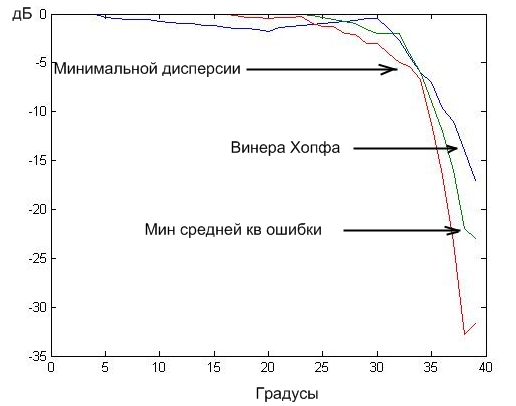
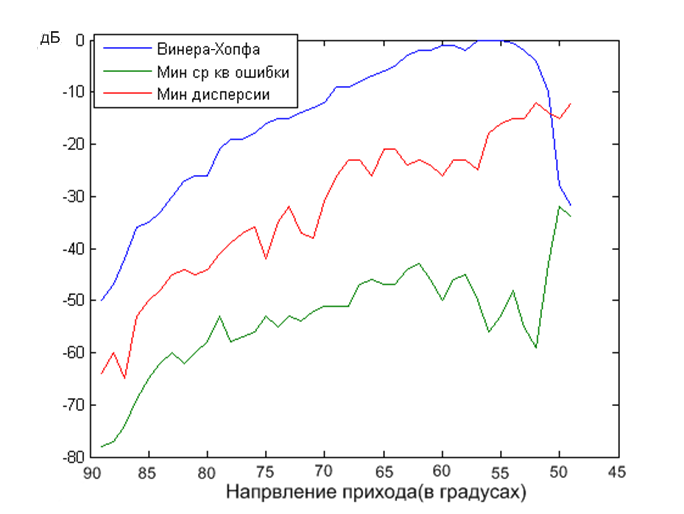
График величины подавления диаграммы направленности с угла прихода полезного сигнала:
Рис.2
Результаты исследований представлены на рисунках 2,3,4,5.
Из графика, представленного на рисунке 2, можно сделать следующие выводы:
При секторе прихода помех более 42º градусов лучше использовать алгоритм минимума средней квадратичной ошибки, так как в этом диапазоне алгоритм позволяет сохранить наименьшее значение подавления полезного сигнала.
При секторе прихода помех менее 42º следует использовать алгоритм Винера-Хопфа, так как уровень подавления полезного сигнала в этом диапазоне наименьший.
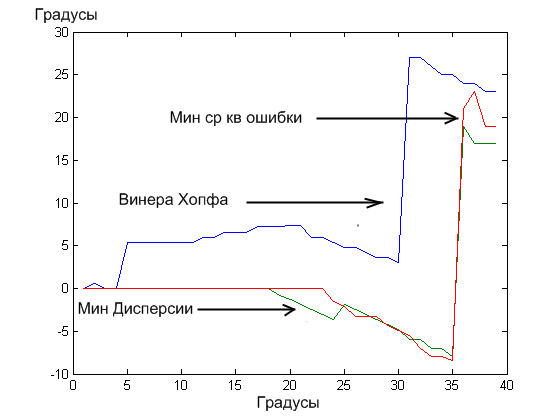
График смещения главного лепестка представлен на рисунке 3.
Рис.3
Выводы, следующие из графика, изображенного на рисунке 3:
Лучше всех себя показал алгоритм минимума средней квадратичной ошибки, так как отклонение главного лепестка началось лишь при секторе направления помех 42°, а полная потеря полезного сигнала при секторе прихода помех 10°.
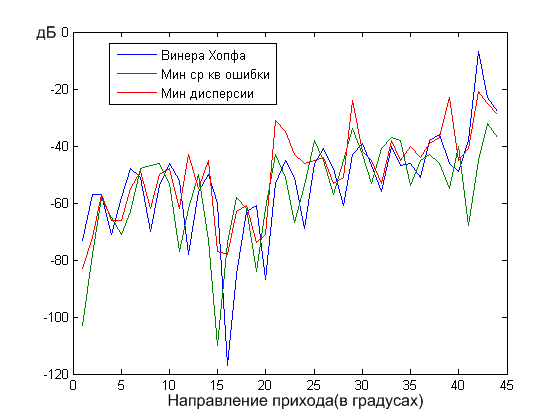
Графики подавления мешающего сигнала (рис. 4 рис. 5):
Рис.4
Рис.5
Выводы по полученным графикам подавления мешающего сигнала:
Из графика на рис. 4 видно, что подавление помехи не равномерно и вид графика приближенно напоминает диаграмму направленности ненаправленной антенной решетки, причем наибольшее подавление в минимумах этой диаграммы.
Из графика на рис. 5 более равномерное, но алгоритм минимума средней квадратичной ошибки оказал большее подавление помехи с угла прихода 90°-45°.
Выводы по исследованиям: В ходе этих исследований наилучшим оказался алгоритм минимизации средней квадратичной ошибки практически по всем показателям. Алгоритм Винера-Хопфа стоит применять, когда сектор прихода помех менее 42°. Алгоритм минимальной дисперсии оказался средним по всем показателям. При заранее известном угле прихода помехи, если есть возможность, следует разместить антенную решетку так чтобы помеха приходила на минимумы ненаправленной диаграммы направленности этой решетки.
Литература:
- Монзинго Р.А., Миллер Т.У. Адаптивные антенные решетки. Введение в теорию / Пер. с англ. В.Г. Челпанова, В.А. Лексаченко. – М.: Радио и связь, 1986.
- Джиган В.И. Плетнева И.Д. Информационные технологии. – М., 2008.
- Воскресенский Д. И., Гостюхин В. Л., Максимов В. М., Пономарёв Л.
- Ross Frank. Smart Antennas for Wireless Communications. 2005.