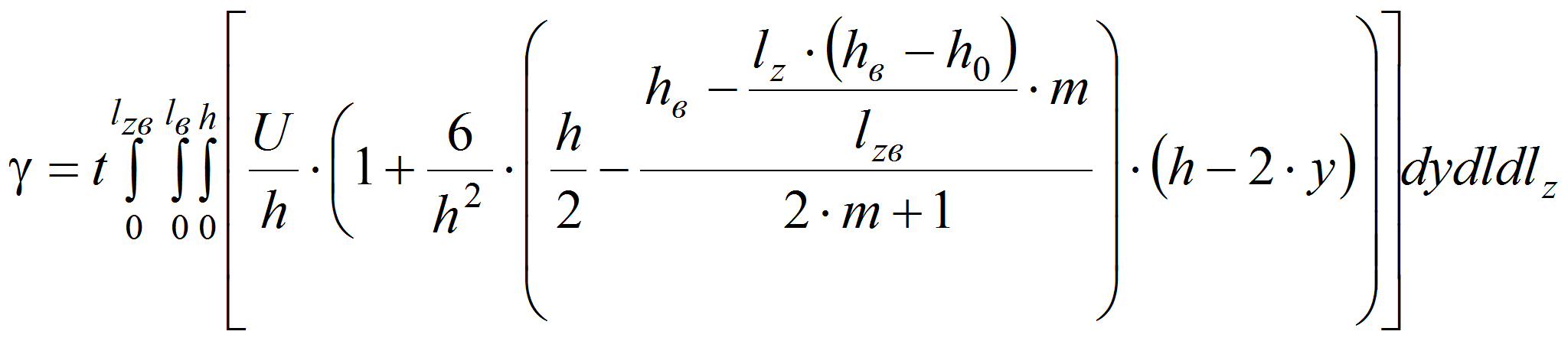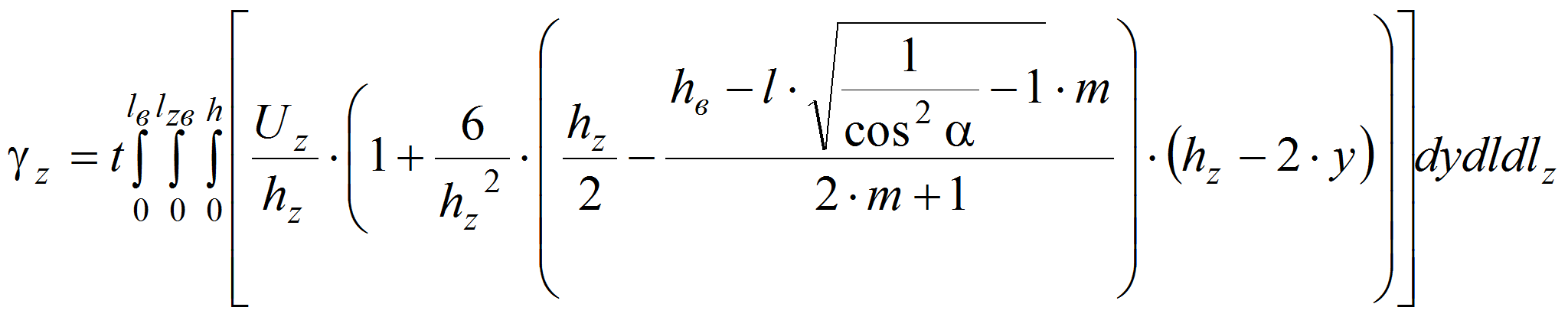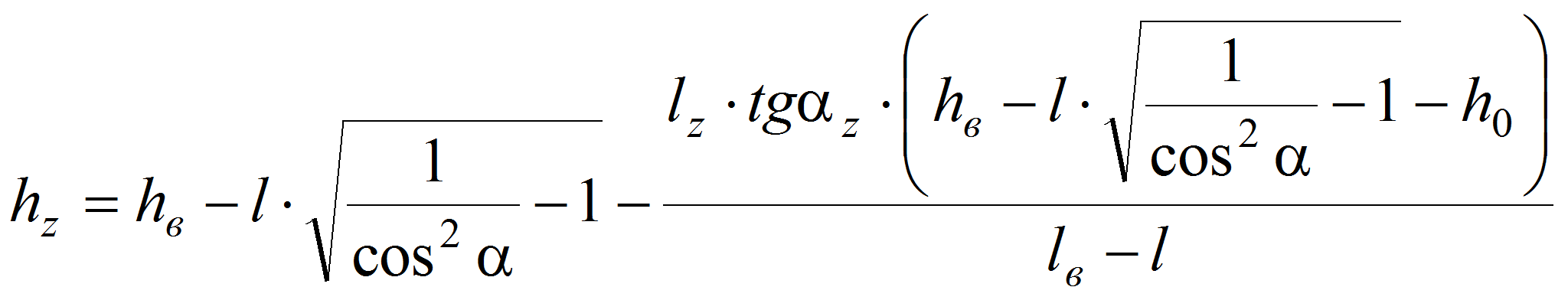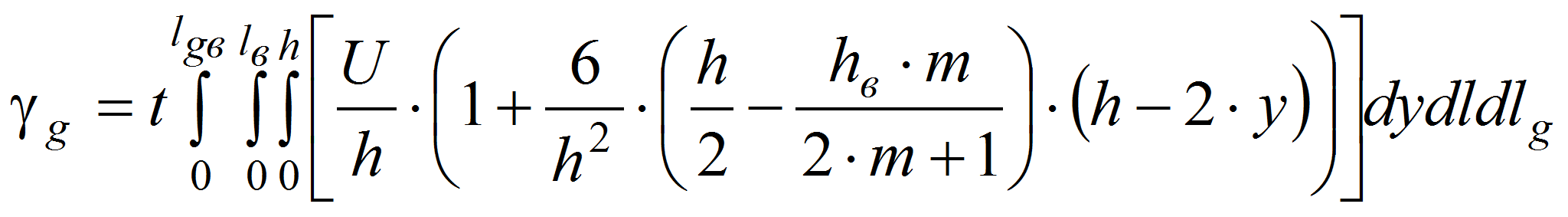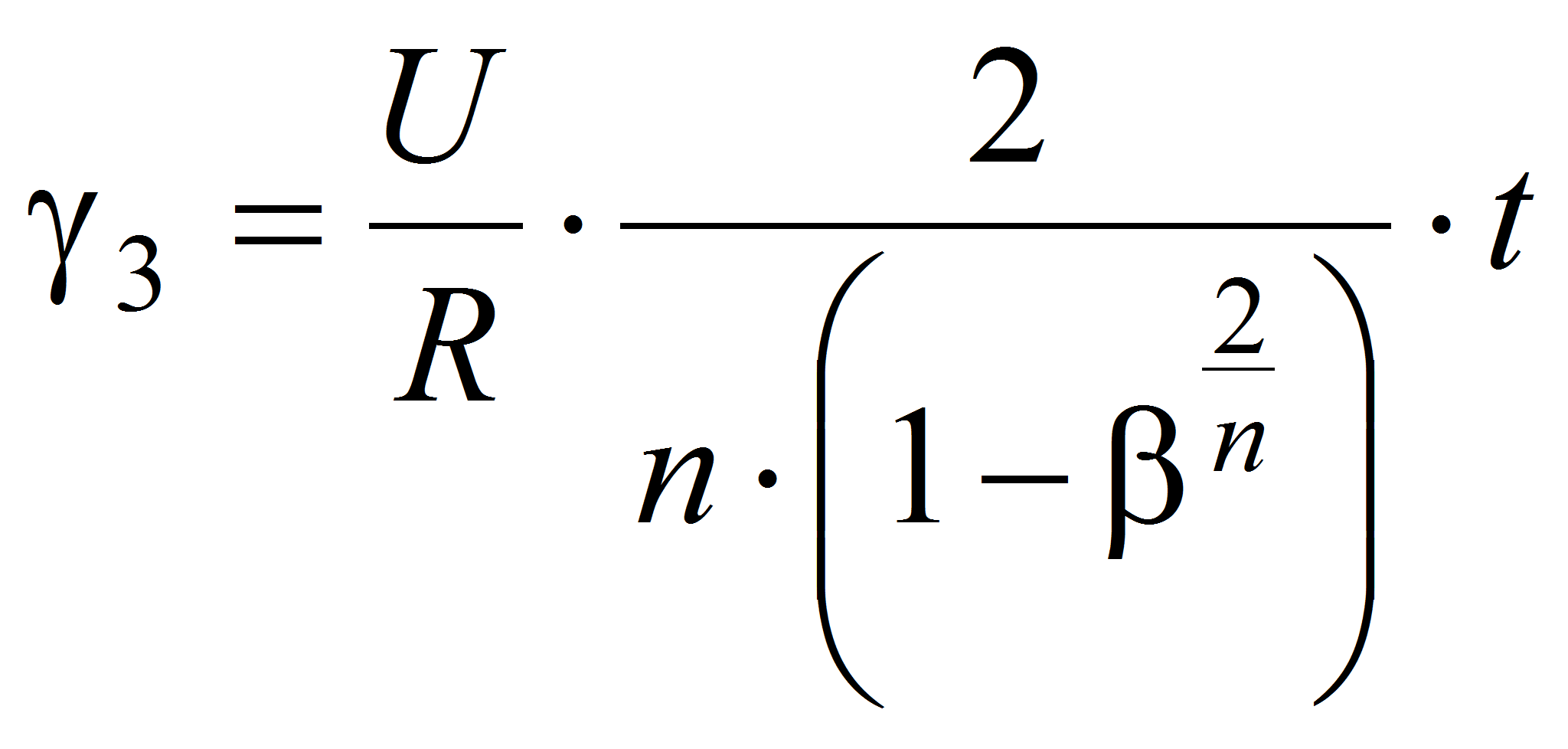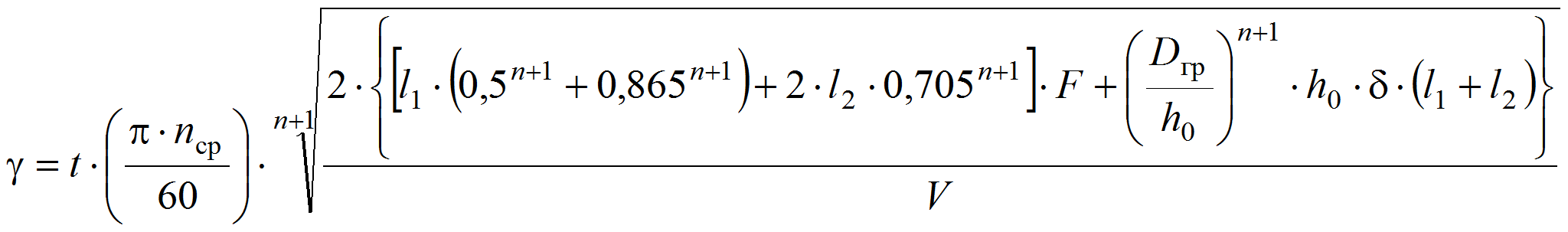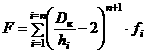Оценить качественные показатели получаемого модифицированного первичного или вторичного термопластичного материала (прочность при разрыве, относительное удлинение при разрыве) можно, используя суммарную сдвиговую деформацию, возникающую в рабочих органах смесителя. Она зависит от различных конструктивных (геометрические размеры рабочих органов смесителя и его габаритов) и технологических (частота вращения роторов смесителя, фрикция, температура внутри смесительной камеры) параметров процесса смешения и диспергирования [1].
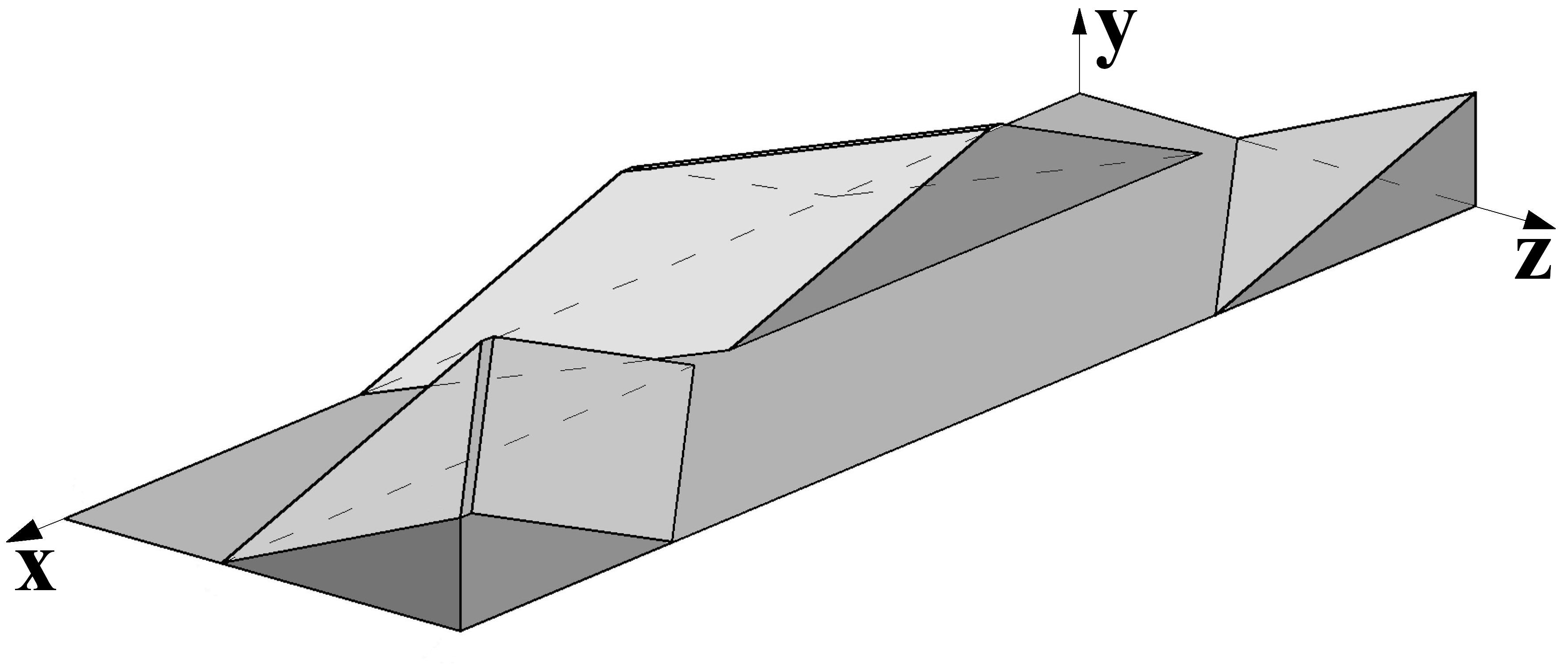
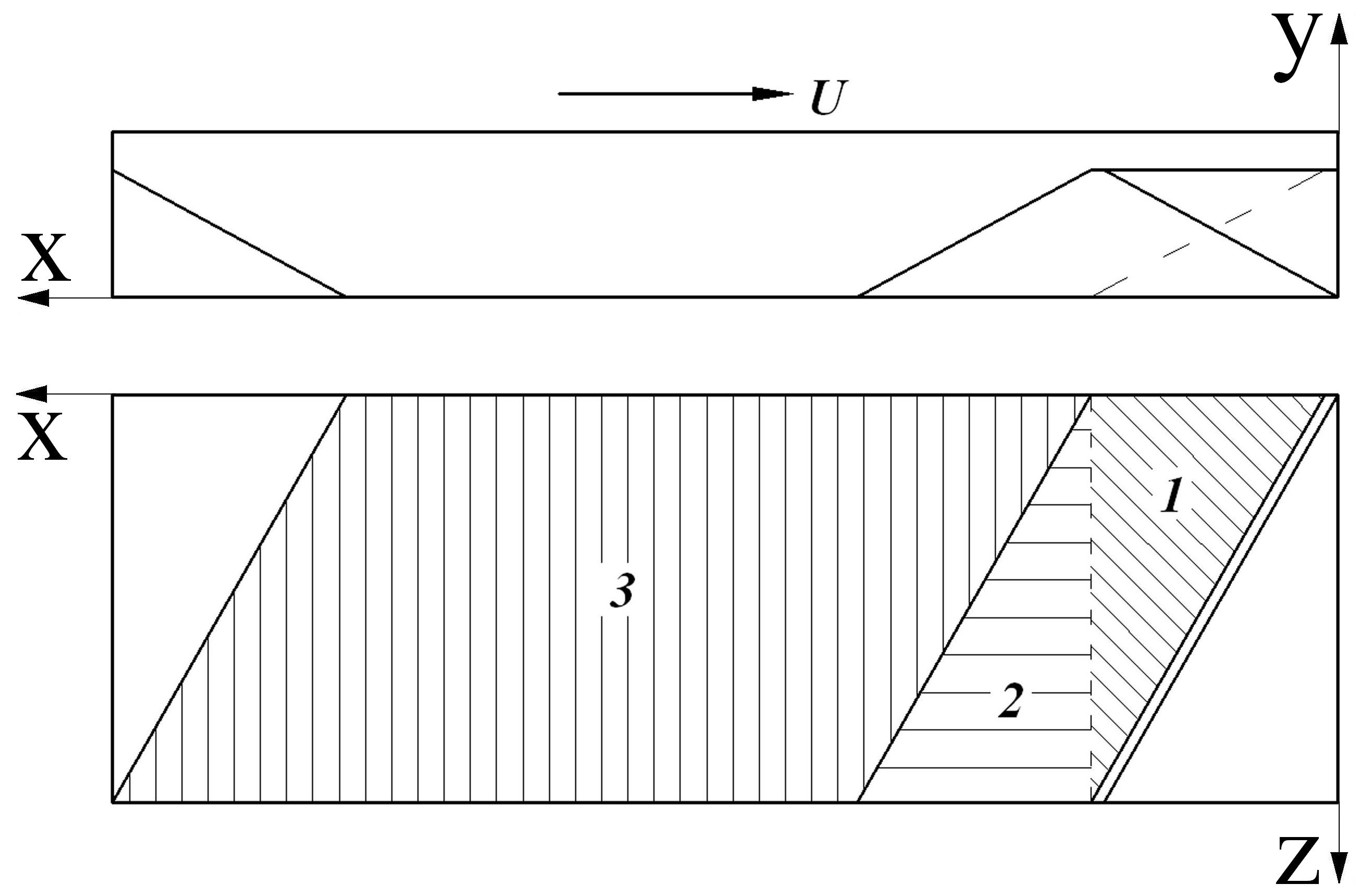
Нами предложены два метода расчёта суммарной деформации сдвига. В первом методе смесительное воздействие может быть рассчитано на основании гидродинамической модели движения материала в сходящемся потоке [2]. Примем допущения, являющиеся традиционными при решении подобных задач: процесс изотермический, ламинарный и установившийся, перерабатываемый материал несжимаем и изотропен, выполняется условие прилипания материала к поверхности роторов и стенкам камеры; осевое перемещение материала в камере смесителя не учитывается. В данном методе делается развёртка ротора относительно оси вращения (рис. 1) и пространство между поверхностью ротора и стенкой камеры разбивается на три зоны различной геометрии (рис. 2). В результате решения задачи были получены следующие зависимости для нахождения суммарной деформации сдвига.
|
Рис. 1 Развёртка двухлопастного ротора |
Рис. 2 Развёртка лопасти ротора – 2 вида (1, 2, 3 – зоны деформирования материала) |
Зона 1: При деформации полимера вдоль оси x получим:
где
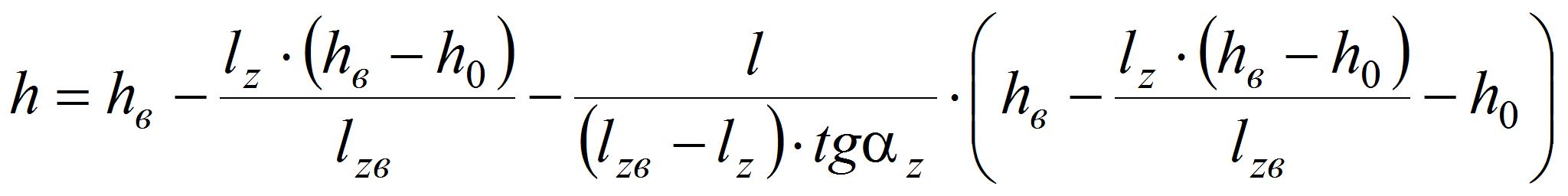 ,
,
![]() ,
lzв
– длина лопасти, αz
– угол наклона винтовой линии,
,
lzв
– длина лопасти, αz
– угол наклона винтовой линии,
В случае движения стенки камеры вдоль оси z:
Результирующая суммарная деформация сдвига в зоне 1 находится по формуле:
Разделив выражение (3) на объём данной зоны получим окончательную формулу для нахождения суммарной деформации сдвига в данной зоне:
Зона 2: В данном случае будет решаться только первая задача из предыдущих двух, т.к. материал в этой зоне не испытывает продольного воздействия, а подвергается деформации только в направлении вращения. Деформация сдвига в направлении вращения ротора выразится в форме уравнения:
Разделив выражение (5) на объём второй зоны получим окончательную формулу для нахождения суммарной деформации сдвига в данной зоне:
Зона 3: Суммарная величина смесительного воздействия, которому подвергается материал в данной зоне за время t, определяется следующим образом [1]:
Величина суммарной деформации сдвига на всей лопасти будет равна алгебраической сумме величин суммарных деформаций сдвига в трёх рассмотренных зонах:
где γ1, γ2, γ3 – величины суммарных деформаций сдвига в зонах лопасти 1, 2 и 3, соответственно.
Для второй лопасти ротора вычисления будут идентичными, изменится только длина лопасти lzв угол наклона винтовой линии αz, в связи с чем изменится скорость движения по оси z и объёмы соответствующих зон V’1 и V’2, а, следовательно, и значения деформаций сдвига в первой и второй зоне – γ1’ и γ2’. Величина суммарной деформации сдвига на всей лопасти будет равна:
где γ1’, γ2’, γ3 – величины суммарных деформаций сдвига в зонах лопасти 1, 2 и 3, соответственно.
Чтобы найти деформацию, приходящуюся на всю длину рабочей части
ротора, необходимо учитывать относительный расход материала,
приходящийся на каждую лопасть. Для этого введём коэффициенты:
![]() и
и
![]() ,
где lzв
– длина первой лопасти, l’zв
– длина второй лопасти, lro
– длина ротора. В результате получим:
,
где lzв
– длина первой лопасти, l’zв
– длина второй лопасти, lro
– длина ротора. В результате получим:
Таким образом, на втором роторе величина суммарной деформации сдвига будет находиться таким же способом, как и на первом, изменится только величина скорости: U2 = f·U, где f – фрикция. Формула для нахождения величины суммарной деформации сдвига на втором роторе:
В итоге, для нахождения величины суммарной деформации сдвига действующей на материал во время процесса смешения и диспергирования во всём объёме смесительной камеры необходимо суммировать величины полученных деформаций сдвига на каждом роторе, используя при этом коэффициент, учитывающий объёмный расход, приходящийся на каждый ротор, и перекрытие зон деформации:
где q – коэффициент, учитывающий объёмный расход, приходящийся на каждый ротор, и перекрытие зон деформации.
Во втором методе за основу взята модель определения мощности привода смесителя через среднюю скорость сдвига, возникающую в материале между кромкой лопасти и стенкой камеры [3].
Была получена следующая зависимость для нахождения суммарной деформации сдвига:
где V – объём перерабатываемой смеси, см3; n – индекс течения, nср – средняя частота вращения заднего и переднего ротора, об/мин; l1 и l2 – длина длинного и короткого гребней ротора, см; Dгр – диаметр гребня ротора по кромке, см; F – коэффициент; h0 – зазор между кромкой гребня ротора и камерой, см; δ – ширина кромки, см.
где i – число элементов, на которые разбивается деформируемый объём или ширина зоны деформации материала, в зазоре между ротором и камерой; Dк – внутренний диаметр камеры смесителя, см; hi – зазор между гребнем ротора и камерой для i-ого элемента, см; fi – площадь сечения i-ого элемента, см2.
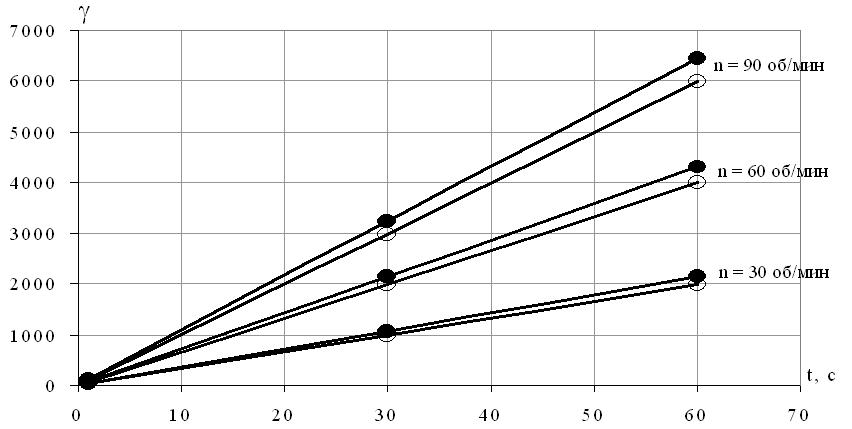
Рис. 3 Зависимость суммарной деформации сдвига от времени процесса смешения
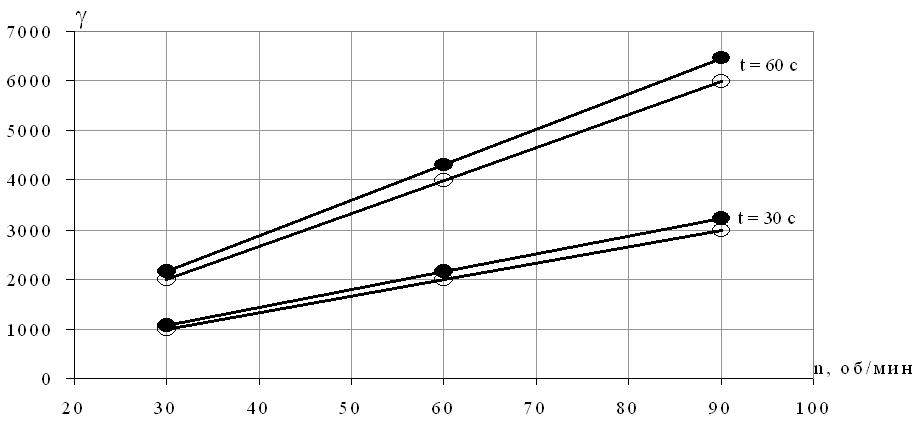
На оба метода разработаны программы расчёта на ЭВМ [4]. По результатам работы программ построены графические зависимости и проведён сравнительный анализ. Оба метода показали сходимость при изменении соответствующих параметров. Выявлено, что расхождение между методами составляет 3,3 % (рис. 3, рис. 4), и изменение в методах какого-либо одного параметра при прочих неизменных не влияет на это расхождение, за исключением величины минимального зазора h0.
Рис. 4 Зависимость суммарной деформации сдвига от частоты вращения рабочих органов смесителя
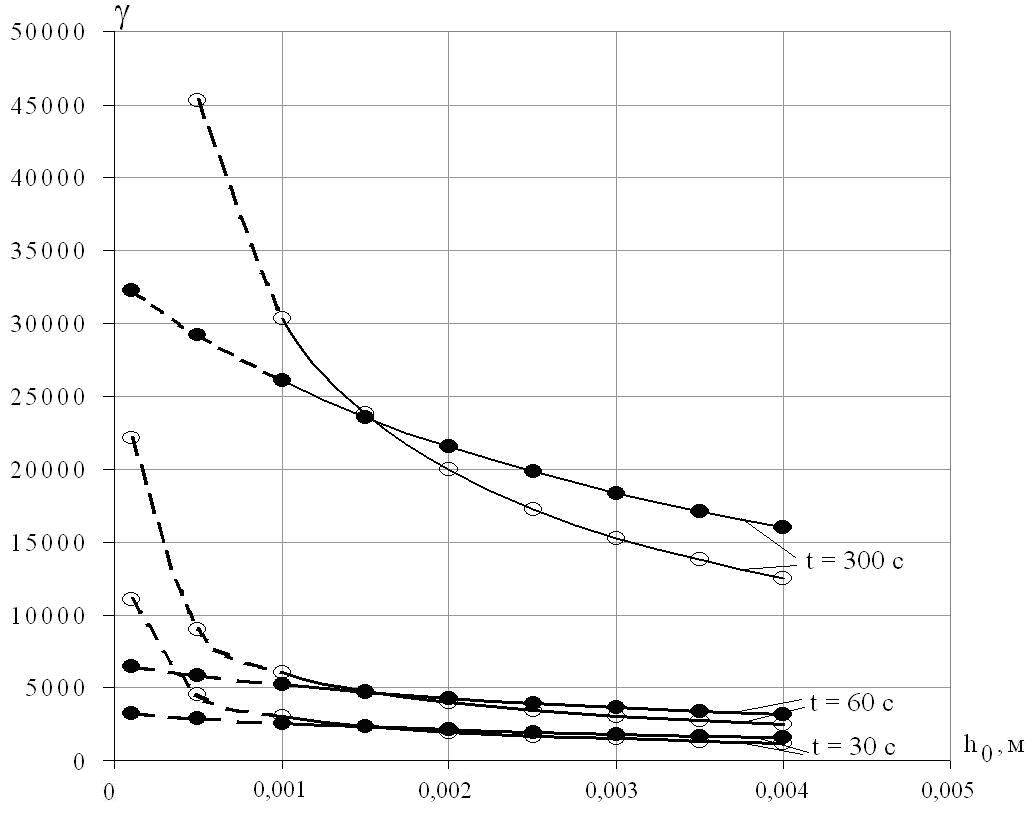
Установлено, что при прочих равных параметрах (nср = 75 об/мин; Dк = 4,78 см; l1 = 4,5 см; l2 = 2,6 см; l = 6,5; V = 100см3; n = 0,3) (рис. 5) на расхождение в моделях оказывает значительное влияние величина минимального зазора между стенкой камеры и кромкой ротора h0. Это расхождение становиться наиболее интенсивным в областях, где h0 < 1 мм (пунктирная линия рис. 5). Но известно, что для двухроторных смесителей с овальными рабочими органами процессы, проходящие при таких величинах минимального зазора, являются не реальными, что говорит о том, что оба метода пригодны для определения критерия качества получаемого материала – суммарной деформации сдвига. Максимальное расхождение составляет не более 15 %.
Рис. 5 Зависимость суммарной деформации сдвига от минимального зазора за время t
Работа выполнена в рамках ФЦП № 14.740.11.0141 по теме “Проведение научных исследований коллективами научно-образовательных центров в области многофункционального приборостроения для промышленных систем управления”.
Литература:
- Методика определения интегрального критерия качества в зонах деформации смесительных устройств / Гуреев С.С., Клинков А.С. // Вестник ТГТУ. Т. 16, №4, 2010. с. 905 - 909.
- Смешение полимеров / Богданов В.В., Торнер Р.В., Красовский В.Н., Регер Э.О. – Л.: Химия, 1979. 192 с.
- Оборудование для переработки пластмасс. Справочное пособие. Под ред. В.К. Завгороднего. М., «Машиностроение», 1976. – 407 с.
- Свидетельство о государственной регистрации программы для ЭВМ. - № 2011612497. Расчет интегрального критерия качества в зонах деформации двухроторных смесителей / С.С. Гуреев, П.В. Макеев, Д.Л. Полушкин, А.С. Клинков, М.В. Соколов; Тамб. гос. техн. ун-т. – № 2011610879 заявл. 14.02.2011. Зарегистрировано 25.03.2011.