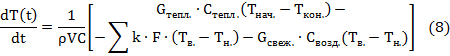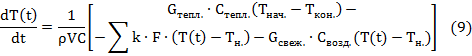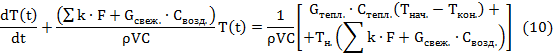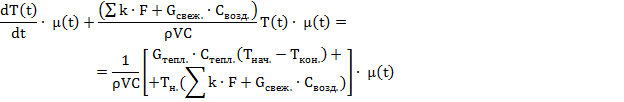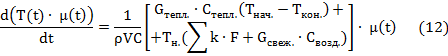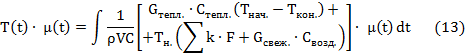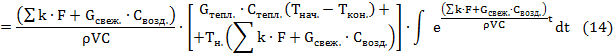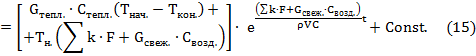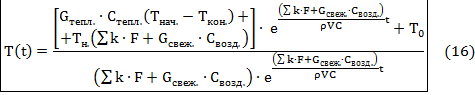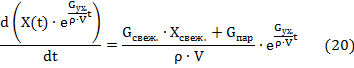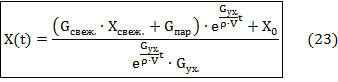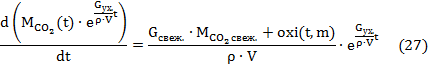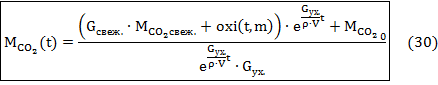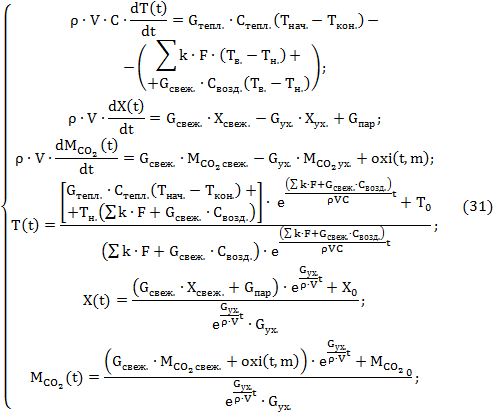Важнейшей стадией исследования алгоритмов управления технологическими объектами является разработка модели объекта, которая отражает происходящие процессы в объекте. Типовые решения по управлению объектами основаны на простейших моделях, оперирующих абстрактными параметрами. Такие модели, в связи с абстрактным характером параметров, не дают возможности глубокого изучения и изменения характеристик объекта. Для более глубокого исследования и синтеза систем автоматического управления представляют интерес модели, раскрывающие физические основы работы объекта.
Классифицируем существующие модели микроклимата теплиц на два типа:
1. Принципиальные модели, использующие данные о физических процессах тепло- и массообмена, происходящих в теплице. Процессы описываются дифференциальными уравнениями с параметрами, имеющими физическую интерпретацию.
2. Кибернетические, когда микроклимат теплицы рассматривается как «черный ящик», и изучается взаимосвязь входных и выходных величин. Параметры этих моделей определяются экспериментально, методом идентификации.
На сегодняшний день существует множество работ, посвященных моделям микроклимата теплиц. Все эти модели берут в основу процесса вегетации фотосинтез.
Отличительной особенностью грибных теплиц от традиционных является сам процесс вегетации, который протекает с выделением тепла, воды и углекислого газа в воздух теплицы. Данная особенность возникает в связи с тем, что грибы являются аэробными микроорганизмами, что предполагает выделение углекислого газа в течение своего развития, в отличие от поглощения последнего растениями в процессе фотосинтеза. В связи с этим возникает необходимость переработки типовых моделей микроклимата теплиц, где в основе процесса вегетации взят фотосинтез.
Модель микроклимата, предложенная в [1], выступает в качестве основы для разработки модели микроклимата грибной теплицы. В данной работе использована принципиальная модель в непрерывном времени.
Модель разработана на основе следующих упрощающих допущений:
1. Модель интерпретирует теплицу как заданный объем воздуха, ограниченный стенами, крышей и основанием. Пространственное распределение переменных, описывающих микроклимат, не учитываются.
2. Изменение биомассы плодовых тел грибов в процессе их развития не учитывается. Биомасса плодовых тел грибов является постоянным значением.
3. Объект управления рассматривается как квазистационарный.
Уравнение теплового баланса энергии, влияющей на изменение температуры воздуха внутри теплицы имеет вид:
, (1)
где 
– плотность воздуха (
);
– объем воздуха (
);
– удельная теплоемкость воздуха (
);
– температура воздуха внутри теплицы (град);
– тепловые поступления от системы обогрева (Вт);
– теплопотери через ограждающие конструкции здания (Вт);
– теплопотери на обогрев свежего воздуха (Вт);
Раскроем члены уравнения (1).
Тепловые поступления от системы обогрева по [3]:
,
(2)
где 
– расход теплоносителя (кг/с);
– удельная теплоемкость теплоносителя ();
,
– температура теплоносителя на входе и выходе теплообменника
(град);
– перепад температур
теплоносителя на входе и выходе теплообменника (град).
Тепловые потери через ограждающие конструкции здания [3, с.47]:
, (3)
где 
– коэффициент теплопередачи ограждающей конструкции (Дж/(
с
));
F
– площадь ограждения (
);
– температура воздуха внутри здания (град);
– температура воздуха наружная (град);
– перепад температуры воздуха (град).
Теплопотери на обогрев свежего воздуха [3]:
, (4)
где 
-
расход свежего воздуха для вентиляции помещения (кг/с);
-
удельная теплоемкость воздуха (Дж/кг
град);
– температура воздуха внутри здания (град);
– температура воздуха наружная (град).
Запишем уравнение (1) полностью, подставив раскрытые члены (2), (3) и (4):
,
(5)
Уравнение массового баланса воды в атмосфере теплицы будет иметь вид:
где
– плотность воздуха (
);
– объем воздуха (
);
– абсолютная
влажность воздуха в атмосфере теплицы (
);
– расход свежего
воздуха (кг/с);
– абсолютная
влажность свежего воздуха ();
– расход уходящего
воздуха (кг/с);
– абсолютная
влажность уходящего воздуха ();
– расход пара (кг/с).
Уравнение массового баланса [2, с.81]углекислого газа в атмосфере теплицы определяется из баланса масс углекислого газа следующим образом:
где
– плотность воздуха ();
– объем воздуха ();
– абсолютное
содержание CO2
в атмосфере теплицы (
);
– расход свежего
воздуха (кг/с);
- абсолютное содержание CO2
в атмосфере (
);
- расход уходящего воздуха
(кг/с);
- абсолютное содержание CO2
в уходящем воздухе из теплицы ();
– процесс окисления
грибами воздуха, сопровождаемый выделением CO2
в воздух теплицы (
).
Для получения значений температуры, влажности и содержания углекислого газа на основании разработанных уравнений выразим эти значения из дифференциальных уравнений.
Запишем уравнение температуры в дифференциальной форме (5):
Примем температуру
уходящего воздуха за температуру воздуха внутри помещения (
).
Тогда уравнение примет вид:
Получили линейное неоднородное дифференциальное уравнение первого порядка. Выразим его:
Определим вспомогательную
функцию
Примем
,
тогда:
Умножим исходное уравнение
(10) на
(11):
Проинтегрируем уравнение (12):
Примем за постоянный
множитель
и вынесем его за знак интеграла, затем умножим обе части уравнения на
:
Возьмем интеграл:
=
Выразим
вместо Const.:
где
– начальная температура.
Получим значение абсолютной влажности. Запишем уравнение влажности в дифференциальной форме (6):
Примем влажность уходящего
воздуха за влажность воздуха внутри помещения (
).
Тогда уравнение примет вид:
Полученное дифференциальное уравнение первого порядка выразим в каноническом виде:
Определим вспомогательную
функцию
Примем
,
тогда:
Умножим исходное уравнение
(18) на
(19):
Преобразуем:
Приняв
проинтегрируем уравнение (20) по t:
Умножим обе части уравнения
на
и возьмем интеграл:
Выразим
,
подставив
вместо Const.:
где
– начальная влажность.
Найдем значение содержания CO2. Запишем уравнение массового баланса углекислого газа в атмосфере теплицы в дифференциальной форме (7):
Примем содержание CO2
уходящего воздуха за содержание CO2
воздуха внутри помещения (
).
Тогда уравнение примет вид:
Выразим полученное дифференциальное уравнение первого порядка:
Определим вспомогательную
функцию
-
Примем
:
Умножим исходное уравнение
(25) на
(26):
Преобразуем:
Примем
и проинтегрируем уравнение:
Умножим обе части уравнения
на
и возьмем интеграл:
Выразим
(t),
подставив
вместо Const.:
где
-
начальное содержание углекислого газа.
Таким образом, система уравнений (46), приближенно описывающая микроклимат теплицы, имеет вид:
Приведенная в этой работе модель (31) приближенно описывает микроклимат теплицы, что допустимо для анализа и синтеза алгоритмов управления. Модель не учитывает распределение параметров микроклимата по площади и высоте тепличного сооружения.
Вывод. Модель позволяет вести расчет задающих воздействий по параметрам микроклимата теплицы, прогнозировать влияние каждого из значений микроклимата на остальные, дает возможность рассчитывать показатели качества управления.
Литература:
Семенов, В.Г. Математическая модель микроклимата теплицы. / В.Г. Семенов, Е.Г. Крушель // Известия ВолгГТУ. – 2009. -№6. – с.32-35.
Олссон, Г. Цифровые системы автоматизации и управления. / Г. Олссон, Д. Пиани. – СПб.: Невский диалект, 2001г. – 557 с.
А.Г. Егизаров. Общая теплотехника, теплоснабжение и вентиляция. Учебник для вузов. – М.: Стройиздат, 1982. – 215 с., ил.
