В статье автор разрабатывает математическую модель движения робота-сборщика космического мусора в космосе, алгоритмы управления движением робота и анализирует полученные результаты.
Ключевые слова: робот, космос, космический мусор.
Робот-сборщик космического мусора движется по геостационарной орбите. Геостационарная орбита — это круговая орбита, которая расположена над экватором Земли, находясь на которой робот-сборщик техногенных объектов обращается вокруг планеты с угловой скоростью, равно угловой скорости вращения Земли вокруг оси.
Для того, чтобы смоделировать маневр между орбитой робота и орбитой нежелательного техногенного объекта, необходимо описать как происходит смена орбиты робота во время преследования нежелательных объектов.
Пусть вокруг Земли (показанной на рис. 1 заштрихованной окружностью) имеются две концентрические круговые орбиты

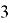

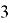
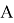
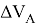
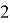
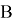
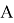
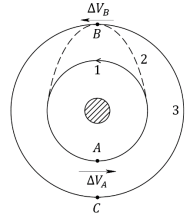
Рис. 1. Переход к требуемой орбите
Если подобрать нужную величину для дополнительной скорости
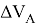
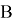
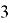
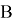
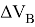
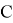
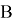
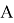
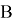
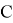
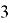
После включения двигателя в точке
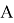
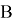
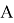
Причем время движения спутника из
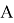
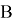
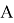

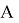
Для того, чтобы смоделировать движение робота за нежелательным космическим объектом, необходимо составить математическую модель движения робота.
Поскольку робот и техногенный объект двигаются по круговой орбите, то необходимо составить модель круговой орбиты для робота и такого объекта. Уравнение эллипса для робота и космического мусора выглядит следующим образом:
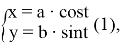
где
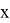
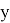
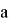
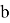
Значения
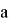
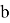
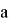
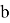
Для моделирования движения робота по орбите, необходимо задать входные данные. В качестве входных данных зададим массу робота, силу тяги и время. Масса робота известна, время задаем вручную.
Расстояние между роботом и нежелательным техногенным объектом находится по формуле:
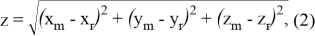
где
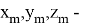
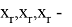
Для того, чтобы правильно оценить значение тяги двигателя, необходимое для достижения цели, можно посчитать скорость робота при заданной массе.
Закон изменения скорости при движении с постоянным ускорением описывается следующим уравнением:
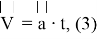
где
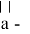
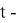
Если проинтегрировать скорость, то получим значение пройденного расстояния
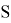
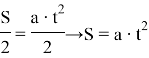
Отсюда очевидно, что мы затрачиваем время
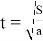
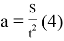
Пусть расстояние до объекта
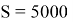
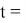
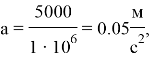
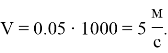
Поскольку робот вылетает из орбитальной станции, уже имея первую космическую скорость (
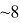
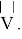
Так как в начале полета робот вместе с выброшенным веществом является замкнутой системой, то реактивная тяга при отсутствии внешних сил:
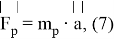
где
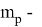
Поскольку масса робота
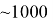
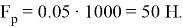
Полученное значение отображает приблизительное значение реактивной тяги двигателя, которое необходимо задать на вход в систему. Помимо этого, можно оценить корректность выбора жидкостного ракетного двигателя, поскольку такой двигатель легко справится с такой тягой.
Тогда математически можно выяснить расстояние и скорость робота. Поскольку первая космическая скорость равна ~8 км/с, то будем считать, что начальная скорость робота равна 8000 м/с. Ускорение робота высчитывается следующим образом:
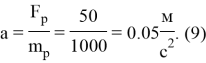
Тогда при
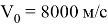
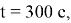
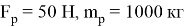
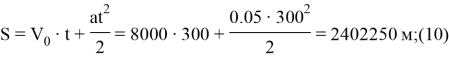
В таком случае максимальная скорость будет равна:
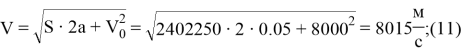
Таким образом, мы получили значения скорости, требуемой роботу для достижения объекта и значение расстояния, которое должен пролететь робот.
Алгоритм работы управления роботом начинается с проверки работоспособности всех систем и наличия топлива робота. Если какая-то система отказала, то оператору на станции выводится сообщение об ошибке. Если все системы в порядке и уровень топлива в норме, то начинается процесс поиска объекта. Лазерный дальномер сканирует местность на наличие нежелательного техногенного объекта и в случае обнаружения начинает расчет оптимальной траектории. После того, как траектория рассчитана, робот рассчитывает, как должна изменяться тяга на протяжении всего пути. После окончания расчетов включается основной двигатель, и робот начинает свое движение. По заранее рассчитанной траектории, роботу сообщается скорость, и он первую половину пути разгоняется, а вторую часть пути тормозит. Как только робот достигает расстояния 5 метров до объекта, основной двигатель отключается, и робот движется с первой космической скоростью как в начале своего пути. Далее происходит проверка основных условий, а именно, проверка объема и веса нежелательного техногенного объекта. В случае, если космический мусор слишком велик или имеет слишком большую массу, то происходит отмена операции, происходит повторная проверка систем и робот снова начинает поиск объектов. В случае, если космический мусор подходит по всем параметрам, то робот стабилизирует свое положение с помощью гироскопической системы, готовясь к дальнейшему захвату. Далее происходит проверка формы объекта. Если объект несложной формы, то происходит автоматический захват объекта и помещение в контейнер для сбора космического мусора, если же объект сложной формы, то оператор удаленно управляет манипулятором и также помещает объект в контейнер. Далее происходит штатная проверка заполнен ли контейнер, если контейнер не заполнен, то происходит проверка работоспособности систем и уровня топлива. В противном случае робот направляется на станцию для смены контейнеров и дозаправку. После этого робот снова отправляется на орбиту и продолжает поиск нежелательных космических объектов.
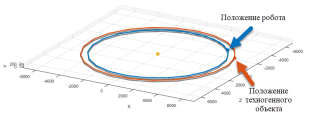
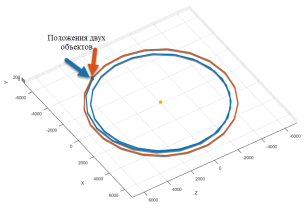
Теперь, когда была составлена математическая модель системы управления, а после были разработаны алгоритмы управления двигателем в системе MATLAB, необходимо проанализировать результаты. При отработке программы, траектория полета робота и нежелательного космического объекта выглядит как показано на рисунке 2.
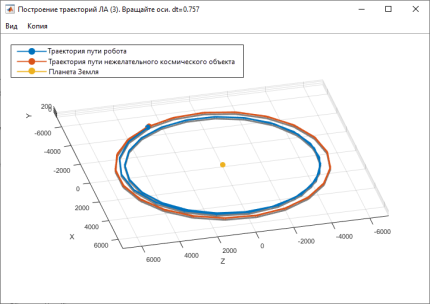
Рис. 2. Траектория движения робота и космического мусора
Разобьем выполнение программы на 4 шага. Отобразим траекторию и графики скорости.
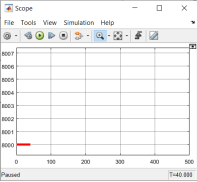
Шаг 1. Робот вылетает, имея первую космическую скорость равную 8 км/с. С такой же скоростью движется нежелательный техногенный объект, однако робот его еще не обнаружил. Траектория движения робота и космического мусора показана на рисунке 3, а график скорости показан на рисунке 4.
|
Рис. 3. Траектория движения робота и космического мусора: шаг 1 |
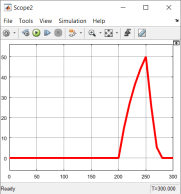
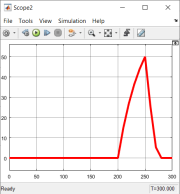
Рис. 4. Скорость робота: шаг 1 |
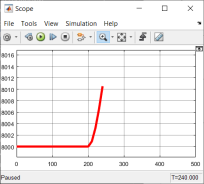
Шаг 2. В заданный момент времени
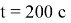
|
Рис. 5. Траектория движения робота и космического мусора: шаг 2 |
Рис. 6. Скорость робота: шаг 2 |
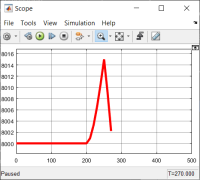
Шаг 3. Робот рассчитал, когда ему нужно ускориться, затормозить и практически догнал нежелательный космический объект. Траектория движения робота и космического мусора показана на рисунке 7, а график скорости показан на рисунке 8.
|
Рис. 7. Траектория движения робота и мусора: шаг 3 |
Рис. 8. Скорость робота: шаг 3 |
Шаг 4. Робот долетел до объекта и его скорость вернулась до первой космической. Теперь робот может на этой скорости захватить объект. Траектория движения робота и космического мусора показана на рисунке 9, а график скорости показан на рисунке 10.
|
Рис. 9. Траектория движения робота и мусора: шаг 4 |
Рис. 10. Скорость робота: шаг 4 |
Таким образом видно, что по формуле (11) график скорости высчитывается верно.
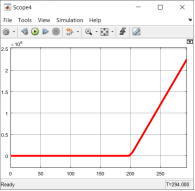
Теперь проанализируем графики ускорения, расстояния и силы тяги. График реактивной тяги показан на рисунке 11. График ускорения показан на рисунке 12. График расстояния показан на рисунке 13.
|
Рис. 11. График реактивной тяги |
Рис. 12. График ускорения |
Рис. 13. График расстояния |
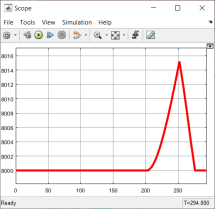
Из графика реактивной тяги видно, что после обнаружения дальномером космического мусора, на 200 секунде робот начнет увеличивать силу тяги, на 230 секунде робот достигнет максимальной силы тяги и на 270 секунде робот снова установит нулевую тягу.
Из графика ускорения видно, что по формуле (9), ускорение высчитывается верно.
Из графика расстояния видно, что по формуле (10), расстояние высчитывается верно.
Литература:
1. Круговая орбита [Электронный ресурс] https://ru.wikipedia.org/wiki/Круговая_орбита. Дата обращения: 31.05.2020
2. Управление движением космических аппаратов [Электронный ресурс] // https://epizodsspace.airbase.ru/bibl/znan/1986/3/3-rau-upr.html. Дата обращения: 04.07.2020