Статья посвящена разработке прототипа манипулятора на гибких связях для работы в труднодоступных средах. В работе представлена математическая модель и приводится решение прямой задачи кинематики для манипулятора с управляемым изгибом. Также дается описание разработанного прототипа и описывается экспериментальное исследование, целью которого являлась проверка правильности математической модели и работоспособности самого манипулятора.
Ключевые слова: манипулятор с управляемым изгибом, математическая модель, прямая задача кинематики.
Введение. В настоящее время использование гибких манипуляторов, имеющих змеевидную форму, способно принести огромную пользу в областях, где использование манипуляторов с жесткими звеньями затруднено или невозможно. Обладая высокой подвижностью и большими значениями коэффициента сервиса, данный класс манипуляторов может применяться для проведения аварийно-спасательных работ или в медицине в области минимально инвазивной хирургии.
Первым шагом в разработке прототипа манипулятора с управляемым изгибом является составление и анализ математической модели, которая будет заложена в основу системы управления. Существуют ряд отечественных [1,2] и зарубежных исследований, описывающие различные кинематические модели манипуляторов с управляемым изгибом. В зависимости от конструктивных особенностей манипуляторов, данные модели имеют свои особенности.
Система управления разработанного манипулятора основана на кинематической модели, предложенной Bryan Jones и Ian Walker [3,4]. Данный подход основан на модификации метода Денавита-Хартенберга. В качестве новых параметров используются длина одной секции
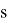
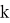
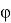
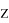
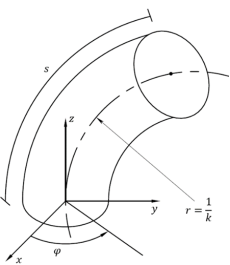
Рис. 1. Переменные манипулятора
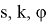
Итоговая матрица преобразования для одной секции манипулятора будет иметь следующий вид:

Решением прямой задачи кинематики для гибкого манипулятора с n- секциями будет являться произведение матриц, соответствующее количеству этих секций:
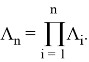
Полученное решение позволяет определить рабочую зону манипулятора, а также получить его конфигурации при заданных параметрах. Моделирование происходит с использованием пакета прикладных программ MatLab и Simulink со значениями длин секций
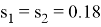
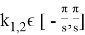
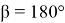
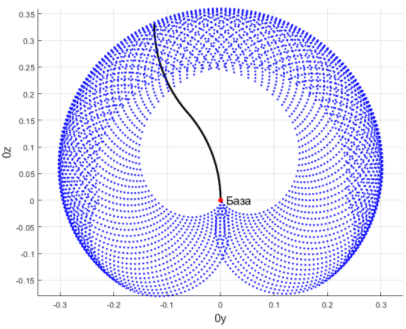
Рис. 2. Рабочая зона двухсекционного манипулятора в плоскости
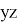
Разработанный манипулятор может применяться для выполнения поисково-спасательных работ. Прототип состоит из двух последовательно соединённых секций, каждая из которых приводится в движение, благодаря использованию трех внутренних тросов, смещенных на 120⁰ относительно друг друга. Приведение движения тросам от двигателя осуществляется с помощью передачи винт-гайка скольжения, стальной направляющей и специальной каретки. В центре проходит полый пружинный трос, который придает необходимую гибкость конструкции. На рисунке 3 представлен разработанный прототип манипулятора.

Рис. 3. Манипулятор на гибких связях
Каждая секция состоит из пяти отдельных элементов, соединённых между собой по средству шарнира Гука (рис.4). Соединение состоит из двух сборных вилок, соединенным крестообразным элементом, образующих кинематические пары с взаимно перпендикулярными осями.
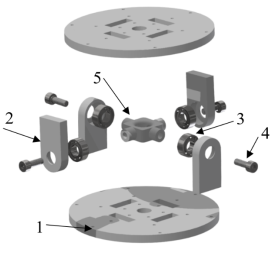
Рис. 4. Разборное соединение сегментов манипулятора
Сегменты (1) имеют наружный диаметр
Основной задачей эксперимента является проверка правильности математической модели и работоспособности самого манипулятора. Результаты эксперимента представлены на рисунках 5,6,7,8.
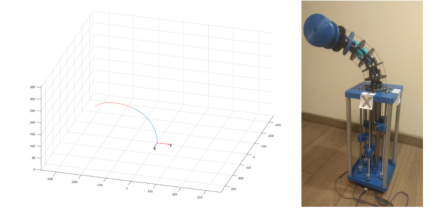
Рис. 5. Конфигурация при
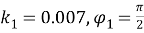
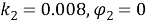
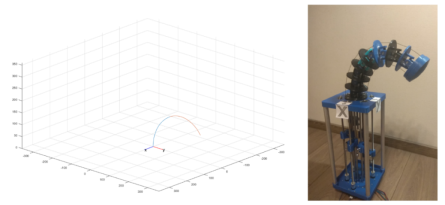
Рис. 6. Конфигурация при
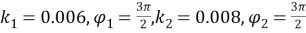
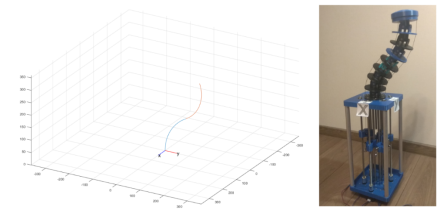
Рис. 7. Конфигурация при
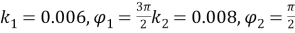
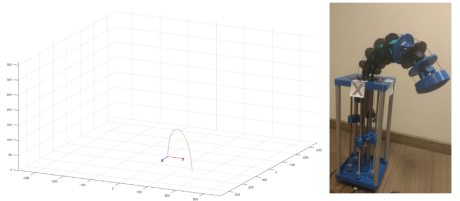
Рис. 8. Конфигурация манипулятора при
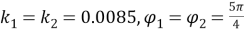
Проведенное экспериментальное исследование позволило подтвердить выбранную математическую модель. Следует отметить, что сильное влияние на движения манипулятора оказывают динамические свойства конструкции гибких секций. Для более корректной работы необходимы дополнительные исследования и доработка гибкой части манипулятора.
Литература:
- Богданов Д. Р., Даринцев О. В. Кинематика манипулятора с управляемым изгибом на базе твердых элементов со сферической поверхностью. Мехатроника, автоматизация, управление. 2015; 16(10): 671–678.
- Семёнов К. Д., Мазунин И. Д., Каменских А. Д., Фищенко П. А., Медяков А. А. Применение основ мехатроники для разработки эффективного манипулятора на основе гибких сочленений // Альтернативные источники энергии в транспортно-технологическом комплексе: проблемы и перспективы рационального использования. 2015. Т. 2. № 2. С. 850–853.
- M. W. Hannan and I. D. Walker, “Kinematics and the Implementation of an Elephant’s Trunk Manipulator and Other Continuum Style Robots”, In: Journal of Robotic Systems, 20(2), 2003, pp. 45–63.
- Jones, B. A. and Walker, I. D. (2006). Kinematics for multisession continuum robots. IEEE Transactions on Robotics, 22(1):43–55.

