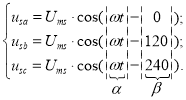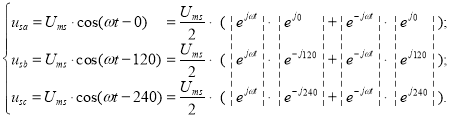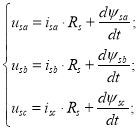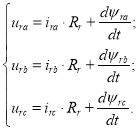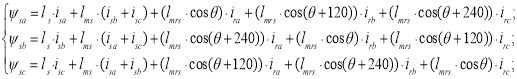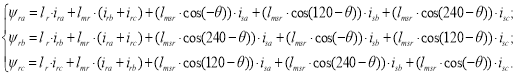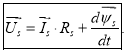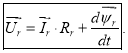При подготовке слайдов для проведения вебинаров возникла необходимость введения дополнительных обозначений при выводе уравнений асинхронного двигателя и сделаны существенные изменения в работе [1].
1. Преобразование мгновенных значений напряжений и токов в степенные функции.
Фазные напряжения в статоре:
|
|
(1) |
Выразим ua, ub и uc через степенные функции по формуле Эйлера:
![]() .
.

Примечание: ![]() .
.
![]()
|
|
(2) |
Мгновенные значения токов статора и ротора:
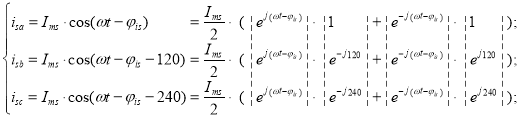
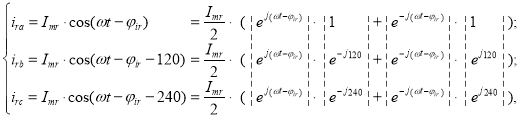
гдеφis и φir – углы отставания от напряжения во времени для фазы «а».
Преобразование углов через степенные функции:
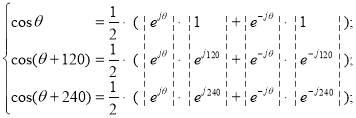
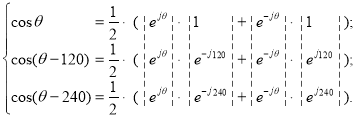
Численные значения ej0, ej120 и ej240:
![]()
![]()
![]()
![]()
![]()
![]()
2. Пространственные векторы напряжения и токов.
Единичные пространственные векторы:
![]()
![]()
![]()
|
|
(3) |
![]()
![]()
![]() .
.
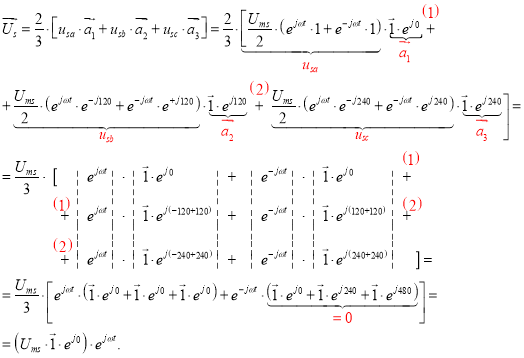
Пространственный вектор напряжения статора ![]() :
:
|
|
(4) |
Вывод: пространственный вектор напряжения статора ![]() имеет такой же угол и модуль комплекса
имеет такой же угол и модуль комплекса ![]() (фазы «а») на временной комплексной плоскости.
(фазы «а») на временной комплексной плоскости.
Геометрический смысл преобразования мгновенных значений напряжений в пространственный вектор показан на рис. 1.
Последовательность построений: во временной системе координат определяются мгновенные значения векторов на действительную ось usa, usb, usc, далее они переносятся на действительную ось в пространственную систему координат в виде отрезков. Затем осуществляется разворот этих отрезков с помощью единичных пространственных векторов. Далее производится геометрическая сумма ![]() , и наконец, умножив полученный вектор на множитель
, и наконец, умножив полученный вектор на множитель ![]() , получим искомый вектор
, получим искомый вектор ![]() .
.
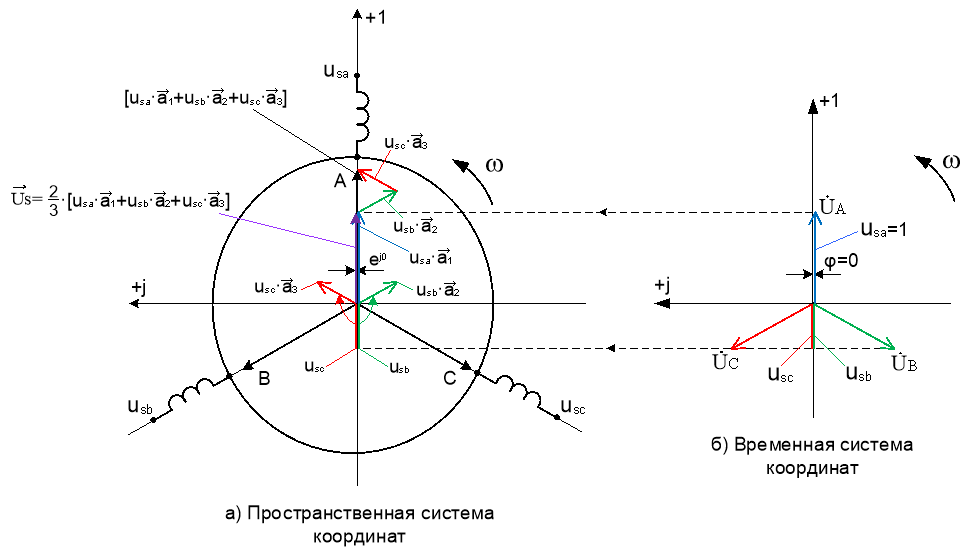
Рис. 1. Геометрический смысл построения пространственного вектора ![]() по составляющим
по составляющим ![]() ,
, ![]() и
и ![]()
Вектор тока статора ![]() :
:
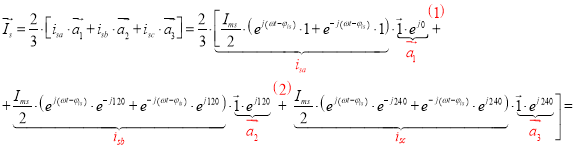
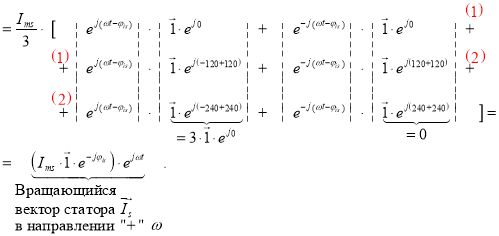
Вектор тока ротора ![]() :
:

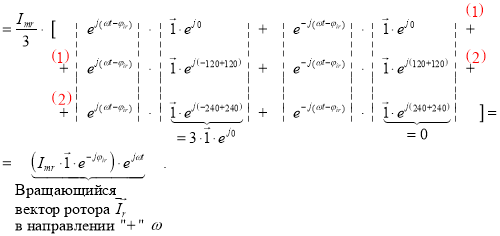
Вывод: пространственные векторы ![]() и
и ![]() сдвинуты на те же углы
сдвинуты на те же углы ![]() и
и ![]() в пространственной плоскости, что и соответствующие фазовые отставания φis и φir во времени по отношению к напряжению для фазы «а».
в пространственной плоскости, что и соответствующие фазовые отставания φis и φir во времени по отношению к напряжению для фазы «а».
3. Основные уравнения асинхронного двигателя в фазных переменных статора и ротора.
Обобщенная асинхронная машина показана на рис. 2.
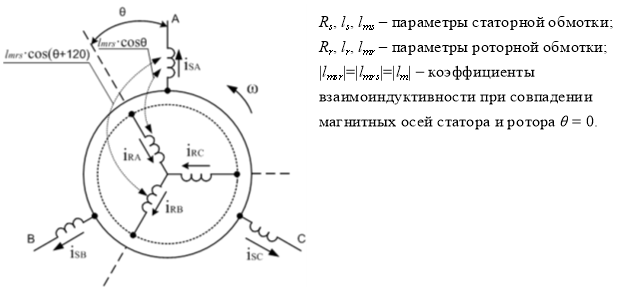
Рис. 2. Обобщённая асинхронная машина
Баланс фазных напряжений статорных и роторных цепей:
|
|
(5) |
|
(6) | |
|
(7) | |
|
(8) | |
|
(9) | |
|
(10) |
Потокосцепление фаз статорных и роторных цепей с учетом взаимоиндуктивностей с переменными коэффициентами, зависящими от расположения магнитных осей ротора и статора:
|
|
(11) |
|
(12) | |
|
(13) | |
|
(14) | |
|
(15) | |
|
(16) |
4. Преобразование балансов напряжений в фазных переменных в соответствующий баланс пространственных векторов.
Умножим обе части уравнения (5) на единичный пространственный вектор ![]() , уравнения (6) и (7) – соответственно на
, уравнения (6) и (7) – соответственно на ![]() и
и ![]() . Далее, просуммируем уравнения:
. Далее, просуммируем уравнения:
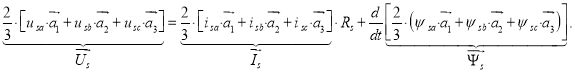
В векторной форме баланс напряжений для статора:
|
|
(17) |
Аналогично произведем преобразование баланса напряжений для роторных фазных переменных:
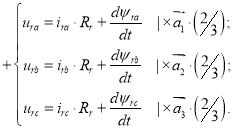
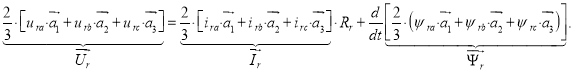
В векторной форме баланс напряжений для ротора:
|
|
(18) |
Литература:
- Пространственные векторы в асинхронном двигателе в относительной системе единиц / А. А. Емельянов, А. М. Козлов, В. В. Бесклеткин [и др.]. - Текст: непосредственный // Молодой ученый. - 2015. - № 11 (91). - С. 133-156.
- Ковач, К. П. Переходные процессы в машинах переменного тока / К. П. Ковач, И. Рац; пер. с нем. - Москва: Госэнергоиздат, 1963. - 735 c. - Текст: непосредственный.
- Шрейнер, Р. Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р. Т. Шрейнер, А. В. Костылев, В. К. Кривовяз, С. И. Шилин; под ред. проф. д.т.н. Р. Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 c. - Текст: непосредственный.
- Шрейнер, Р. Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты / Р. Т. Шрейнер. - Екатеринбург: УРО РАН, 2000. - 654 c. - Текст: непосредственный.