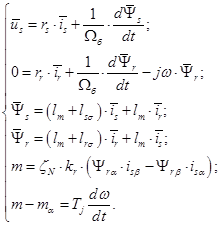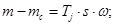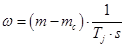Данная работа является продолжением опубликованной статьи [1], в которой были подробно показаны без сокращений способы и технологии получения пространственных векторов 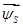 ,
, 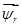 ,
, 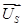 ,
, 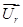 ,
, 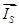 ,
, 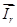 , в системе абсолютных едениц. Для неподвижной системы координат, основное уравнение в векторной форме переведены в систему относительных едениц.
, в системе абсолютных едениц. Для неподвижной системы координат, основное уравнение в векторной форме переведены в систему относительных едениц.
В работах [2; 3] приведено множество вариантов конечных результатов электромагнитного момента в зависимости от произведения проекций двух векторов 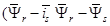 и т.д.). В этой статье сделан вывод одного из множества математических моделей асинхронного двигателя и сравнение полученных уравнений и структурной схемы с фундаментальной работой [3].
и т.д.). В этой статье сделан вывод одного из множества математических моделей асинхронного двигателя и сравнение полученных уравнений и структурной схемы с фундаментальной работой [3].
Система уравнений описывающих АД с короткозамкнутым ротором в неподвижной системе:
|
|
(1) |
|
(2) | |
|
(3) | |
|
(4) | |
|
(5) | |
|
(6) |
Так как электромагнитный момент определяется переменными 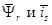 , то из системы уравнений (1) … (4) исключаем переменные
, то из системы уравнений (1) … (4) исключаем переменные 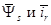 .
.
Из уравнения (4) выразим ток 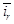 :
:
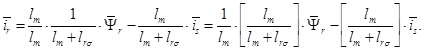
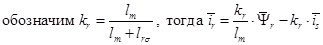 (7)
(7)
Далее, из уравнения (3) исключаем 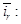
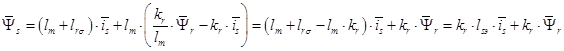 ,
,
где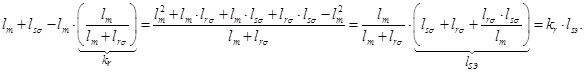
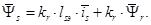 (8)
(8)
Из уравнения (2) исключаем переменную 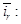
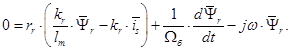 (9)
(9)
Выразим 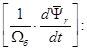
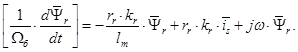 (10)
(10)
Из уравнения (9):
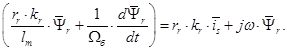
Переведем полученное уравнение из оригинала в изображение 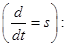
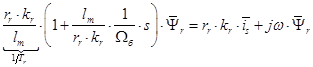 (11)
(11)
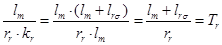
Умножим обе части уравнения (11) на 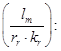
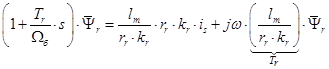
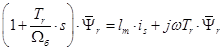 (12)
(12)
Разложим векторы по проекциям: 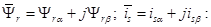
Подставим их в уравнение (12):
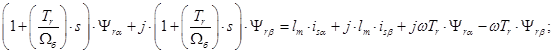 (13)
(13)
Проекция уравнения (13) на ось +1:
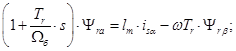 (14)
(14)
Проекция уравнения (14) на ось +j:
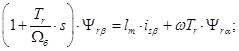 (15)
(15)
Из уравнения (14) определим 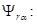
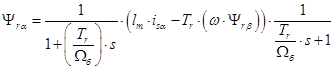 (16)
(16)
Уравнению (16) соответствует следующая структурная схема (рис. 1):
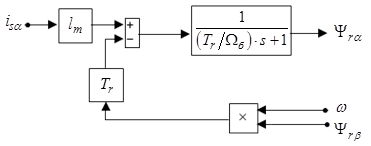
Рис. 1. Структурная схема для определения 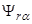 .
.
Из уравнения (15) определим 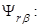
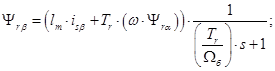 (17)
(17)
Уравнению (17) соответствует следующая структурная схема (рис. 2):
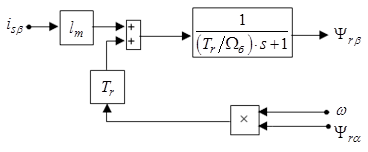
Рис. 2. Структурная схема для определения 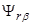 .
.
В уравнении (1) подставим 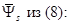
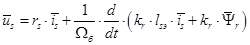
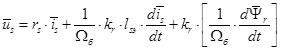
Подставим значение 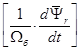 из уравнения (10):
из уравнения (10):
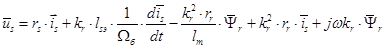
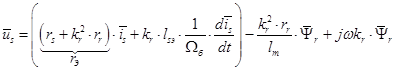
Переведем полученное уравнение из оригинала в изображение 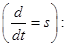
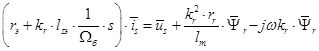
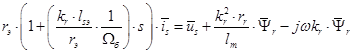
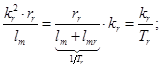
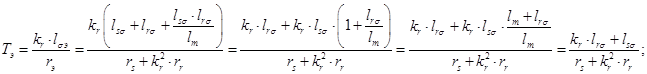
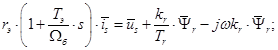 (18)
(18)
Разложим векторы по проекциям:
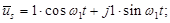
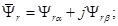
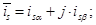
Подставим их в уравнение (18):
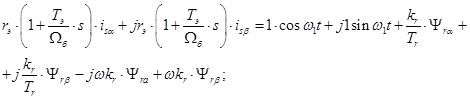 (*)
(*)
Проекция уравнения (*) на ось +1:
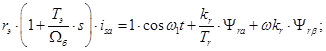 (19)
(19)
Проекция уравнения (*) на ось +j:
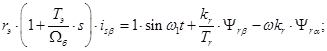 (20)
(20)
Из уравнения (19) выразим статорный ток 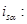
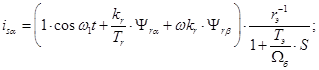 (21)
(21)
Уравнению (21) соответствует следующая структурная схема (рис. 3):
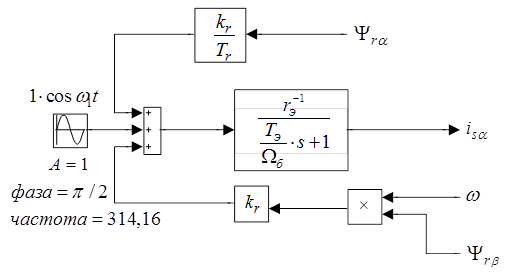
Рис. 3. Структурная схема для определения 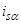 .
.
Из уравнения (20) выразим статорный ток 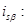
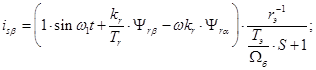 (22)
(22)
Уравнению (22) соответствует следующая структурная схема (рис. 4):
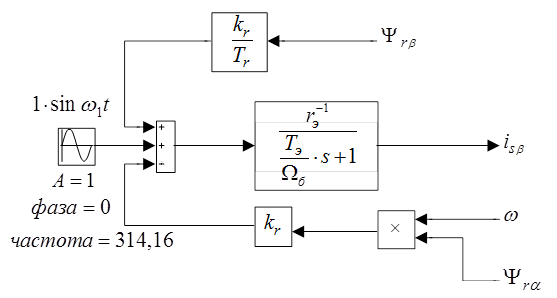
Рис. 4. Структурная схема для определения 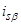 .
.
Электромагнитный момент определяется по формуле (5)
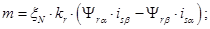 (**)
(**)
Структурная схема для реализации уравнения (5) дана на (рис. 5):
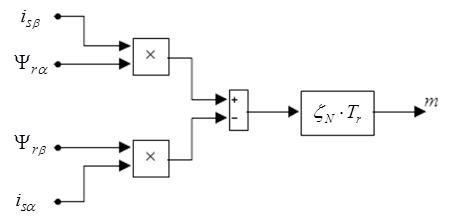
Рис. 5. Структурная схема для определения электромагнитного момента.
Наконец, для уравнения (6) структурная схема (рис. 6):
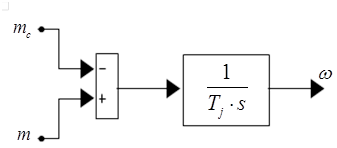
Рис. 6. Структурная схема для определения скорости.
В работе Шрейнера в главе 6 «Примеры» дан образец расчета параметров асинхронного двигателя. В наших дальнейших работах направленных на подготовку студентов к исследовательской работе, глава 6 окажет неоценимую помощь. Можно было бы по аналогии рассмотреть паспортные данные любого другого двигателя, но для проверки правильности выводов уравнений сделанных исследовательской группой самостоятельно, необходимо постоянно выходить на многие полученные результаты в работе [3]. Поэтому, этот пример рассчета окажется очень полезным.
Номинальные данные:
Номинальный режим работы S1;
Номинальная мощность 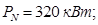
Номинальное фазное напряжение 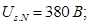
Номинальный фазный ток 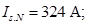
Номинальная частота 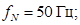
Номинальная синхронная скорость 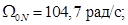
Номинальная скорость ротора 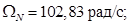
Номинальный КПД 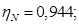
Номинальный коэффициент мощности 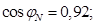
Число пар полюсов 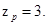
Параметры Т-образной схемы замещения при номинальной частоте:
Активное сопротивление обмотки статора 
Инуктивное сопротивления рассеяния обмотки статора 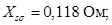
Активное сопротивление обмотки ротора, приведенное к статору 
Индуктивное сопротивление рассеяния обмотки ротора, приведенное статору 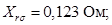
Главное индуктивное сопротивление 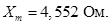
Базисные величины системы относительных единиц:
Напряжение 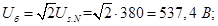
Ток 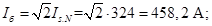
Частота 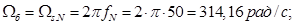
Скорость ротора 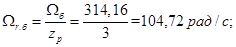
Сопротивление 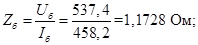
Потокосцепление 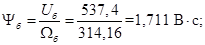
Индуктивность 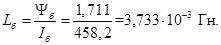
Используя номинальные данные двигателя, определяем:
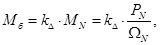
где 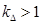 – коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (
– коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (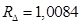 ).
).
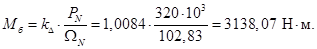
В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле:
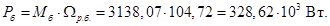
Относительные значения параметров схемы замещения двигателя:
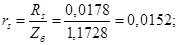
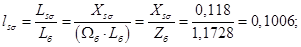
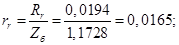
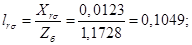
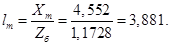
Механическая постоянная времени:
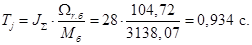
Номинальное значение скольжения:
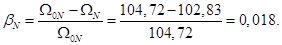
Относительное значение номинальной скорости ротора:
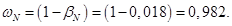
Нормирующий энергетический коэффициент:
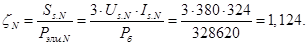
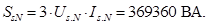
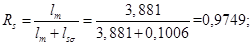
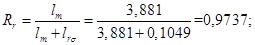
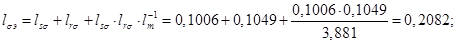
При расчете режимов работы, для того чтобы 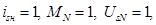
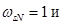
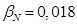 необходимо откорректировать
необходимо откорректировать 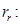
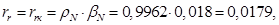
где 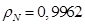 – корректирующий коэффициент [5, с. 296].
– корректирующий коэффициент [5, с. 296].
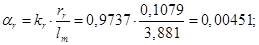
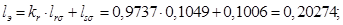
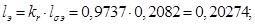
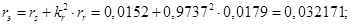
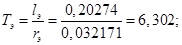
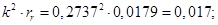
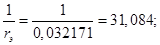
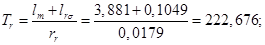
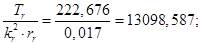
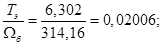
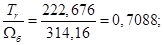
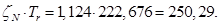
Математическая модель асинхронного двигателя в неподвижной системе координат представлена на рисунке 7. Результаты математического моделирования приведены на рисунках 8…10.
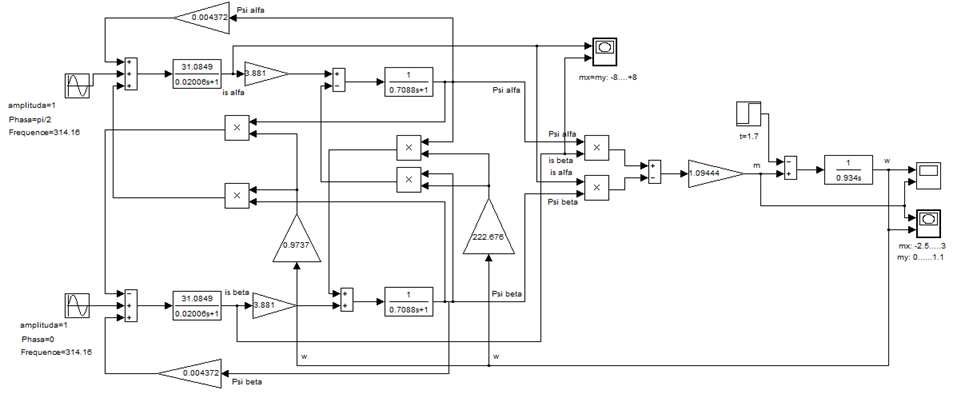
Рис. 7. Математическая модель асинхронного двигателя в неподвижной системе координат.
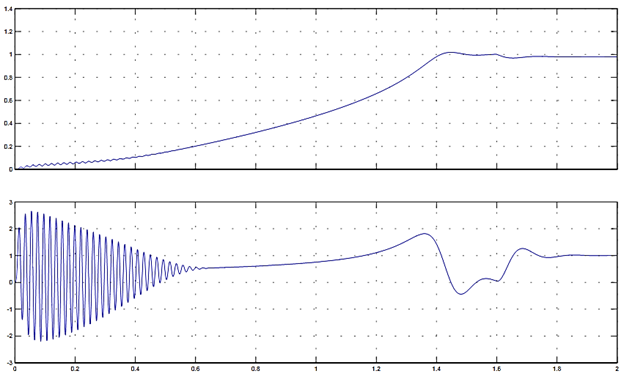
Рис. 8. Графики скорости и момента
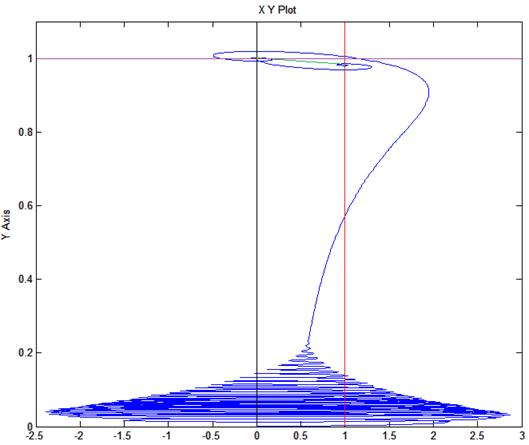
Рис. 9. Динамическая механическая характеристика при пуске и набросе нагрузки.
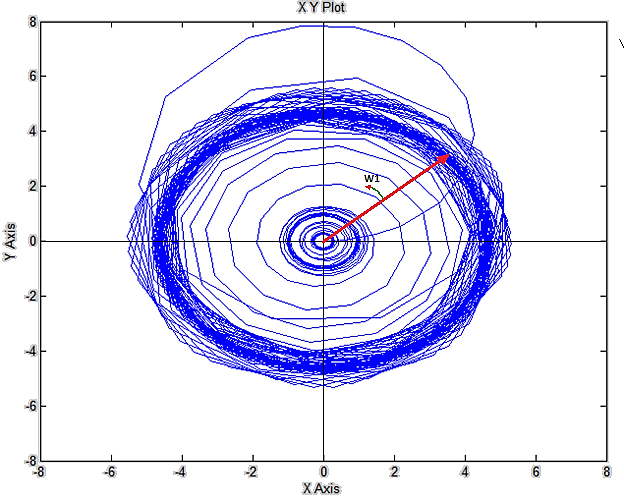
Рис. 10. Годограф вращающийся вектор тока статора в неподвижной системе координат.
Литература:
1. Пространственные векторы в асинхронном двигателе в относительной системе единиц// Молодой ученый. — 2015. — №11. — С. 133-156.
2. Шрейнер Р. Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления [Текст]: учеб. пособие / Р. Т. Шрейнер, А. В. Костылев, В. К. Кривовяз, С. И. Шилин. Под ред. проф. д.т.н. Р.Т.Шрейнера. Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т»., 2008. 361 с.
3. Шрейнер Р. Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты Екатеринбург УРО РАН, 2000. 654 с.
4. Математическая модель АД в неподвижной системе координат c переменными / А. А. Емельянов [и др.] // Молодой ученый. — 2010. — №3. Т.1. — С. 8-23.