Математическое моделирование САР скорости асинхронного двигателя с переменными ![]()
Емельянов Александр Александрович, доцент;
Бесклеткин Виктор Викторович, ассистент;
Авдеев Александр Сергеевич, студент;
Чернов Михаил Владимирович, студент;
Киряков Георгий Анатольевич, студент;
Габзалилов Эльвир Фиргатович, студент;
Российский государственный профессионально-педагогический университет (г. Екатеринбург)
При выполнении лабораторных работ по дисциплине «Системы управления электроприводов» необходимо, чтобы студенты имели представление о технологии моделирования многоконтурных систем управления асинхронным двигателем. Данная работа в доступной для студентов форме позволяет увидеть весь процесс моделирования начиная от математической модели двигателя и заканчивая настройкой регуляторов по току и скорости. Математическая модель двигателя была рассмотрена ранее в статье [1].
В контурах тока по проекциям x и y были получены одинаковые передаточные функции объектов управления:
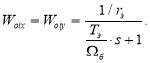
Синтез регуляторов тока производится по классической схеме [2]:
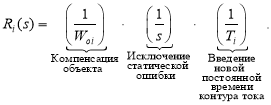
Передаточная функция фильтра:
![]()
Принимаем настройку на модульный оптимум ![]() , тогда передаточные функции регуляторов тока по проекциям x и y:
, тогда передаточные функции регуляторов тока по проекциям x и y:
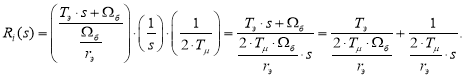
Обозначим:
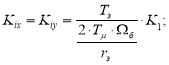
![]()
Фильтры в цепи задания тока (ФЗТ) и в цепи обратной связи (ФОТ), регулятор тока с пропорциональной ![]() и интегральной
и интегральной ![]() частями приведены на рис. 1 и 2.
частями приведены на рис. 1 и 2.
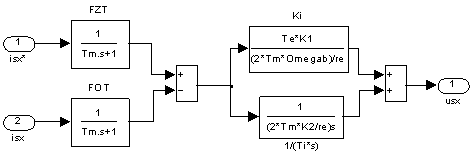
Рис. 1. Регулятор тока с ![]() и
и ![]() по проекции x
по проекции x
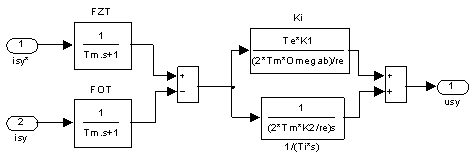
Рис. 2. Регулятор тока с ![]() и
и ![]() по проекции y
по проекции y
В работе предусмотрена компенсация внутренних перекрестных связей по току [5] (рис. 3).
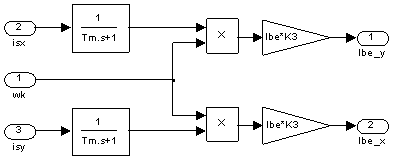
Рис. 3. Компенсация внутренних перекрестных связей
В контуре скорости передаточная функция объекта имеет следующий вид:
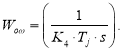
Синтез регулятора скорости:
![]()
где ![]()
Математическая модель регулятора скорости приведена на рис. 4.
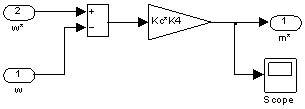
Рис. 4. Пропорциональный регулятор скорости
Задание по скорости формируется на Signal Builder и имеет следующую форму (рис. 5).
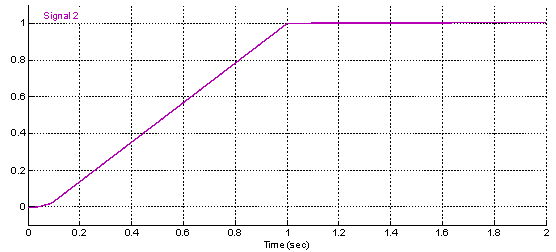
Рис. 5. Сигнал задания по скорости ω*
Номинальное потокосцепление ротора в соответствии с [3] определяется по следующей формуле и при векторном управлении поддерживается постоянным:
![]()
Задание на ток статора по проекции x определится по следующей формуле:
![]()
Математическая модель приведена на рис. 6.
![]()
Рис. 6. Реализация задания статорного тока ![]() по проекции x
по проекции x
Задание на статорный ток по проекции y:
![]()
Отсюда ![]()
Математическая модель определения ![]() дана на рис. 7.
дана на рис. 7.
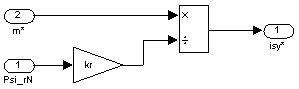
Рис. 7. Реализация статорного тока ![]() по проекции y
по проекции y
Скольжение системы координат и скорость её вращения определяются по следующим зависимостям [4]:
![]()
![]()
Математическая модель определения угловой скорости вращения координатной системы приведена на рис. 8.
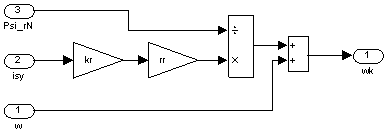
Рис. 8. Реализация определения ![]() в Matlab
в Matlab
Математическая модель оболочки асинхронного двигателя с переменными ![]() дана на рис. 9.
дана на рис. 9.

Рис. 9. Модель оболочки АД с переменными ![]() в Simulink-Matlab
в Simulink-Matlab
Расчет параметров двигателя в Simulink представлен на рис. 10.

Рис. 10. Расчет коэффициентов по паспортным (справочным) данным
Определение коэффициентов оболочки двигателя дано на рис. 11.
Полная схема математической модели САР скорости асинхронного двигателя приведена на рис. 12.

Рис. 11. Определение коэффициентов оболочки АД в Simulink-Matlab

Рис. 12. Полная схема математической модели САР скорости АД
В работе [3] в главе 6 «Примеры» дан образец расчета параметров асинхронного двигателя. В наших дальнейших работах направленных на подготовку студентов к исследовательской работе, глава 6 окажет неоценимую помощь. Можно было бы по аналогии рассмотреть паспортные данные любого другого двигателя, но для проверки правильности выводов уравнений сделанных исследовательской группой самостоятельно, необходимо постоянно выходить на многие полученные результаты в работе [4]. Поэтому, этот пример расчета окажется очень полезным.
Номинальные данные:
Номинальный режим работыS1;
Номинальная мощность![]()
Номинальное фазное напряжение![]()
Номинальный фазный ток![]()
Номинальная частота.![]()
Номинальная синхронная скорость![]()
Номинальная скорость ротора![]()
Номинальный КПД![]()
Номинальный коэффициент мощности![]()
Число пар полюсов![]()
Параметры Т-образной схемы замещения при номинальной частоте:
Активное сопротивление обмотки статора![]()
Индуктивное сопротивление рассеяния обмотки статора![]()
Активное сопротивление обмотки ротора, приведенное к статору![]()
Индуктивное сопротивление рассеяния обмотки ротора, приведенное статору![]()
Главное индуктивное сопротивление![]()
Суммарный момент инерции двигателя и механизма![]()
Базисные величины системы относительных единиц:
Напряжение![]()
Ток![]()
Частота![]()
Скорость ротора![]()
Сопротивление![]()
Потокосцепление![]()
Индуктивность![]()
Используя номинальные данные двигателя, определяем:
![]()
где ![]() – коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (
– коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (![]() ).
).
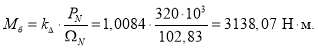
В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле:
![]()
Относительные значения параметров схемы замещения двигателя:
![]()
![]()
![]()
![]()
![]()
Механическая постоянная времени:
![]()
Номинальное значение скольжения:
![]()
Относительное значение номинальной скорости ротора:
![]()
Нормирующий энергетический коэффициент:
![]()
![]()
![]()
![]()
![]()
При расчете режимов работы, для того чтобы ![]()
![]()
![]()
![]() и
и ![]() необходимо откорректировать
необходимо откорректировать ![]()
![]()
где ![]() – корректирующий коэффициент [3, с. 296].
– корректирующий коэффициент [3, с. 296].
![]() - коэффициент, показывающий отношение
- коэффициент, показывающий отношение ![]() к
к ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Расчет этих коэффициентов производим в Script:
%Номинальные данные
PN=320000;
UsN=380;
IsN=324;
fN=50;
Omega0N=104.7;
OmegaN=102.83;
nN=0.944;
cos_phiN=0.92;
zp=3;
%Параметры Т-образной схемы замещения при номинальной частоте
Rs=0.0178;
Xs=0.118;
Rr=0.0194;
Xr=0.123;
Xm=4.552;
J=28;
%Базисные величины системы относительных единиц
Ub=sqrt(2)*UsN;
Ib=sqrt(2)*IsN;
OmegasN=2*pi*fN;
Omegab=OmegasN;
Omegarb=Omegab/zp;
Zb=Ub/Ib;
Psib=Ub/Omegab;
Lb=Psib/Ib;
kd=1.0084;
Mb=kd*PN/OmegaN;
Pb=Mb*Omegarb;
rs=Rs/Zb;
ls=Xs/Zb;
lr=Xr/Zb;
lm=Xm/Zb;
Tj=J*Omegarb/Mb;
betaN=(Omega0N-OmegaN)/Omega0N;
wN=(1-betaN);
SsN=3*UsN*IsN;
zetaN=SsN/Pb;
ks=lm/(lm+ls);
kr=lm/(lm+lr);
lbe=ls+lr+ls*lr*lm^(-1);
roN=0.9962;
rr=roN*betaN;
alphar=kr*rr/lm;
le=kr*lbe;
re=rs+(kr^2)*rr;
Te=le/re;
Tr=(lm+lr)/rr;
Psi_rN=0.942;
Tm=0.005;
Результаты расчетов скорости ω и электромагнитного момента m при ![]()
![]()
![]()
![]() приведены на рис. 13.
приведены на рис. 13.
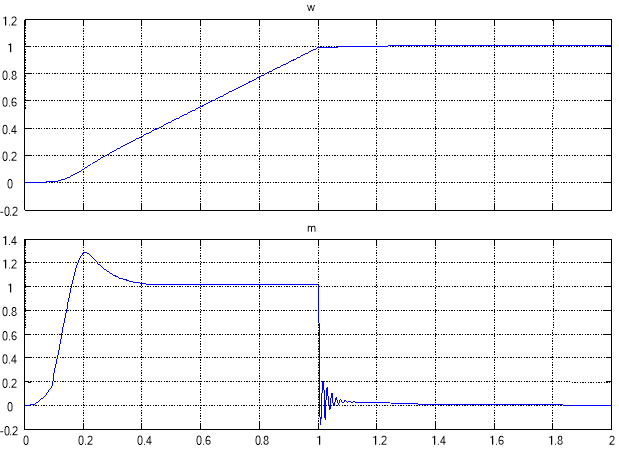
Рис. 13. Графики скорости и момента
Литература:
-
Емельянов А.А., Бесклеткин В.В., Авдеев А.С., Чернов М.В., Киряков Г.А., Габзалилов Э.Ф., Фуртиков К.А., Реутов А.Я., Королёв О.А. Математическая модель асинхронного двигателя с переменными
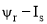 в произвольной системе координат на основе интегрирующих звеньев // Молодой ученый. — 2015. — № 15 (95). — С. 7-30.
в произвольной системе координат на основе интегрирующих звеньев // Молодой ученый. — 2015. — № 15 (95). — С. 7-30.
- Шрейнер Р.Т. Системы подчиненного регулирования электроприводов: учеб. пособие / Р.Т. Шрейнер. - Екатеринбург: Изд-во ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. – 279 с.
- Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.
- Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. - 654 с.
- Шрейнер Р.Т. Электроприводы переменного тока на базе непосредственных преобразователей частоты с ШИМ: монография / Р.Т. Шрейнер, А.И. Калыгин, В.К. Кривовяз; под. ред. Р.Т. Шрейнера. - Екатеринбург: ФГАОУ ВПО «Рос. гос. проф.-пед. ун-т», 2012. – 223 с.

